AbelFactorial

$y=\mathrm{AbelFactorial}(x)$ and $y=\mathrm{ArcFactorial}(x)$ versus $x$

Map of $f = \mathrm{AbelFactorial}(x+\mathrm i y)$ in the $x$,$y$ plane shown with isolines $p\!=\!\Re(f)\!=$const and $q\!=\!\Im(f)\!=$const

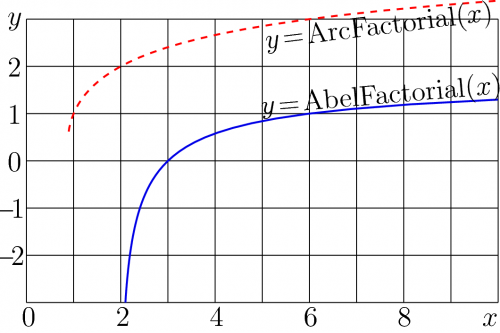
AbelFactorial is holomorphic function, inverse of the SuperFactorial, Abel function of Factorial constructed with regular iteration at its fixed points 2 in such a way that

$\mathrm{AbelFactorial}(z^*)=\mathrm{AbelFactorial}(z)^*$.

$\mathrm{AbelFactorial}(3)=0$

$\displaystyle

\lim_{x\rightarrow -\infty}\mathrm{AbelFactorial}(x+\mathrm i y)=2 ~ ~ \forall y \in \mathbb R: y\!\ne\!0$

Along the real axis, AbelFactorial is slowly growing function, its growth is much slower than that of ArcFactorial shown in the top figure at right.

ArcFactorial is analytic in the complex plane with cut in the direction of the negative part f the real axis; the range of holomorphizm is $\mathbb C \backslash \{ x\in \mathbb{R}: x\le 2\}$.

Abel equation

AbelFactorial $G$ satisfies the Abel equation

(1) $~ ~ ~ G(z!)=G(z)+1$

The Abel equation is consistent with the transfer equation for the SuperFactorial $F=G^{-1}$:

(2) $~ ~ ~ \mathrm{Factorial}(F(z))=F(z\!+\!1)$

Regular iteration

For the evaluation of AbelFactorial, the regular iteration at the fixed point 2 of factorial is efficient. The following expansion is suggested :

(2) $~ ~ ~

\tilde G(z)= \frac{1}{k} \log\!\left(\sum_{n=1}^{N-1}U_{n}(z\!-\!2)^{n}+\mathcal{O}(z\!-\!2)^N\right) $ where

(3) $~ ~ ~ k=\ln\!\big(3+2\!~\mathrm{Factorial}^{\prime}(0)\big)=\ln(3-2\!~\gamma)

\approx 0.6127874523307$, $\gamma$ is the Euler's constant;

$U_1 =1$

$U_{2}=-\frac{\pi^2+6\gamma^{2}-18\gamma+6}{12(3-5\gamma+2\gamma^{2})}

\approx 0.798731835$

The coefficients $U$ can be found substituting the representation (2) into the Abel equation (1) and expanding the result to the power series with small parameter $z\!-\!2$.

Extension of the regular iteration

If $|z\!-\!2|$ is not small, then the representation

(4) $~ ~ ~ \tilde G(z)=\tilde G (\mathrm{ArcFactorial}^n(z))+n$

can be be used for integer $n$.

The AbelFactorial $G$ can be expressed through $\tilde{G}$;

(5) $~ ~ ~ G(z)=\tilde G(z) - \tilde G(3)$

in such a way that $G(3)=0$, corresponding to $\mathrm{SuperFactorial}(0)=3$.

Previous notation

In publication , function $\tilde G$ is called "ArcSuperFactorial" and denoted with letter $G$; however, it is more convenient to deal with a function that takes integer values at least for some integer values of the argument; therefore the representation (5) is recommended.

Iteration of Factorial

Together with Superfactorial $F=G^{-1}$, the AbelFactorial $G$ allow to express the $c$-th iteration of Factorial as follows:

(6) $~ ~ ~

\mathrm{Factorial}^c(z)= F(c+G(z))$ where $c$ has no need to be integer. In particular,
at $c=1$, $~ \mathrm{Factorial}^c(z)=z!$;
at $c=0$, $~ \mathrm{Factorial}^c(z)=z$;
at $c=-1$, $~ \mathrm{Factorial}^c(z)=\mathrm{ArcFactorial}(z)$;
and at $c=1/2$, such a representation determines the square root of factorial, id est, $\sqrt{!\,}$, that is used as Logo of the Physics Department of the Moscow State University and part of logo of TORI shown in the left top corner of each page of TORI. In some facility of the half-line $z\!>\!2$, the following relation holds

(7) $~ ~ ~

\sqrt{!\,} \Big( \sqrt{!\,}\big(z\big)\Big)= z! $