Difference between revisions of "Acosq"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
[[File:AcosqplotT100.png|500px|right]] |
[[File:AcosqplotT100.png|500px|right]] |
||
| − | '''Acosq''' or '''acosq''' or '''[[ArcCosq]]''' is expressed through [[ArcCosc]] of argument rotated for the '''Q'''uater of |
+ | '''Acosq''' or '''acosq''' or '''[[ArcCosq]]''' is expressed through [[ArcCosc]] of argument rotated for the '''Q'''uater of \(\pi\) phase, id est |
| − | : |
+ | : \(\mathrm{acosq}(z)=\mathrm{acosc}\left( \mathrm e ^{\mathrm i \pi/4} \,z \right)\) |
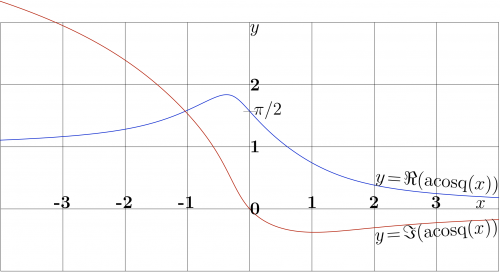
Behavior of [[acosq]] along the real axis is shown in the figure at right; |
Behavior of [[acosq]] along the real axis is shown in the figure at right; |
||
| Line 80: | Line 80: | ||
\put(4,6){\ing{acosqplot}} %<br> |
\put(4,6){\ing{acosqplot}} %<br> |
||
%\put(4,6){\ing{sazaecon}} %<br> |
%\put(4,6){\ing{sazaecon}} %<br> |
||
| − | \put(416,402){\sx{2.5}{ |
+ | \put(416,402){\sx{2.5}{\(y\)}} %<br> |
\put(416,308){\sx{2.4}{\bf 2}} %<br> |
\put(416,308){\sx{2.4}{\bf 2}} %<br> |
||
| − | \put(422,269){\sx{2.4}{ |
+ | \put(422,269){\sx{2.4}{\(\pi/2\)}} %<br> |
\put(416,208){\sx{2.4}{\bf 1}} %<br> |
\put(416,208){\sx{2.4}{\bf 1}} %<br> |
||
%\put(16,160){\sx{1.8}{\bf 2.5}} %<br> |
%\put(16,160){\sx{1.8}{\bf 2.5}} %<br> |
||
| Line 97: | Line 97: | ||
\put(708, 118){\sx{2.4}{\bf 3}} %<br> |
\put(708, 118){\sx{2.4}{\bf 3}} %<br> |
||
%\put(807, 120){\sx{2.2}{\bf 4}} %<br> |
%\put(807, 120){\sx{2.2}{\bf 4}} %<br> |
||
| − | %\put(161, 132){\sx{2.8}{ |
+ | %\put(161, 132){\sx{2.8}{\(\frac{\pi}{2}\)}} %<br> |
| − | %\put(471, 130){\sx{2.6}{ |
+ | %\put(471, 130){\sx{2.6}{\(\frac{3\pi}{2}\)}} %<br> |
| − | \put(780, 118){\sx{2.4}{ |
+ | \put(780, 118){\sx{2.4}{\(x\)}} %<br> |
| − | \put(618,160){\sx{2.52}{\rot{-4} |
+ | \put(618,160){\sx{2.52}{\rot{-4}\(y\!=\!\Re(\mathrm{acosq}(x))\)\ero}} %<br> |
| − | \put(618, 65){\sx{2.52}{\rot{4} |
+ | \put(618, 65){\sx{2.52}{\rot{4}\(y\!=\!\Im(\mathrm{acosq}(x))\)\ero}} %<br> |
\end{picture} %<br> |
\end{picture} %<br> |
||
} %<br> |
} %<br> |
||
Latest revision as of 18:25, 30 July 2019
Acosq or acosq or ArcCosq is expressed through ArcCosc of argument rotated for the Quater of \(\pi\) phase, id est
- \(\mathrm{acosq}(z)=\mathrm{acosc}\left( \mathrm e ^{\mathrm i \pi/4} \,z \right)\)
Behavior of acosq along the real axis is shown in the figure at right; graphic of real part is shown with blue curve, that of imaginary part is shown with red curve.
ArcCosc is used in the expression of the effective transversal wavenumber of the principal mode at the guiding of atoms between absorbing walls. However, the same function describes that for any other kinds of waves.
C++ generator of curves
Files ado.cin and acosc.cin should be loaded in the working directory for the compilation of the C++ code below
#include <math.h> #include <stdio.h> #include <stdlib.h> #define DB double #define DO(x,y) for(x=0;x<y;x++) using namespace std; #include <complex> typedef complex<double> z_type; #define Re(x) x.real() #define Im(x) x.imag() #define I z_type(0.,1.) #include "ado.cin" //#include "acip.cin"
#include "acosc.cin"
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
#define S(x,y) fprintf(o,"S\n",);
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
DB Sazae= 2.798386045783887; // H
DB Tarao= -0.33650841691839534; // J
FILE *o;o=fopen("acosqplot.eps","w");ado(o,820,460);
fprintf(o,"410 110 translate\n 100 100 scale\n");
for(m=-4;m<5;m++){M(m,-1)L(m,3)}
for(n=-1;n<4;n++){M(-4,n)L(4,n)}
fprintf(o,"2 setlinecap .005 W 0 0 0 RGB S\n");
/*
for(m=-4;m<3;m++){M(.5+m,-1)L(.5+m,3)}
for(n=-1;n<3;n++){M(-4,n+.5)L(4,n+.5)}
fprintf(o,"2 setlinecap .003 W 0 0 0 RGB S\n");
*/
DO(m,802){x=-4.01+.01*m; z=x*exp(.25*M_PI*I); y=Re(acosc(z)); if(m==0)M(x,y)else L(x,y) }
fprintf(o,"1 setlinejoin 1 setlinecap .01 W 0 0 .8 RGB S\n");
DO(m,802){x=-4.01+.01*m; z=x*exp(.25*M_PI*I); y=Im(acosc(z)); if(m==0)M(x,y)else L(x,y) }
fprintf(o,"1 setlinejoin 1 setlinecap .01 W .8 0 0 RGB S\n");
M(-.1,M_PI/2)L( .1,M_PI/2) fprintf(o,".004 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf acosqplot.eps");
system( "open acosqplot.pdf");
getchar(); system("killall Preview");//for mac
}
Latex generator of labels
% File asocqplot.pdf sould be generated with the code above in order to compile the Latex document below.
%<br> % Copyleft 2012 by Dmitrii Kouznetsov %<br> \documentclass[12pt]{article} %<br> \usepackage{geometry} %<br> \usepackage{graphicx} %<br> \usepackage{rotating} %<br> \paperwidth 1612pt %<br> \paperheight 878pt %<br> \topmargin -90pt %<br> \oddsidemargin -106pt %<br> \textwidth 900pt %<br> \textheight 900pt %<br> \pagestyle {empty} %<br> \newcommand \sx {\scalebox} %<br> \newcommand \rot {\begin{rotate}} %<br> \newcommand \ero {\end{rotate}} %<br> \newcommand \ing {\includegraphics} %<br> \begin{document} %<br> \parindent 0pt \sx{2}{ \begin{picture}(840,444) %<br> \put(4,6){\ing{acosqplot}} %<br> %\put(4,6){\ing{sazaecon}} %<br> \put(416,402){\sx{2.5}{\(y\)}} %<br> \put(416,308){\sx{2.4}{\bf 2}} %<br> \put(422,269){\sx{2.4}{\(\pi/2\)}} %<br> \put(416,208){\sx{2.4}{\bf 1}} %<br> %\put(16,160){\sx{1.8}{\bf 2.5}} %<br> %\put(16, 262){\sx{2.2}{Wakame}} %<br> \put(416,108){\sx{2.4}{\bf 0}} %<br> %\put(16, 75){\sx{2.4}{Tarao}} %<br> \put(100, 118){\sx{2.4}{\bf -3}} %<br> \put(200, 118){\sx{2.4}{\bf -2}} %<br> \put(300, 118){\sx{2.4}{\bf -1}} %<br> \put(508, 118){\sx{2.4}{\bf 1}} %<br> %\put(142,120){\sx{2.4}{\rot{90}Fune\ero}} %<br> \put(608, 118){\sx{2.4}{\bf 2}} %<br> %\put(302,118){\sx{2.5}{\rot{90}Sazae\ero}} %<br> \put(708, 118){\sx{2.4}{\bf 3}} %<br> %\put(807, 120){\sx{2.2}{\bf 4}} %<br> %\put(161, 132){\sx{2.8}{\(\frac{\pi}{2}\)}} %<br> %\put(471, 130){\sx{2.6}{\(\frac{3\pi}{2}\)}} %<br> \put(780, 118){\sx{2.4}{\(x\)}} %<br> \put(618,160){\sx{2.52}{\rot{-4}\(y\!=\!\Re(\mathrm{acosq}(x))\)\ero}} %<br> \put(618, 65){\sx{2.52}{\rot{4}\(y\!=\!\Im(\mathrm{acosq}(x))\)\ero}} %<br> \end{picture} %<br> } %<br> \end{document} %
Keywords
ArcCosc, Cosc, Sazae-san functions, Guiding of waves between absorbing walls