ArcCosc
ArcCosc denoted aslo as acosc is inverse function of Cosc defined with
- \( \displaystyle \mathrm{cosc}(z)=\frac{\cos(z)}{z}\)
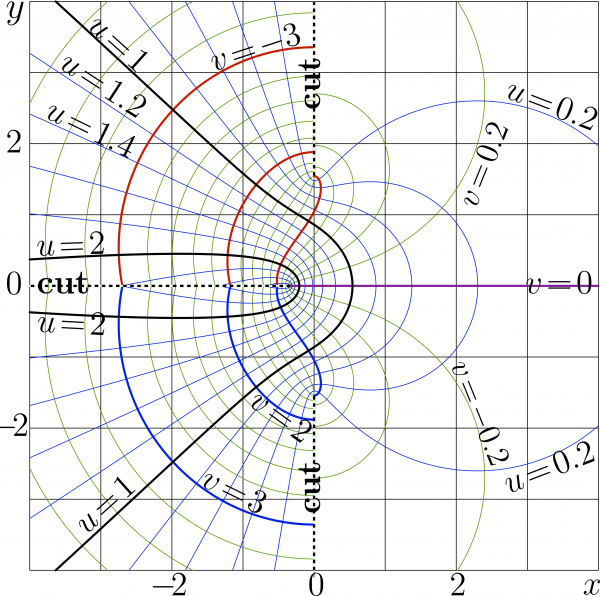
ArcCosc appears in the calculation of mode of wave channeled between absorbing walls. However, it may have also other applications. Tterefore, the robust C++ implementation is supplied in the description of the complex map (click on the map at right).
History and ethimology
The previous version of this article uses name ArcCip instead of ArcCosc. Then it happened that the inverse function of sinc has similar application (for antisymmetric mode);
- \(\displaystyle \mathrm{sinc}(z)=\frac{\sin(z)}{z}\)
Function sinc already has well established name [1][2]. For this analogy, the name of function Cosc is used. As usually, the name of the inverse function is created adding prefic Arc or a.
For this reason the function is called ArcCosc.
Notations
In formulas, the old name ArcCip and the short name acosc also may be used.
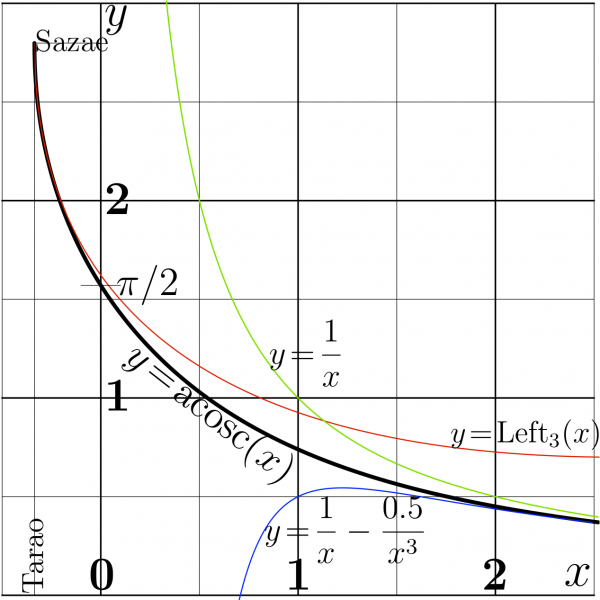
The first real extremum of function cosc is denoted with name Sazae; its value is denoted with name Tarao:
- \(\mathrm{cosc}(\mathrm{Sazae})=\mathrm{Tarao}~\) , \(~ ~ \mathrm{cosc}'(\mathrm{Sazae})=0\)
- \(\mathrm{Sazae} \approx ~ 2.798386045783887\)
- \(\mathrm{Tarao} \approx\! -0.33650841691839534\)
- \(\mathrm{acosc}(\mathrm{Tarao})=\mathrm{Sazae}\)
In the figure with the explicit plot of acosc, it is compared with its asymptotic denoted with name \(\mathrm{Left}_3\).
- \(\displaystyle \mathrm{Left}_3(z)=\mathrm{Sazae} - \Bigg( \frac{2(z\!-\!\mathrm{Tarao})} {- \mathrm{Tarao} } \Bigg)^{\!\!1/2} - \frac{2 (z\! -\!\mathrm{Tarao})} {3 ~\rm Sazae~Tarao} \)
The subscript 3 indicates that the only 3 terms taken into account in the expansion. Function \(\mathrm{Left}_3(z)\) approximates \(\mathrm{acosc}(z)\) in the left hand side of the figure;
- \(\displaystyle \mathrm{acosc}(z)= \mathrm{Left}_3(z) + O(z -\mathrm{Tarao})^{3/2}\)
ArcCosc of real argument
Along the real axis, ArcCosc is defined for argument not smaller than
- \(\mathrm{Tarao} \approx -0.33650841691839534\)
AcrCosc is monotonously decreasing function, it decreases from value Sazae at Tarao till zero at \(+\infty\).
- \(\mathrm{acosc}(\mathrm{Tarao}) = \mathrm{Sazae} \approx 2.798386045783887\)
At Tarao, ArcCosc has singularity (branch point), its derivative becomes infinite.
Specific value ArcCosc has at zero,
- \(\mathrm{acosc}(0)= \pi/2 \approx 1.5707963267948966\)
The expansion of ArcCosc at zero has form
- \(\displaystyle \mathrm{acosc}(z)= \frac{\pi}{2} - \frac{\pi}{2} z + \frac{\pi}{2} z^2 - \frac{\pi ~ (24\!+\!\pi^2)}{48} z^3 + \frac{\pi ~ (6\!+\!\pi^2)}{12} z^4 +...\)
Mathematica built-in operation InverseSeries allows straightforward calculation of many terms of this expansion. The radius of convergence of this series, id est, \(- \mathrm{Tarao}\), is determined by the distance to the closest singularity.
At infinity, ArcCosc decays becomming almost inversly proportional to its arument.
Few asymptotics of ArcCosc are shown in the figure.
More expansions of ArcCosc
In vicinity of Tarao, ArcCosc can be approximated with series
- \(\!\!\!\!\!\!\!\!\!\! \displaystyle \mathrm{acosc}(\mathrm{Tarao}\!+\!t)=\mathrm{Sazae} -\Bigg(\frac{- 2 ~ t}{\mathrm{Tarao}}\Bigg)^{\! 1/2} + \frac{2 ~ t}{\mathrm{Sazae} ~ \mathrm{Tarao}} - \frac{3~\mathrm{Sazae}^2-4}{9~ \mathrm{Sazae}^2} \Bigg( \frac{- ~ t}{2~ \mathrm{Tarao}} \Bigg)^{3/2} + ..\)
The truncated series with tree terms gives approximation called \(\mathrm{Left}_3\) shown at the figure; it approximates ArcCosc at the left hand side of the figure.
Similar expansion can be written for the point named i Wakame; Wakame is real solution of equation
- \(\mathrm{cosc}'(\mathrm{i} ~ \mathrm{Wakame})=0\)
- \(\mathrm{Wakame} \approx 1.50887956153832\)
- \(\mathrm{cosc}(\mathrm{i} ~ \mathrm{Wakame})= - \mathrm{i} ~ \mathrm{Fune} \approx - \mathrm{i} ~ 1.199678640257734\)
For calculations and evaluation of the coefficients of this expansion, it is convenient to deal with function ArcCohc, which is inverse function of
- \( \displaystyle \mathrm{cohc}(z)=\frac{ \cosh(z) }{z}= - \mathrm{i}~ \mathrm{cosc}(\mathrm{i} z)\)
A dozen terms of these expansions can be calculated with Mathematica. The radius \(r\) of convergence of these series is determined by the distance to the nearby singularity, \(r=\sqrt{\mathrm{Tarao}^2+\mathrm{Wakame}^2} \approx 1.5459480734762723\)
At Infinity, ArcCosc can be expanded as follows
- \(\displaystyle \mathrm{acosc}(z) = \frac{1}{z}-\frac{1}{2 z^3}+\frac{13}{24 z^5}-\frac{541}{720 z^7}+\frac{9509}{8064 z^9} + ..\)
This expansion can be used for the precise approcimation of ArcCosc while \(|z|\gg 1\), \(\Re(z)\!>\!0 \).
Numerical implementation
The C++ implementation with complex double precision is available in the descriptions of the figures (Just click at the picture).
The expansions of the function at its branch points is used to get the primary approximation, then the value is adjusted with the Newton algorithm.
The bransh points are Tarao, \(\mathrm{i}\,\mathrm{Wakame}\) and \(-\mathrm{i}\,\mathrm{Wakame}\), where
- \( \mathrm{Wakame}=\mathrm{cohc}(\mathrm{Fune})\)
Name Fune is used for the real solution of equation
- \( \mathrm{cohc}'( \mathrm {Fune} )=0\)
where
- \( \displaystyle \mathrm{cohc}(z)= \frac{\cosh(z)}{z}\)
Constants Wakame and Fine have the following values:
- \( \mathrm{Wakame} \approx 1.50887956153832\)
- \( \mathrm{Fune} \approx 1.199678640257734\)
in such a way,
- \( \mathrm{Fune} = \mathrm{acohc}(\mathrm{Wakame})\)
where acohc=ArcCohc is inverse function of cohc.
For the rough approximation of \(\mathrm{acosc}(z)\), first, one of the four expansions mentioned above is used: at Tarao, at \(\pm \mathrm i \, \mathrm{Wakame}\) and at \(+\infty~\). Then the approximation \(s_0\) is adjusted with the Newton algorithm,
- \(\displaystyle s_{n+1}=s_n+ \frac{z-\mathrm{cosc}(s_n)}{ \mathrm{cosc}'(s_n)}\)
While there exist efficient implementations of \(\mathrm{cosc}\) and \(\mathrm{cosc}'\), it is faster to make few additional iterations than to increase number of terms in the truncated series of the primary approximation; the goal of the primary approximation is to indicate the correct branch of the inverse function. Then, the Newtom method converges quickly: from 4 to 7 iterations are applied giving at least 14 correct decimal digits in the result.
Constants
Four mathematical constants are defined above. In order to avoid confusions with single–letter notations, for these constants the following names are suggested: Sazae, Tarao, Fune, Wakame.
- \(\mathrm{Sazae} \approx ~ 2.798386045783887\)
- \(\mathrm{Tarao} \approx\! -0.33650841691839534\)
- \( \mathrm{Fune} \approx 1.199678640257734\)
- \( \mathrm{Wakame} \approx 1.50887956153832\)
with the following properties:
- \( \mathrm{cosc}'(\mathrm{Sazae}) =0\)
- \( \mathrm{cosc}(\mathrm{Sazae}) =\mathrm{Tarao}\)
- \( \mathrm{acosc}(\mathrm{Tarao}) =\mathrm{Sazae}\)
- \( \mathrm{cohc}'(\mathrm{Fune}) =0\)
- \( \mathrm{cohc}(\mathrm{Fune}) =\mathrm{Wakame}\)
- \( \mathrm{acohc}(\mathrm{Wakame}) =\mathrm{Fune}\)
Knowledge of these constants simplifies evaluation of functions ArcCosc and ArcCohc.
Conclusion
The knowledhe of the asymptotic behavior and the high efficiency of the evaluation algorithm allows to deal with ArcCosc as it it would be elementary function. It has sense to include such functions as Tetration, ArcTetration, SuperFactorial, AbelFactorial, and ArcCosc to the set of Special functions.
See also
cos, ArcCos, acosq, Sinc, complex map, inverse function