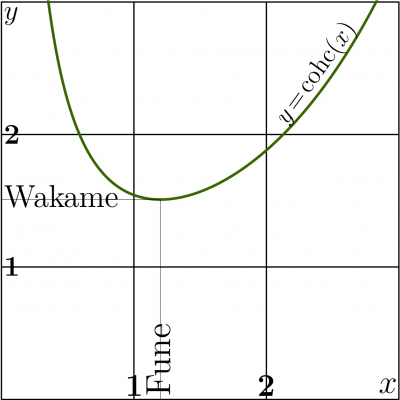
Wakame
Wakame is real number, value of function cohc at its minimum Fune and singularity of function ArcCohc at the real axis;
- \(\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ ~ \mathrm{Wakame}\approx 1.50887956153832\)
Wakame appears as value of function Cohc at its extremum, called Fune:
- \(\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ ~ \mathrm{cohc}( \mathrm{Fune})=\mathrm{Wakame}\)
- \(\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ ~ \mathrm{cohc}'(\mathrm{Fune})=0\)
where cosc=Cohc is elementary function ;
- \(\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ ~ \mathrm{cohc}(z)=\frac{\cosh(z)}{z}\);
- \(\!\!\!\!\!\!\!\!\! (5) ~ ~ ~ ~ \mathrm{cohc}'(z)=\frac{\sinh(z)}{z}-\frac{\cosh(z)}{z^2}\)
The numerical solution of the equation (3) gives the approximation
- \(\!\!\!\!\!\!\!\!\! (6) ~ ~ ~ ~ \mathrm{Fune} \approx 1.199678640257734\)
With the inverse function of cosc, Fune can be expressed through Wakame,
- \(\!\!\!\!\!\!\!\!\! (7) ~ ~ ~ ~ \mathrm{Fune}= \mathrm{acohc}(\mathrm{Wakame})\)
The expansion of function cohc at Fune is used for the expansion of function ArcCohc at Wakame in the numerical implementation of function . Also, point \(\mathrm i \, \text{Wacame}\) is used for the expansion of function ArcCosc and its numerical implementation.
Exact values
The constants Wakame and Fune are exact; they can be evaluated with so many decimal digits as necessary. The approximations with 15 decimal digits are used in the numerical implementation of the related functions.
Some astronomers believe that the equatorial coordinates are related to the galactic coordinates through some approximations, and even think that \(\pi\) is approximate number. Such astronomers are cordially invited to write out their view on the classification of exact and approximate constants.
Etymology and terminology
The reason for using of the names instead of letters is the exhausting of the Latin and Greek alphabets and the name conflicts, when different constants from different areas of science happen to be used in the same investigation and, even worse, in the same computational code. The names from the movies Sazae-san seem to have no other special meaning is physics nor in mathematics, for this reasons they are considered as source of names.
The name of the constant is after name of the girl Wakame-chan in the serial Sazae-san. Wakame is good name for the global constant (which is used in many algorithms and articles), because Wakame–chan also remains "constant": during the end of century 20 and beginning of century 21, Wakame-chan and does not seem to learn anything new, she remains the same anecdotic person with a child mentality. The same refers to Sazae-san and other her relatives and friends; so, their names are also good to denote the mathematical constants.
Perhaps, the name Sazae-san functions can be used for the inverse functions of functions expressed as \(f(z)=\text{trigonometric}(z)/z\), where trigonometric means some of basic elementary functions considered in the school courses of mathematics.
Application
Constants Wakame and Fune are used in the expansion of function ArcCohc; at the branch point. This expansion is used in the numerical implementation of functions ArcCohc and ArcCosc in the complex plane. These functions are required for the calculation of modes of atomic waves guided between absorbing walls.
For the circular waveguides, similar functions should be constructed for BesslelJ and other cylinfric functions; in analogy with the Sazae-san functions and Sazae-san constants, those for the Bessel could be called Homer-Simpson functions and, correspondently, Homer-Simpson constants. The circular case is reported to be a little bit more difficult; for the function ArcBesseL, no efficient implementation is available.
Keywords
sinh,cosh, cohc, ArcCohc, ArcCosc, Sazae, Tarao, Fune, Sazae-san