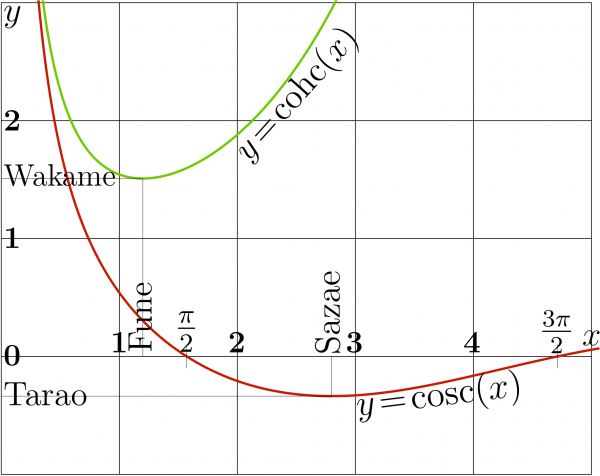
Sazae-san constants
The set of Sazae-san constants combines four constants, related to extrema and singularities of functions cosc and coshc and their inverse functions:
- \( \mathrm{Fune} \approx 1.199678640257734\)
- \( \mathrm{Wakame} \approx 1.50887956153832\)
- \(\mathrm{Sazae} \approx ~ 2.798386045783887\)
- \(\mathrm{Tarao} \approx\! -0.33650841691839534\)
with the following properties:
- \( \mathrm{cohc}'(\mathrm{Fune}) =0\)
- \( \mathrm{cohc}(\mathrm{Fune}) =\mathrm{Wakame}\)
- \( \mathrm{acohc}(\mathrm{Wakame}) =\mathrm{Fune}\)
- \( \mathrm{cosc}'(\mathrm{Sazae}) =0\)
- \( \mathrm{cosc}(\mathrm{Sazae}) =\mathrm{Tarao}\)
- \( \mathrm{acosc}(\mathrm{Tarao}) =\mathrm{Sazae}\)
Knowledge of these constants simplifies evaluation of functions ArcCohc and ArcCosc, which are inverse functions of Cohc and Cosc defined with
- \( \displaystyle \mathrm{cohc}(z) = \frac{\cosh(z)}{z} ~,~\) \(~ ~ \displaystyle \mathrm{cosc}(z) = \frac{\cos(z)}{z}\)
In future, the similar constants for functions ArcSihc and ArcSinc are expected to be loaded to simplify evaluation of the inverses of functions sihc and sinc defined with
- \( \displaystyle \mathrm{sihc}(z) = \frac{\sinh(z)}{z} ~,~ \) \(~ ~ \displaystyle \mathrm{sinc}(z) = \frac{\sin(z)}{z} \)
Etymology
The attempts to find several similar single–letter names for the constants that determine the asymptotical behavior of functions ArcCosc and ArcCohc were net successful. At the applications, the names of these constants often conflicted with other names of constants and functions already described in publications. For these reason, the constants related to functions Cosc, Cohc, ArcCosc and ArcCohc are assigned beautiful names.
The serial about Sazae-san is used to generate these names, because the protagonists of that movie look as constants, during a half-century, the mentality of Sazae-san, her brother, sisters and son remain the same, they do not seem to learn anything.
Paying tribute to creators of Sazae-san, this name is used to specify the sub-set of elementary functions, their inverse functions and the related constants.
Extensons
The equations above, suggested for the definition of the Sazae-san constants, may have many (countable set) of positive solutions. For the descrittion of highest modes of waveguide with absorbing walls, the constants are bumbered, beginning with unity; so, if the subscript of the Sazae-san constant is omitted, and it not specified that the notation refers to the array of constants, the subscript is supposed to be unity.
Mathematica software allows to evaluate s dozen of the Sazae-san constants of each kind without any worries about precision. For highest constants, the large number of digits should be specified at the evaluation.
For the evaluation of the absorption of the highest guided modes, the zeros of the asymptotical representation of the corresponding Sazae-san functions can be used.