File:Filogbigmap100.png
Original file (2,870 × 2,851 pixels, file size: 847 KB, MIME type: image/png)
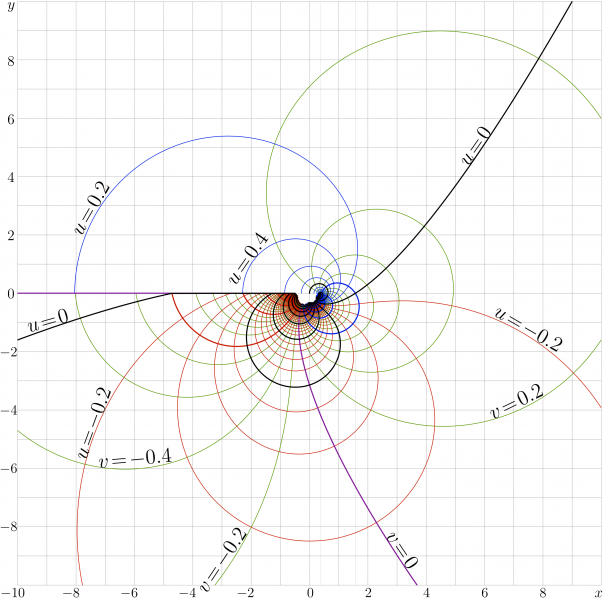
Complex map of function Filog.
Semantics of Filog
$\mathrm{Filog}(z)$ expresses the fixed point of logarithm to base $b\!=\!\exp(z)$.
Another fixed point to the same base can be expressed with
$\mathrm{Filog}(z^*)^*$
Algorithm of evaluation
Filog is expressed through the Tania function:
- $\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{Tania}\!\big(\ln(z)-1-\mathrm{i}\big)}{-z}$
Representation of the function
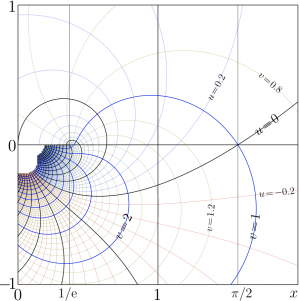
$f=\mathrm{Filog}(x+\mathrm{i} y)$ is shown in the $x,y$ plane with
levels $u=\Re(f)=\mathrm{cont}$ and
levels $v=\Im(f)=\mathrm{cont}$; thick lines correspond to the integer values.
The additional thin gridlines $x\!=\!\exp(-1)$ and $x\!=\!\pi/2$ are drawn. The first of them goes through the branchpoint $z=1/\mathrm e$, which is the branch point; the second goes through the point $z=\pi/2$, where the fixed points are $\pm \mathrm i$.
Properties of the function
$\mathrm{Filog}(z)$ has two singularities at $z\!=\!0$ and at $z\!=\!\exp(-1)$; the cutline is directed to the negative part of the real axis.
Except the cutline, the function is holomorphic. At the real values of the argument $0\!<\!z\!<\!\exp(-1)$, both at the upper side of the cut and at the lower side of the cut, the function has real values; in particular, at $z=\ln\big(\sqrt{2}\big)$, there values are integer [1]:
- $\mathrm{Filog}(z+\mathrm i o)=2$
- $\mathrm{Filog}(z-\mathrm i o)=4$
Approaching the branchpoint, the jump at the cut vanishes:
- $ \displaystyle \lim_{x\rightarrow 1/\mathrm e} \mathrm{Filog}(x+\mathrm i o)= \lim_{x\rightarrow 1/\mathrm e} \mathrm{Filog}(x-\mathrm i o)= \mathrm e$
Generator of curves
// Files ado.cin, conto.cin and filog.cin should be loaded to the working directory for the compilation of the C++ code below:
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
#include "filog.cin"
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
int M=400,M1=M+1;
int N=401,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("filogbig.eps","w");ado(o,2004,2004);
fprintf(o,"1002 1002 translate\n 100 100 scale\n");
DO(m,M1) X[m]=-10.+.05*(m-.2);
DO(n,200)Y[n]=-10.+.05*n;
Y[200]=-.0001;
Y[201]= .0001;
for(n=202;n<N1;n++) Y[n]=-10.+.05*(n-1.);
for(m=-10;m<11;m++){M(m,-10)L(m,10)}
for(n=-10;n<11;n++){M( -10,n)L(10,n)}
fprintf(o,".005 W 0 0 0 RGB S\n");
M(exp(-1.),-1)
L(exp(-1.), 1)
M(M_PI/2.,-1)
L(M_PI/2., 1)
fprintf(o,".003 W 0 0 0 RGB S\n");
DO(m,M1)DO(n,N1){g[m*N1+n]=9999; f[m*N1+n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y);
// c=Tania(z_type(-1.,-M_PI)+log(z))/(-z);
c=Filog(z);
p=Re(c);q=Im(c);
if(p>-15. && p<15. && q>-15. && q<15. ){ g[m*N1+n]=p;f[m*N1+n]=q;}
}}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=3.;q=1;
for(m=-10;m<10;m++)for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N,(m+.1*n),-q, q); fprintf(o,".001 W 0 .6 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N,-(m+.1*n),-q, q); fprintf(o,".001 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (m+.1*n),-q, q); fprintf(o,".001 W 0 0 .9 RGB S\n");
for(m=1;m<14;m++) conto(o,f,w,v,X,Y,M,N, (0.-m),-p,p); fprintf(o,".004 W .9 0 0 RGB S\n");
for(m=1;m<14;m++) conto(o,f,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".004 W 0 0 .9 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".004 W .6 0 .6 RGB S\n");
for(m=-11;m<14;m++) conto(o,g,w,v,X,Y,M,N, (0.+m),-p,p); fprintf(o,".004 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf filogbig.eps");
system( "open filogbig.pdf"); //for mac
// getchar(); system("killall Preview"); // for mac
// Copyleft 2012 by Dmitrii Kouznetsov
}
Generator of labels
For the compilation of the Latex source below, the curves of the complex map should be already generated and stored in file fIlog.pdf with the C++ code above.
<nomathjax>
\documentclass[12pt]{article} %<br>
\usepackage{geometry} %<br>
\paperwidth 2074pt %<br>
\paperheight 2060pt %<br>
\topmargin -96pt %<br>
\oddsidemargin -80pt %<br>
\textwidth 2090pt %<br>
\textheight 2066pt %<br>
\usepackage{graphicx} %<br>
\usepackage{rotating} %<br>
\newcommand \rot {\begin{rotate}} %<br>
\newcommand \ero {\end{rotate}} %<br>
\newcommand \rme {\mathrm{e}} %<br>
\newcommand \sx {\scalebox} %<br>
\begin{document} %<br>
\begin{picture}(2018,2040) %<br>
\put(50,40){\includegraphics{filogbig}} %<br>
\put(16,2024){\sx{4.3}{$y$}} %<br>
\put(16,1828){\sx{4.2}{$8$}} %<br>
\put(16,1628){\sx{4.2}{$6$}} %<br>
\put(16,1428){\sx{4.2}{$4$}} %<br>
\put(16,1228){\sx{4.2}{$2$}} %<br>
\put(16,1028){\sx{4.2}{$0$}} %<br>
\put(-11,828){\sx{4}{$-2$}} %<br>
\put(-11,628){\sx{4}{$-4$}} %<br>
\put(-11,428){\sx{4}{$-6$}} %<br>
\put(-11,228){\sx{4}{$-8$}} %<br>
\put(-8,0){\sx{4}{$-10$}} %<br>
\put(204,0){\sx{4}{$-8$}} %<br>
\put(404,0){\sx{4}{$-6$}} %<br>
\put(604,0){\sx{4}{$-4$}} %<br>
\put(804,0){\sx{4}{$-2$}} %<br>
\put(1046,0){\sx{4}{$0$}} %<br>
\put(1246,0){\sx{4}{$2$}} %<br>
\put(1446,0){\sx{4}{$4$}} %<br>
\put(1646,0){\sx{4}{$6$}} %<br>
\put(1846,0){\sx{4}{$8$}} %<br>
\put(2036,0){\sx{4.2}{$x$}} %<br>
%\put(40, 2){\sx{.8}{$1/\rme$}} %<br>
%\put(108, 0){\sx{1}{$1$}} %<br>
%\put(164, 2){\sx{.8}{$\pi/2$}} %<br>
\put(1600,1480){\sx{6}{\rot{55}$u\!=\!0$ \ero} } %<br>
\put(270,1240){\sx{6}{\rot{60}$u\!=\!0.2$ \ero} } %<br>
\put(800,1070){\sx{6}{\rot{55}$u\!=\!0.4$ \ero} } %<br>
\put(90,910){\sx{6}{\rot{16}$u\!=\!0$ \ero} } %<br>
\put(286,470){\sx{6}{\rot{70}$u\!=\!-0.2$ \ero} } %<br>
\put(1686,970){\sx{6}{\rot{-30}$u\!=\!-0.2$ \ero} } %<br>
\put(1686,610){\sx{6}{\rot{26}$v\!=\!0.2$ \ero} } %<br>
\put(1316,210){\sx{6}{\rot{-56}$v\!=\!0$ \ero} } %<br>
\put( 330,444){\sx{6}{\rot{5}$v\!=\!-0.4$ \ero} } %<br>
\put( 700,10){\sx{6}{\rot{56}$v\!=\!-0.2$ \ero} } %<br>
\end{picture} %<br>
\end{document} %<br>
%Copyleft 2012 by Dmitrii Kouznetsov
<nomathjax>
The resulting PDF file is converted to PNG with 100 pixels/inch resolution.
Rwfwewnces
- ↑ http://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.
Keywords
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 |  | 2,870 × 2,851 (847 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following 2 pages use this file: