Discrete Fourier

For natural number $N>1$, the Discrete Fourier is operator $\hat ふ_N$ acting on $N$-vector $A$ in such a way that

$\!\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \displaystyle (\hat ふ_{N} A)_n = \sum_{m=0}^{N-1} ふ_{n,m} A_m$

While deal with Fourier operators, it is convenient to begin numeration with zero. Elements of matrix $ふ$ are

$\!\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \displaystyle ふ_{m,n}=\frac{1}{\sqrt{N}} \exp\! \left( \frac{- \mathrm i ~2 ~\pi}{N}~m~n\right)$

The Fourier matrix $ふ$ is symmetric and unitary;

$\!\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ \displaystyle ふ_{m,n}= ふ_{n,m}$

$\!\!\!\!\!\!\!\!\!\!\! (4) ~ ~ ~ \displaystyle {\hat ふ}^*=　{\hat ふ}^{-1}$

in such a way, if $A=\hat ふ B$, then $B={\hat ふ}^* A$; so, ${\hat ふ}^\dagger={\hat ふ}^*$.

Different notations

Sometimes, the operator that deviate from $\hat ふ$ with factor $\sqrt{N}$ is considered; for such modified operator, the equation (4) does not hold, but the mofified operator is still called "Discrete Fourier" . Often, such an operator is denoted with latin letter $F$. (Sometimes the special font is used to avoid the confusion with parameters and functions.)

In order to avoid confusions, in TORI, the hiragana character ふ is used for the (normalized) Fourier operator, so, here, $ふ_N$ character denotes "DiscreteFourier with $N$ points" and nothing else.

Numeric implementation of the discrete Fourier

The numeric implementation of the Discrete Fourier is especially efficient when $N=2^k$ for some natural number $k$. For this case, the example of implementation is suggested below:

/* //Example of headers
#include<math.h> 
#include<stdio.h>
#include <stdlib.h>
#include <complex>
using namespace std;
#define z_type complex<double>
*/
// The "miminal" Fast Fourier Transform by Dmitrii Kouznetsov
// n should be 2^m for entire m ; o should be 1 or -1 ;

void fft(z_type *a, int N, int o) // Arry is FIRST!
{z_type u,w,t;  int i,j,k,l,e=1,L,p,q,m;
q=N/2;  p=2; for(m=1;p<N;m++) p*=2; 
p=N-1;  z_type y=z_type(0.,M_PI*o); j=0;
for(i=0;i<p;i++){ if(i<j) { t=a[j]; a[j]=a[i]; a[i]=t;}
                   k=q; while(k<=j){ j-=k; k/=2;} 
                   j+=k; }
for(l=0;l<m;l++)
{ L=e; e*=2; u=1.; w=exp(y/((double)L));
  for(j=0;j<L;j++)
  {  for(i=j;i<N;i+=e){k=i+L; t=a[k]*u; a[k]=a[i]-t; a[i]+=t;}
     u*=w;
} }
}

Approximation of the Fourier operator

Numerical approximation of the Fourier transform of function $~f(x)=\exp(−x^2/2)x^2(−3\!+\!x^2)~$ with $N\!=\!16$

For the continuous square-integrable functions, the discrete approximation with N points can be written with uniform mesh at pointd $x_n$, $n=0..N$, such that

$\displaystyle x_N=(n-N/2) \sqrt{\frac {2\pi}{N}}$

Let $f_n=f(x_n)$ then at the points $x_n$, the Fourier-transform $g=\mathcal F f$ can be approximated with the sum:

$ \displaystyle g(x_n)= \frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} \exp(\mathrm i x_n y) f(y) \mathrm d y

\approx g_n= \frac{1}{\sqrt{N}} \sum_{n=0}^{N-1} \exp(\mathrm i x_n x_m) f_m $

Then, at large $N\gg 1$, the array $g_n$ approximates $g(x_n)$. Using the routine fft for the discrete Fourier above, the numerical implementation of Fourier operator with the formula above may have the following form:

void fafo(z_type *b,int N,int o)
{ int j; z_type c; double q=sqrt(1./N);
for(j=0;j<N/2;j++) {c=b[j];b[j]=b[j+N/2];b[j+N/2]=c;}
fft(b,N,o);
for(j=0;j<N/2;j++) {c=b[j];b[j]=b[j+N/2]*q;b[j+N/2]=c*q;}
}

where $b$ is array to store the function and its Fourier, $N$ is number of points, and $o=1$ for the direct Fouried and $o=-1$ for the conjugated (inverse) Fourier.

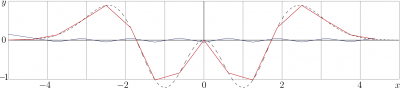
As an example, the figure at right shows discrete approximation of the self-Fourier function $~f(x)=\exp(−x^2/2)x^2(−3\!+\!x^2)~$ at the mesh with $N\!=\!16$. Values $f(x_n)$ and $g(x_n)$ almost coincide; they are shown with the segmented line. The difference scaled with factor $100$ is shown with the saw-like line that oscillates in vicinity of zero.

Approximation of the Fourier-series

Consider, for continuous function $f$ and given $N$, array

$F_n=f\left(\frac{2 \pi}{N} n\right)$

Then, at large $N$ the interpolation of array $F$ can be considered as approximation of function $f$, and its Discrete Fourier gives an approximation of the Fourier coefficients

$\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \displaystyle g_n=\frac{1}{2 \pi} \int_0^{2\pi} \exp\left( \mathrm i n x\right) f(x) \mathrm d x

\approx \displaystyle \frac{1}{2 \pi} \sum_{m=0}^{N-1} \exp\left(- \mathrm i n \frac{2 \pi}{N} m \right) \frac{2 \pi}{N}= \frac{1}{N} \sum_{m=0}^{N-1} \exp\left(\frac{2 \pi \mathrm i}{N} mn \right) = \frac{1}{\sqrt{N}} (\hat ふ_N F)_n $ in the Fourier series

$ \!\!\!\!\!\!\!\!\!\!\!\!\!\displaystyle

f(x)= \sum_{n=0}^{\infty} ~ g_n \exp( i n x) $

In such a way, the discrete Fourier operator can be used for approximation of both, the Fourier transform and the coefficients of the Fourier series. Similar approach can be used for other integral transforms; in particular, for the CosFourier and the SinFourier operators.