File:Kneserplot.png

Original file (1,798 × 1,347 pixels, file size: 185 KB, MIME type: image/png)
Explicit plot of the Keneser function (red curve),
\( \varphi=\mathrm{Kneeler}=\exp^{1/2} \)
The Keneser function \( \varphi \) is solution of equation
\( \varphi(\varphi(z)) = \exp(z) \)
Description
The Kneser function is implemented through the natural tetration tet and the arctetration ate:
\( \varphi(z)=\mathrm{tet}(1/2+\mathrm{ate}(z)) \)
Few additional lines are drown:
The short segment along line \( x\!=\!\mathrm{tet}(-1.5) \) and
Horisontal asymptotic \( y\!=\!\mathrm{tet}(-1.5) \)
Bisection of the First quadrant \( y\!=\!x \)
Exponential \( y\!=\!\exp(x) \)
C++ generator of map
// files ado.cin, conto.cin, fsexp.cin, fslog.cin should be loaded
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include<complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "ado.cin"
#include "fsexp.cin"
#include "fslog.cin"
#define M(x,y) fprintf(o,"%8.4f %8.4f M\n",x+0.,y+0.);
#define L(x,y) fprintf(o,"%8.4f %8.4f L\n",x+0.,y+0.);
int main(){ int j,k,m,n; DB x,y; z_type c,z;
FILE *o; o=fopen("kneserplo.eps","w"); ado(o,1220,920);
fprintf(o,"810 110 translate\n 100 100 scale\n");
for(m=-8;m<5;m++) {M(m,-1)L(m,8)}
for(n=-1;n<9;n++) {M( -8,n)L(4,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
M(-1,-1)L(4,4)
fprintf(o,"0 setlinecap 0 0 0 RGB .02 W S\n");
for(m=0;m<121;m++){ x=.1*(m-80); y=exp(x); if(m==0) M(x,y) else L(x,y) if(y>8.) break;};
fprintf(o,"0 setlinecap 0 0 1 RGB .08 W S\n");
for(m=0;m<121;m++){ x=.1*(m-80); z=x; c=FSLOG(z); c=FSEXP(.5+c); y=Re(c);
if(m==0) M(x,y) else L(x,y) if(y>8.) break;}
fprintf(o,"2 setlinecap 1 setlinejoin 1 0 0 RGB .08 W S\n");
z=-1.5; y=Re(FSEXP(z));
printf("y= %9.6lf\n",y);
M(-8,y)L(0,y)
M(y,y)L(y,0)
fprintf(o,"0 setlinecap 0 0 0 RGB .007 W S\n");
fprintf(o,"showpage\n");
fprintf(o,"%cTrailer\n",'%');
fclose(o);
system("epstopdf kneserplo.eps");
system( "open kneserplo.pdf"); //for macintosh
getchar(); system("killall Preview"); // For macintosh
}
Latex generator of curves
% File kneserplo.pdf should be generated with the cone above
\documentclass[12pt]{article}
\usepackage{geometry}
\paperwidth 1300pt
\paperheight 974pt
\textheight 1800pt
\textwidth 1800pt
\topmargin -88pt
\oddsidemargin -72pt
\usepackage{graphics}
\newcommand \sx {\scalebox}
\newcommand \ing {\includegraphics}
\usepackage{rotating}
\newcommand \rot {\begin{turn}}
\newcommand \ero {\end{turn}}
\pagestyle{empty}
\parindent 0pt
\begin{document}
\huge
\begin{picture}(1020,920)
\put(80,20){\ing{kneserplo}}
\put(40,906){\sx{3}{$y$}}
\put(40,710){\sx{3}{$6$}}
\put(40,510){\sx{3}{$4$}}
\put(40,310){\sx{3}{$2$}}
\put(40,110){\sx{3}{$0$}}
\put(24,-28){\sx{3}{$-8$}}
\put(224,-28){\sx{3}{$-6$}}
\put(424,-28){\sx{3}{$-4$}}
\put(624,-28){\sx{3}{$-2$}}
\put(880,-28){\sx{3}{$0$}}
\put(1080,-28){\sx{3}{$2$}}
\put(1260,-26){\sx{3.2}{$x$}}
\put(960,550){\rot{81}\sx{3.1}{$y\!=\!\exp(x)$}\ero}
\put(1086,418){\rot{69}\sx{3.1}{$y\!=\!\mathrm{Kneser}(x)$}\ero}
\put(1150,356){\rot{45}\sx{3.1}{$y\!=\!x$}\ero}
\put(894,50){\rot{0}\sx{3}{$y\!=\!\mathrm{tet}(-1.5)$}\ero}
\end{picture}
\end{document}
References
http://www.digizeitschriften.de/dms/img/?PID=GDZPPN002175851&physid=phys63#navi Hellmuth Kneser. Reelle analytische Lösungen der Gleichung \( \varphi(\varphi(x))=\mathrm e^x \) und verwandter Funktionalgleichungen. Journal für die reine und angewandte Mathematik / Zeitschriftenband (1950) / Artikel / 56 - 67
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane. Mathematics of Computation, 78: 1647-1670. DOI:10.1090/S0025-5718-09-02188-7
http://www.ils.uec.ac.jp/~dima/PAPERS/2010vladie.pdf D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45
http://www.ils.uec.ac.jp/~dima/PAPERS/2009supefae.pdf D.Kouznetsov, H.Trappmann. Superfunctions and sqrt of Factorial. (2010)
http://journal.kkms.org/index.php/kjm/article/view/428 William Paulsen. Finding the natural solution to f(f(x))=exp(x). Korean J. Math. Vol 24, No 1 (2016) pp.81-106.
https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen, Samuel Cowgill. Solving F(z + 1) = b ^ F(z) in the complex plane. Advances in Computational Mathematics, December 2017, Volume 43, Issue 6, pp 1261–1282
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 07:40, 1 January 2020 | 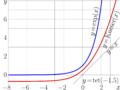 | 1,798 × 1,347 (185 KB) | T (talk | contribs) |
You cannot overwrite this file.
File usage
The following page uses this file: