Iterate of exponential

Iteration of exponent of real argument; $y=\exp^n(x)$ versus $x$ for various $n$

$u\!+\!\mathrm i v=\exp^1(x\!+\!\mathrm i y)=\exp(x\!+\!\mathrm i y)$

$u+\mathrm i v=\exp^{0.9}(x+\mathrm i y)$

$u+\mathrm i v=\exp^{0.5}(x+\mathrm i y)$

Iteration of exponential (or Iteration of rxponent) is function $f(z)=\exp^n(z)$, where upper superscript indicates the number of iteration.

This article is under construction. Wait for few days before to use it. 01:37, 27 July 2013 (JST)

The most often are the first iteration of exponent, $n=1$; $\exp^1=\exp$

and the minus first iteration, $n=-1$; $\exp^{-1} = \ln$.

Less often they appear with $n\ne \pm 2$; $\exp^2(z)=\exp(\exp(z))$, and $\exp^{-2}(z)=\ln(\ln(z))$. Other values of number of iteration are not usual.

Until 2008, there was no regular way to evaluate iteration of exponential for any non–integer number $n$ of iteration. However, with tetration tet, that is superfunction of exponent, and Arctetration ate, that is Abel function of exponent, the $n$th iteration can be expressed as follows:

$\exp^n(z)=\mathrm{tet}(n+\mathrm{ate}(z))$

This representation defines the $n$th iterate for any complex number $n$ of iterations.

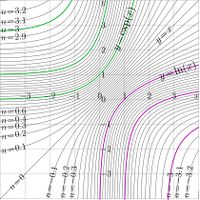
Complex maps of the $n$th iteration of exponential is shown in figures at right with lines $u=\Re(f(x+\mathrm i y))$ and lines $v=\Im(f(x+\mathrm i y))$ for various values $n$.

References

http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188.

http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf D. Kouznetsov. Solution of $F(x+1)=\exp(F(x))$ in complex $z$-plane. 78, (2009), 1647-1670

Keywords

Abel function, Arctetration, Exponent, Iteration, Superfunction, Tetration,,,,,,,