Korias
korias is asymptotic approximation of function kori. For $z\ne1$, funciton kori appears as
$\mathrm{kori}(z)=\displaystyle \frac{J_0\big( L_1 \sqrt{z} \big)}{1-z}$
where $L_1\approx 2.4$ is first zero of the Bessel function $J_0$. The corresponding limit for $z=1$ is assumed.
At large values of the argument, $|z|\gg 1$, the asymptotic approximation appears as korias defined with
$ \mathrm{korias}_m(x) = - \sqrt{\frac{2}{\pi L_1}} x^{-5/4} \, G_m(x)\, \cos\left( - \frac{\pi}{4} + L_1 \sqrt{x}\, F_m(x) \right) $
where
$G_m(x) = 1+\sum_{n=1}^{m} g_n x^{-n}$
$F_m(x) = 1+\sum_{n=1}^{m} f_n x^{-n}$
Coefficients $f$ and $g$ are estimated from the asymptotic expansion of function besselJ0. Approximations of these coefficients can be extracted from the generator of the map at the top.
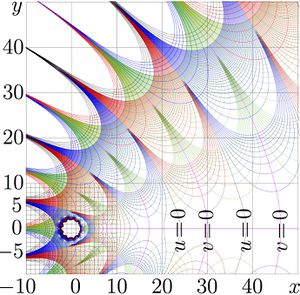
The map corresponds to $\,m\!=\!11\,$.
The approximation fails in vicinity of zero and at $|z|$ of order of unity.
The approximation is good for $|z|\gg 1$. In particular, for $\Re(z)>40$,
$|\mathrm{korias}(z) - \mathrm{kori}(z)| < 10^{-15}$
Approximation korias is designed for evaluation of integrand for the contour integral for function maga.
The approximation fails in vicinity of zero, for moderate values of the argument. This region appear as white spot in the complex map at the top for $m\!=\!11$. Outside the region with dense grid lines, the map of $\mathrm{korias})_{11}$ is visually the same, as the map for function kori. $m\!=\!11$ seems to provide the reasonable compromise between the order of approximation (which increases with the increase of $m$) and the range of validity, that reduces with increase of $m$; the larger is $m$, the larger is spot in the complex map, where the approximation is not valid.
References
Asymptotic expansion,
kori,
maga,
mori,
nori,
Morinaga function,
Pinhole waveguide