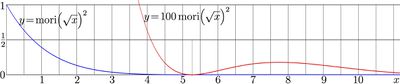
Nori
Identifier nori is used in TORI to denote holomorphic function, that in vicinity of the real axis \(\Re(z\ge 0\)) can be expressed through the morinaga function mori:
\(\mathrm{nori}(z)=\mathrm{mori}\big( \sqrt{z} \big) ^2=\,\) \(\displaystyle \frac{J_0\big(L \sqrt{z}\big)^2}{(1-z)^2}\)
where \(j_0=\,\)BesselJ0 is the zeroth bessel function, and \(L=\mathrm{BesselJZero}[0,1]\approx 2.404825557695773\) is its first zero.
The appropriate limit at \(z\!=\!1\) is assumed.
Properties
nori is entire holomorphic function. The cut of the function sqrt at negative values of the argument is compensated with symmetry of function mori, \(\mathrm{mori}(-z)=\mathrm{mori}(z)\), and the zero in the denominator is compensated by the corresponding zero of the Bessel function in the numerator.
Along real axis, in infinitely (exponentially) increases at large negative values of the argument, takes the integer value unity at zero, then decrease until its local minimum at its first zero at \((L_2/L_1)^2\), and then shows almost periodic oscillations with decaying amplitude and frequency. In order to show these oscillations, at the top picture, function nori is plotted, and also, it is plotted with scaling factor 100.
Complex map of function nori is shown at rites with levels \(u=\mathrm{const}\) and levels \(u=\mathrm{const}\),
\(u\!+\!\mathrm i v=\mathrm{nori} ( x\!+\!\mathrm i y) =\mathrm{mori}\big(\sqrt{x\!+\!\mathrm i y\,}\, \big)^2\)
in the \(x\),\(y\) plane.
Function nori remains positive and has countable set of zeros (of the second rank) along the positive part of the real axis,
\(\displaystyle \mathrm{nori}\left( \frac{L_n^2}{L_1^2}\right)=0\)
for integer \(n>1\), where \(L_n=\,\)BesselJZero\([0,n]\) is \(n\)th zero of the Bessel function of zero order.
Approximately, the first zeros are
\(~~ 5.268940431605221 ~\),
\( 12.949091948711433 ~\),
\( 24.042160379641810 ~\),
\( 38.548354669203904 ~\),
Expansion at zero
\(\displaystyle \mathrm{nori}(z)=1+\sum_{n=1}^\infty c_n\, z^n\)
\(c_1\approx -0.89159298147339226059\)
\(c_2\approx~~ 0.35230527599303366777\)
\(c_3\approx -0.082789885057149559847\)
\(c_4\approx~~ 0.013126814743581504735\)
\(c_5\approx -0.0015103376896127445983\)
\(c_6\approx~~ 0.00013234402135557275356\)
if evaluated with complex double variables, the first 24 terms of this expansion provide of order of 15 correct decimal digits for \(|z|<8\). In particular, it is more precise and faster, than the original representation through the mori function and the Bessel function; the last is especially poor in vicinity of unity, where no nominator in the definition becomes zero.
In vicinity of the \((L_2/L_1)^2\), where nori becomes zero, the expansion at this point is more precise.
Expansion at \((L_2/L_1)^2\)
As nori is entire function, it can be expanded to convergent Taylor series in any point. In particular, the expansion at its first zero appears as
\(\displaystyle \mathrm{nori}\left( \frac{L_2^2}{L_1^2}+z\right)=\sum_{n=2}^{\infty} c_n\, z^n\)
Approximations of the first coefficients are:
\(c_2= ~ 0.00174332257160181945072326757479\)
\(c_3=\! -0.00114761496984019073111080831864\)
\(c_4=~ 0.000340103481720677645944329914889 \)
\(c_5=\! - 0.0000609020923565221809007524371617\)
Approximations for 24 coefficients \(c\) can be extracted from the generator of the complex map above; this expansion is used to evaluate nori is that generator (and to plot the complex map). In the range to the figure, it allows to evaluate nori giving of order of 14 correct decimal digits. In particular, this representation covers both, \(z=0\) (origin of coordinates) and the next zero of function nori, id eest, \(z=\mathrm{noriz}_3=(L_3/L_1)^2\). Perhaps, numeration of zeros of function nori should begin with two, in order to simplify the relation with zeros of the Bessel function.
The polynomial is good function for the analytic integration with exponential; so, the representation with the truncated series above can be useful for the evaluation of the Fourier integrals with function nori.
Asymptotic at large argument
Asymptotic of nori at large values of its argument can be written as follows:
\(\mathrm{nori}(z) \approx\, \displaystyle \frac{1}{ 4\pi L z^{5/2}}\left(4+\left(8-\frac{1}{2L^2}\right)\frac{1}{z} +\, ..\,\right) \)\(\displaystyle +\, \frac{\sin\left(2 L \sqrt{z}\right)} { 4\pi L z^{5/2}} \left(4+\frac{8-\frac{5}{8 L^2}}{z}+\, .. \right) \) \(\displaystyle +\, \frac{\cos\left(2 L\sqrt{z}\right)}{4\pi L z^{3}} \left(-\frac{1}{L}+\left(\frac{21}{32 L^3}-\frac{2}{L}\right) \frac{1}{z} +\, ..\right) \)
or even simpler
\(\mathrm{nori}(z) \approx\, \displaystyle \frac{1+\sin\big( 2 L \sqrt{z}\,\big)}{ \pi L z^{5/2}} \left(1 + O(1/z)^{1/2} \right) \)
Approximation through kori
The range of approximation of the fit above can be extended using function
\(\mathrm{kori76fit}= \prod_{n=2}^7\! \left(1-\frac{L_1^2}{L_n^2}x\right)~ \frac{1+\sum_{n=1}^6 a_n x^n}{1+\sum_{n=1}^6 b_n x^n} \)
where \(L_n=\mathrm{BesselJZero}[0,n]\) and coefficients \(a\) and \(b\) are:
\(\begin{array}{l} a_1=-0.04844698269548584 \\ a_2= 0.0010028289633265202 \\ a_3= -0.000011428855401098336\\ a_4= 7.61813379974462\times 10^{-8}\\ a_5= -2.8376606186641804\!\times\! 10^{-10}~\\ a_6= 4.651275051439759\times 10^{-13} \end{array}\) \(\begin{array}{l} b_1= 0.03223483760044156\\ b_2= 0.0004974915308429358\\ b_3= 4.7768603073237505\times 10^{-6}\\ b_4= 3.071615607112112\times 10^{-8}\\ b_5= 1.292095753771865\times 10^{-10}\\ b_6= 2.925186494186955\times 10^{-13} \end{array} \)
Approximation is the following:
\(\displaystyle \mathrm{nori}(z) \approx \mathrm{korifit76}(z)^2\)
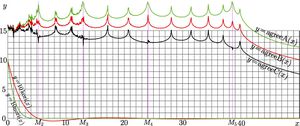
In order to indicate the precision and the range of validity of approximation korifit76, the figure at right shore the agreements
\(\mathrm{agreeA}(x)= - \lg\! \Big( \big|\mathrm{korifit76}(x)^2-\mathrm{nori}(x)\big|\Big)\)
\(\mathrm{agreeB}(x)= - \lg\! \Big( \big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big| \Big)\)
\(\displaystyle \mathrm{agreeC}(x)\!=\! - \lg \left(\!\frac {\big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big|}{\big|\mathrm{korifit76}(x)\big| \!+\! \big|\mathrm{kori}(x)\big|}\right)\)
Roughly, the agreements indicate, how many correct decimal digits can be achieved at the use of korifit76 instead of function kori. In particular the upper curve, \(y=\mathrm{agreeA}(x)\), shows, that at the integration with this approximation from zero to at least 42 with a complex exponent, the errors of fitting do not make the precision worse, as it is determined by the precision of evaluation of function in vicinity of zero (where it is of order of unity.
In the complex plane, the range of function nori is roughly, the ellipse, tat extends from \(-1\) to \(42\) by the along the real part, and from \(-2\) to \(2\) along the imaginary part. The purpose of this fit is approximation for the contour integral with exponential, that is a little bit slow if evaluated by the straightforward integration along the real axis. For the contour integral, it is important, that the integrated function is approximated in "one piece" with some holomorphic function; then deformation of the contour of integration do not affect the result.
Application
Nori function is used for evaluation of function maga, that, for the real argument, can be expressed as follows:
\(\mathrm{maga}(q)= \displaystyle 1-\left| \int_0^\infty \mathrm{nori}(q)\, \exp(\mathrm i\, q\, t)\, \mathrm d q\right|^{\,\,2}\)
Function maga expresses the loss of the principal Bessel mode in the idealised pinhole waveguide in the paraxial approximation.
For complex values of the argument, function maga can be defined with
\(\mathrm{maga}(q)= \displaystyle 1- \) \(\displaystyle \left(\int_0^\infty \mathrm{nori}(q)\, \cos(q\, t)\, \mathrm d q\right)^{2} \) \(\displaystyle -\, \left(\int_0^\infty \mathrm{nori}(q)\, \sin(q\, t)\, \mathrm d q\right)^{2}\)
Formally, the integrals above appear as CosFT and SinFT. However, the straightforward implementation shows poor performance, in particular, at the edge of the range of integration. This observation caused the need to perform certain analysis of functions mori, nori, naga and maga.
The precise evaluation of the integrals above happen to be non–trivial and may require deformation of the contour of integration in the complex plane. For this reason, the knowledge of the holomorphic properties of the integrand and its components are important; in particular the efficient implementations are necessary for all the functions involved.
References
Keywords
Bessel function, BesselJ0, BesselJZero, C++, Makoto Morinaga, Mathematica, Mori, Morinaga function, Nori, Pinhole waveguide Spacial function