Korifit76
korifit76 is rational aproximation of function kori\((x)=\displaystyle \frac{J_0(L_1 \sqrt{x})}{1\!-\!x}\) elaborated for the numerical implementation of integrals with function nori\((x)=\,\)kori\((x)^2\). Here, \(L_n=\mathrm{BesselJZero}[0,n]\); in particular, \(L_1=\,\)BesselJZero\((0,1)\approx 2.4\)
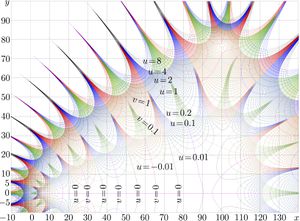
Complex map of function korifit76 is shown in the top figure with lines \(u\!+\!\mathrm i v=\mathrm{korifit76}(x\!+\!\mathrm i y)\). For comparison, below, complex map of the approximated function kori is shown in the same notations.
Definition
The approximation is defined with function
\(\mathrm{kori76fit}(x)=\displaystyle \prod_{n=2}^7\! \left(1-\frac{L_1^2}{L_n^2}x\right)~ \frac{1+\sum_{n=1}^6 a_n x^n}{1+\sum_{n=1}^6 b_n x^n} \)
where \(L_n=\mathrm{BesselJZero}[0,n]\) and coefficients \(a\) and \(b\) are:
\(\begin{array}{l} a_1=-0.04844698269548584 \\ a_2= 0.0010028289633265202 \\ a_3= -0.000011428855401098336\\ a_4= 7.61813379974462\times 10^{-8}\\ a_5= -2.8376606186641804\!\times\! 10^{-10}~\\ a_6= 4.651275051439759\times 10^{-13} \end{array}\) \(\begin{array}{l} b_1= 0.03223483760044156\\ b_2= 0.0004974915308429358\\ b_3= 4.7768603073237505\times 10^{-6}\\ b_4= 3.071615607112112\times 10^{-8}\\ b_5= 1.292095753771865\times 10^{-10}\\ b_6= 2.925186494186955\times 10^{-13} \end{array} \)
Approximation is the following:
\(\displaystyle \mathrm{nori}(z) \approx \mathrm{korifit76}(z)^2\)
This approximation is valid, roughly, for \(-1\!<\!\Re(x)\!<\! 40\) and \(|\Im(z)|<2\), providing several significant figures in this range.
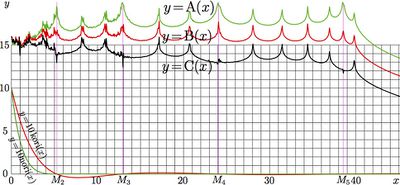
In order to indicate the precision and the range of validity of approximation korifit76 for real argument, the figure at right shows agreements
\(\mathrm{A}(x)= \) \(- \lg\! \Big( \big|\mathrm{korifit76}(x)^2-\mathrm{nori}(x)\big|\Big)\)
\(\mathrm{B}(x)= \) \(- \lg\! \Big( \big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big| \Big)\)
\(\displaystyle \mathrm{C}(x)\!=\!\) \(\displaystyle - \lg \left(\!\frac {\big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big|}{\big|\mathrm{korifit76}(x)\big| \!+\! \big|\mathrm{kori}(x)\big|}\right)\)
The additional vertical lines in the plot at right indicates zeros of function korifit76; they are defined with
\(M_n=(L_n/L_1)^2\) for \(n=2\, ..\, 5\); they coincide with zeros the approximated function.
At the bottom, the approximated function and its square are shown, scaled with factor 10, id est,
\(y=10\,\mathrm{kori}(x)\) and
\(y=10\,\mathrm{nori}(x)=10\,\mathrm{kori}(x)^2\),
Roughly, the agreements indicate, how many correct decimal digits can be achieved at the use of korifit76 instead of function kori. In particular, the upper curve, \(y=\mathrm{A}(x)\), shows, that at the integration with this approximation from zero to at least 42 with a complex exponent, the errors of fitting do not make the precision worse, as it is determined by the precision of evaluation of function in vicinity of zero (where it is of order of unity.
In the complex plane, the range of precise approximation by korifit76 is, roughly, the ellipse, that extends from \(-1\) to \(40\) by the along the real part, and from \(-2\) to \(2\) along the imaginary part.
Numerical implementation
The C++ implementation of the complex double version of Korifit76 is denoted korifit76.cin
Application
The purpose of this fit is approximation for the contour integral with exponential, that is a little bit slow if evaluated by the straightforward integration along the real axis. For the contour integral, it is important, that the integrated function is approximated in "one piece" with some holomorphic function; then deformation of the contour of integration do not affect the result.
If the integration begins with zero, where the approximated function is of order of unity, then, the error of this approximation does not affect the error of the result of computation with complex double variables (or just double for the integration along the real axis.
References