Cosc
Cosc\(=\)cosc is elementary function defined with
- \( \displaystyle \mathrm{cosc}(z)=\frac{\cos(z)}{z}\)
History and ethimology
First, the name Cip was suggested, as derivative of the IntegralCos, named also Ci, id est, "Ci-Prime"; and the name ArcCip of the inverse function had been suggested. Then it happened that the similar formalism should be applied for function sinc defined with
- \( \displaystyle \mathrm{sinc}(z) = \frac{ \sin(z)}{z}\)
For the zero argument, it is defined that \(\mathrm{sinc}(0)=1\). Function sinc already has etablishen name [1]. Therefore, the natural choice for the similar function with cos instead of sin is cosc, and the good name for the inverse function is ArcCosc or simplly acosc.
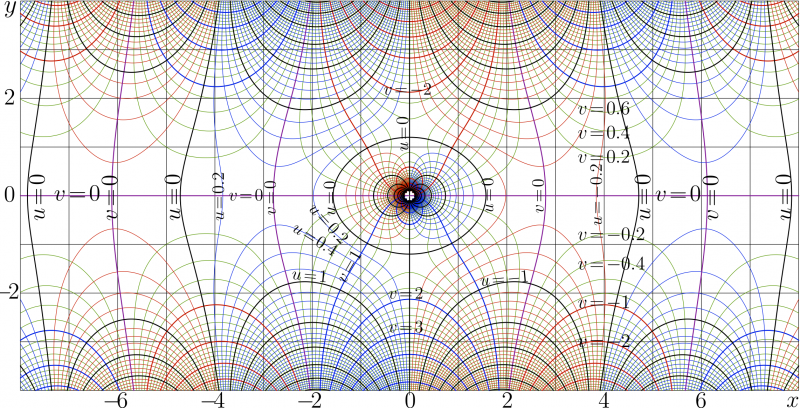
Complex map of cosc
The complex map of function cosc is shown at the upper figure. It represents \(f\!=\!\mathrm{cosc}(x\!+\!\mathrm i y)\) in the \(~x\), \(y~\) plane. Levels \(~u\!=\!\Re(f)\!=\!\mathrm{cost}~\) and levels \(~v\!=\!\Im(f)\!=\!\mathrm{cost}~\) are drawn.
Click the image to see the code used for its generation.
Symmetry
Cosc is real antisymmetric function:
- \(\mathrm{cosc}(-z)=- \mathrm{cosc}(z)\)
- \(\mathrm{cosc}(z^*)=-\mathrm{cosc}(z)^*\)
Related functions
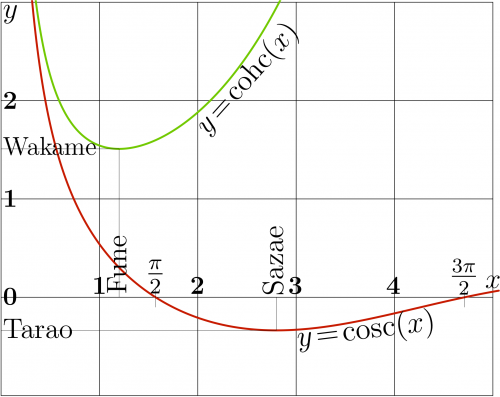
For the case of argument with small real part (but, perhaps, large imaginary part), the modified function cosh is useful;
- \(\displaystyle \mathrm{cohc}(z)=\frac{\cosh(z)}{z}= \mathrm i ~ \frac{\cos(\mathrm{i}\, z)}{\mathrm{i} \, z}= \mathrm i ~ \mathrm{cosc}(\mathrm i z)\)
In the part of the complex plane, the similar relation takes place for the inverse functions, id est, for ArcCosc and ArcCohc.
The analysis of cohc and its inverse function ArcCohc is used to make the efficient implementation of the inverse function ArcCosc=cosc\(^{-1}\).
Behavior along the real axis
Due to the symmetry above, it is sufficient to consider behavior of cosc along the positive part of the real axis. Graphic of cosc is comparef to that for cohc in the figure at right. Values between zero and Sazae are used in the construction of function ArcCosc.
The expansion at zero can be written as follows:
- \(\displaystyle \mathrm{cosc}(z) = \sum_{n=0}^{\infty} \frac{(-1)^n z^{2n-1}} {(2n)!} \) \(\displaystyle = \frac{1}{z} - \frac{z}{2} +\frac{z^3}{24}-\frac{z^5}{720}+...\)
The series converges in the whole complex plane except \(z\!=\!0\).
Function cosc decreases from \(+\infty\) at zero, takes value zero at \(\pi\) and continues decreasing until its minimum called Sazae;
- \( \mathrm{Sazae} \approx 2.798386045783887\)
- \( \mathrm{cosc}(\mathrm{Sazae})=\mathrm{Tarao} \approx −0.33650841691839534\)
- \( \mathrm{cosc}'(\mathrm{Sazae})=0\)
The expansion at Sazae has form
- \(\mathrm{cosc}(\mathrm{Sazae}+t)= \mathrm{Tarao} \) \( \displaystyle -\frac{ \mathrm{Tarao}}{2}t^2 -\frac{ \mathrm{Tarao}}{3 ~ \mathrm{Sazae}} t^3 \) \( \displaystyle + \frac{\left(\mathrm {Sazae}^2\!-\!8\right) \mathrm{Tarao}}{24 ~ \text{Sazae}^2} t^4 + .. \)
Mathematica allows to calculate many terms of this expansion. The radius of convergence of the series is \) \mathrm{Sazae} \approx 2.798386045783887\(, which is just distance to the closest singularity. At larger values of the argument, cosc oscillates, slowly decaying to zero. =='"`UNIQ--h-5--QINU`"'Invese function== In [[TORI]], there is special article about function [[ArcCosc]]=cosc\)^{-1}$. For the beginning of year 2012, the only principal branch of the inverse function is described and supplied with the efficient numerical implementation in C++. The other branches are expected be considered in the similar way.