BesselJ1
BesselJ1 or \(J_1\) is Bessel function of first order;
- \(\!\!\!\! \mathrm{BesselJ1}(z)=J_1(z)= \mathrm{BesselJ}[1,z]\)
Function \(f=\mathrm{BesselJ1}\) satisfies the Bessel equation [1]
- \( \!\!\!\! f''(z)+f'(z)/z + (z^2\!-\!1)f(z) = 0\)
with boundary conditions
- \(f(0) = 0~\) and \(~f'(0)=1/2\)
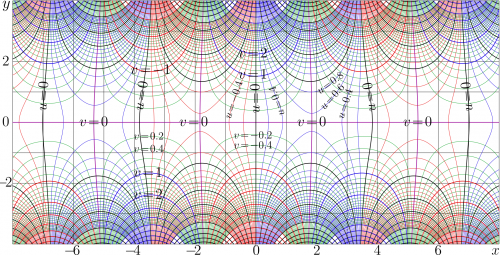
The complex map of \(f=J_1(x+\mathrm i y)\) is shown at right in the \(x,y\) plane with levels \(u=\Re(f)=\mathrm {const} ~\) and levels \(v=\Im(f)=\mathrm {const} ~\).
Relation to other Bessel functions
- \( J_0'(z)=-J_1(z)\)
- \(\displaystyle 1-J_0(z)=\int_0^z J_1(t)~\mathrm d t \)
Expansions
\(J_1\) is entire function, the series
- \(\displaystyle J_1(z) = \frac{z}{2} \sum_{n=0}^\infty \frac{(-z^2/4)^n}{(n\!+\!1)~ \mathrm{Factorial}(n)^2}\)
converges for any complex \(z\) and can be used to plot the complex map at least for \(z<10\) withe the complex(double) arithmetics is available. For large values of \(|z|\), the asymptotic expansion can be used for the precise evaluation:
- \(\displaystyle J_1(z)= \)
- \(\displaystyle \sqrt{\frac{2}{\pi z}} \cos\left(\frac{\pi}{4}+z\right) \left( -1 - \frac{15}{128 z^2} +\frac{4725}{32768 z^4} - \frac{2837835}{4194304 z^6} + \frac{14783093325}{ 2147483648 z^8} - \frac{33424574007825}{274877906944 z^{10}} +O\left(\frac{1}{z^{12}}\right) \right) +\)
- \(\displaystyle \sqrt{\frac{2}{\pi z}} \sin\left(\frac{\pi}{4}+z\right) \left( \frac{3}{8 z} - \frac{105}{1024 z^3} + \frac{72765}{262144 z^5} - \frac{66891825}{33554432 z^7} + \frac{468131288625}{17179869184 z^9} - \frac{1327867167401775}{2199023255552 z^{11}} +.. \right) \)
This asymptoric expansion is used for the numerical implenentation. However, \(z\) should not approach the negative part of the real axis. For the case \(\Re(z)<0\), the symmetry
- \(J_1(z)= - J_1(-z)\)
is used.
Mathematica allows to calculate a dozen of term of this expansion; they can be extracted also from the complex(double) implementation Besselj1.cin.
Evaluation at real argument
At real values of the argument, the GNU library [2] can be used for the evaluation.
The BesselJ1 is related to the BesselJ0 as follows:
- \( J_1(z)=-J_0'(z)\)
Keywords
BesselJ0, Bessel function, Special function, Entire function, Cylindric function
References
http://mathworld.wolfram.com/BesselFunctionoftheFirstKind.html