File:GCtudent12345big.png
Revision as of 09:23, 10 May 2024 by T (talk | contribs) (== Summary == {{oq|GCtudent12345big.png|}} <big><big> Cumulative function Ctudent for the Student Distribution: \( y= \mathrm{Ctudent}_n(x) \) versus \(x\) <poem> for \( n = 1 \) (pink), the sane as for the Cauchi Distribution \( n = 2...)
Size of this preview: 467 × 600 pixels. Other resolutions: 187 × 240 pixels | 1,653 × 2,122 pixels.
Original file (1,653 × 2,122 pixels, file size: 57 KB, MIME type: image/png)
Summary
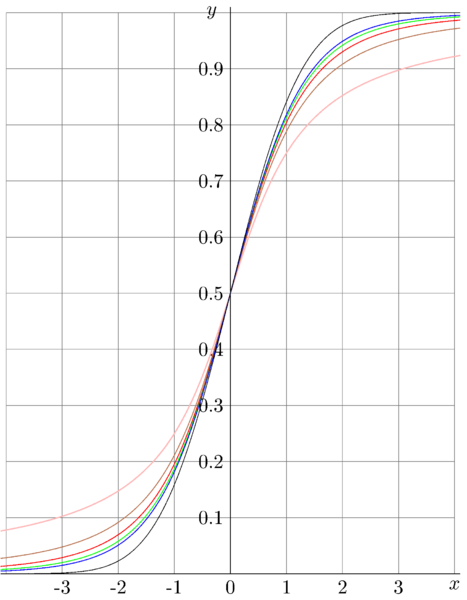
Cumulative function Ctudent for the Student Distribution:
\( y= \mathrm{Ctudent}_n(x) \) versus \(x\)
for
\( n = 1 \) (pink), the sane as for the Cauchi Distribution
\( n = 2 \) (brown)
\( n = 3 \) (red)
\( n = 4 \) (green)
\( n = 5 \) (blue)
\( n = \infty \) (black), the same as for the Normal Distribution
The explicit representations by Wikipedia are used
C++ generator
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
float Ctudent1(float x){ return .5 + M_1_PI * atan(x); }
float Ctudent2(float x){ return .5 + x/sqrt(8+4*x*x); }
float Ctudent3(float x){ float y=x/sqrt(3.); return .5 + M_1_PI*( y/(1+y*y) + atan(y) ); }
float Ctudent4(float x){ float y=x/sqrt(4.+x*x); return .5 + .75*y*(1.-y*y/3.); }
//float Ctudent5(float x){ float y=1./sqrt(5.+x*x); return .5 + M_1_PI * ( sqrt(5.)*x*y*(1.+(10./3.)*y) + atan(x/sqrt(5.)) ); }
float Ctudent5(float x){ return .5 + M_1_PI * ( x/sqrt(5.)/(1.+x*x/5.)*(1.+(2./3.)/(1+x*x/5.)) + atan(x/sqrt(5.)) ); }
//float Gau(float x){ return 1./sqrt(2*M_PI) * exp(-x*x/2); }
float Gerf(float x){ return .5*(1. + erf(M_SQRT1_2*x) ); }
int main()
{ int n; FILE *o; o=fopen("GCtudent12345big.tex","w");
fprintf(o,"\\documentclass{standalone}\n");
fprintf(o,"\\usepackage{tikz}\n");
fprintf(o,"\\usepackage{graphicx}\n");
fprintf(o,"\\begin{document}\n");
fprintf(o,"\\scalebox{7}{\\begin{tikzpicture}\n");
fprintf(o,"\\draw [help lines] (-4,0) grid (4,10);\n");
fprintf(o,"\\draw(-4.1,0) -- (4.1,0) ;\n");
fprintf(o,"\\draw(0,0) -- (0,10.1) ;\n");
for(n=-3;n<4;n++) fprintf(o,"\\draw (%d,0) node[below] {%d};\n",n,n);
fprintf(o,"\\draw (%d,0) node[below] {$x$};\n",n);
for(n=1;n<10;n++) fprintf(o,"\\draw (0,%d) node[left] {0.%d};\n",n,n);
fprintf(o,"\\draw (0,%d) node[left] {$y ~$};\n",n);
float x,y;
for(n=0;n<165;n++)
{ x=-4.1+.05*n; y=10*Ctudent1(x);
if(n==0) fprintf(o,"\\draw[line width=.6, pink] (%6.3f,%5.3f)",x,y);
else fprintf(o," -- (%6.3f,%5.3f)",x,y);
}
fprintf(o,";\n");
for(n=0;n<165;n++)
{ x=-4.1+.05*n; y=10*Ctudent2(x);
if(n==0) fprintf(o,"\\draw[line width=.4, brown] (%6.3f,%5.3f)",x,y);
else fprintf(o," -- (%6.3f,%5.3f)",x,y);
}
fprintf(o,";\n");
for(n=0;n<165;n++)
{ x=-4.1+.05*n; y=10*Ctudent3(x);
if(n==0) fprintf(o,"\\draw[line width=.4, red] (%6.3f,%5.3f)",x,y);
else fprintf(o," -- (%6.3f,%5.3f)",x,y);
}
fprintf(o,";\n");
for(n=0;n<165;n++)
{ x=-4.1+.05*n; y=10*Ctudent4(x);
if(n==0) fprintf(o,"\\draw[line width=.4, green] (%6.3f,%5.3f)",x,y);
else fprintf(o," -- (%6.3f,%5.3f)",x,y);
}
fprintf(o,";\n");
for(n=0;n<165;n++)
{ x=-4.1+.05*n; y=10*Ctudent5(x);
if(n==0) fprintf(o,"\\draw[line width=.4, blue] (%6.3f,%5.3f)",x,y);
else fprintf(o," -- (%6.3f,%5.3f)",x,y);
}
fprintf(o,";\n");
for(n=0;n<165;n++)
{ x=-4.1+.05*n; y=10*Gerf(x);
if(n==0) fprintf(o,"\\draw[line width=.3, black] (%6.3f,%5.3f)",x,y);
else fprintf(o," -- (%6.3f,%5.3f)",x,y);
}
fprintf(o,";\n");
fprintf(o,"\\end{tikzpicture}}\n");
fprintf(o,"\\end{document}\n");
fclose(o);
system("pdflatex GCtudent12345big.tex");
system("open GCtudent12345big.pdf");
system("convert GCtudent12345big.pdf png8:GCtudent12345big.png");
system("identify GCtudent12345big.png");
}
References
Keywords
«Cauchi Distribution», «Ctudent», «Gauss», «Normal Distribution», «Student», «Student Distribution»,
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 09:23, 10 May 2024 |  | 1,653 × 2,122 (57 KB) | T (talk | contribs) | == Summary == {{oq|GCtudent12345big.png|}} <big><big> Cumulative function Ctudent for the Student Distribution: \( y= \mathrm{Ctudent}_n(x) \) versus \(x\) <poem> for \( n = 1 \) (pink), the sane as for the Cauchi Distribution \( n = 2... |
You cannot overwrite this file.
File usage
The following page uses this file: