File:TetSheldonImaT.png

File
File history
File usage
Metadata

Size of this preview: 800 × 180 pixels. Other resolutions: 320 × 72 pixels | 4,359 × 980 pixels.

Original file ‎(4,359 × 980 pixels, file size: 598 KB, MIME type: image/png)

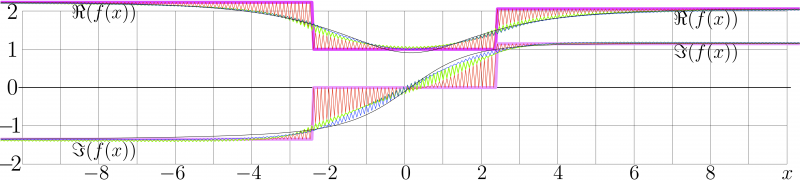
Few iterations at the Iterated Cauchi for the Tetration to Sheldon base.

The holomorphic solution $F$ of equation

$ \!\!\!\!\!\!\!\! (1) ~ ~ ~

\exp(a F(z))=F(z\!+\! 1)$ is considered for

$\!\!\!\!\!\! (2) ~ ~ ~

a=\ln(s) = \ln( 1.52598338517+0.0178411853321 i) \approx 0.4227073870410604+0.0116910660021443 i $ where $s$ is the Sheldon number.

The solution $F$ is supposed to have the specific boundary behavior:

$\!\!\!\!\!\! (3) ~ ~ ~

F(x+ i \infty) = Z_{\mathrm o}=\mathrm{Filog}(a)$

$\!\!\!\!\!\! (4) ~ ~ ~

F(x- i \infty) = Z_{\mathrm c}=\mathrm{Filog}(a^*)^*$ where Filog is fixed point of the logarithm.

Approximation

The solution is approximated first along the imaginary axis,

$\!\!\!\!\!\! (5) ~ ~ ~ F(iy)=f(x)$

where $f$ is solution of equation

$\!\!\!\!\!\! (5) ~ ~ ~ \displaystyle

f(x) = K(ix) + \frac{1}{2\pi} \int_{-A}^{A} \frac{ \exp(a f(y) ) }{ 1+ \mathrm i y- \mathrm i x} \mathrm d y + \frac{1}{2\pi} \int_{-A}^{A} \frac{ \log(f(y))/a }{-1+\mathrm i y- \mathrm i x} \mathrm d y $ with

$\!\!\!\!\!\! (6) ~ ~ ~ \displaystyle

K(z)= Z_{\mathrm o} \left(\frac 12-\frac{1}{2\pi\mathrm i} \ln \frac {1-\mathrm i A +z} {1+\mathrm i A-z} \right) + \displaystyle Z_{\mathrm c} \left( \frac 12-\frac{1}{2\pi\mathrm i} \ln \frac {1-\mathrm i A -z} {1+\mathrm i A+z} \right) $

where $A$ is large positive constant.

The Gauss-Legendre quadrature formula ^[1] is used for the numerical implementation of the integration with number of nodes 2048. The update by (5) is realized node by node; first even nodes from left to right; then odd ones from right to left. The details can be revealed from the algorithm below.

Generators of the figure

The follpwing files should be loaded to the working directory for the compilation of the generator below: ado.cin (header for graphics)
filog.cin (evaluation of Filog)
GLxw2048.inc (nodes and weights of the Gauss-Kegendre quadrature formula

C++ generator of curves

#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) (x).real()
#define Im(x) (x).imag()
#define I z_type(0.,1.)
#define DO(x,y) for(x=0;x<y;x++)
#include "ado.cin"
#include "filog.cin"
#define M(x,y) fprintf(o,"%5.3f %5.3f M\n",1.*(x),1.*(y));
#define L(x,y) fprintf(o,"%5.3f %5.3f L\n",1.*(x),1.*(y));
#define o(x,y) fprintf(o,"%5.3f %5.3f o\n",1.*(x),1.*(y));
main(){ int J,j,k,m,n; DB x,y, u, t; z_type z,c,d, cu,cd; 
#include "GLxw2048.inc"
z_type b=z_type( 1.5259833851700000, 0.0178411853321000);
z_type a=log(b);
z_type Zo=Filog(a);
z_type Zc=conj(Filog(conj(a)));
int K=NPO; DB A=32.; printf("K=%3d A=%3.1f\n",K,A);
z_type E[K],F[K],G[K],H[K];
FILE *o;o=fopen("TetSheldonIma.eps","w");ado(o,2200,450);
fprintf(o,"1100 201 translate\n 100 100 scale\n");
for(j=-10;j<11;j+=1){M(j,-2)L(j,2);}
M(-10 , 2)L(10 , 2); 
M(-10 , 1)L(10 , 1); 
M(-10 ,-1)L(10 ,-1);
M(-10 ,-2)L(10 ,-2);
  fprintf(o,".006 W S\n");
M(-10.1,0)L(10.1,0);  fprintf(o,".02 W S\n");
fprintf(o,".01 W S\n 1 setlinejoin 1\n");
DO(n,K){y=GLx[n]*A; 
	if(y<-2.4)  	E[n]=F[n]=G[n]=Zc;
	else {if(y>2.4)	E[n]=F[n]=G[n]=Zo;
		else {  F[n]=c=1. ;//f3(z_type(0.,y));
			E[n]=log(c)/a;
			G[n]=exp(a*c);	
		     }
	     }
	}
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Re(F[k]);if(j==0)M(y,u)else L(y,u)}
fprintf(o,".08 W 1 .2 1 RGB S\n");
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Im(F[k]);if(j==0)M(y,u)else L(y,u)}
fprintf(o,".08 W 1 .6 1 RGB S\n");
for(n=0;n<K;n+=2)
{ y=GLx[n]*A; z=z_type(0.,y); c=0.;  //printf(" %3d",n);
  DO(k,K){t=A*GLx[k]; c+= GLw[k]*( G[k]/(z_type( 1.,t)-z) - E[k]/(z_type(-1.,t)-z) );}   
  cu=.5-I/(2.*M_PI)*log( (z_type(1.,-A)+z)/(z_type(1., A)-z) );
  cd=.5-I/(2.*M_PI)*log( (z_type(1.,-A)-z)/(z_type(1., A)+z) );
  c=c*(A/(2.*M_PI)) +Zo*cu+Zc*cd;
  if(abs(n-K/2)<4)printf("%3d %6.3f  %9.6f %9.6f  %9.6f %9.6f\n",n,y,Re(F[n]),Im(F[n]),Re(c),Im(c));
  E[n]=log(c)/a; F[n]=c; G[n]=exp(c*a);}
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Re(F[k]);if(j==0)M(y,u)else L(y,u)}
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Im(F[k]);if(j==0)M(y,u)else L(y,u)}
fprintf(o,".01 W 1 0 0 RGB S\n");
for(n=K-1;n>0;n-=2)
{y=GLx[n]*A; z=z_type(0.,y); c=0.;  //printf(" %3d",n);
 DO(k,K){t=A*GLx[k]; c+= GLw[k]*( G[k]/(z_type( 1.,t)-z) - E[k]/(z_type(-1.,t)-z) );}	
 cu=.5-I/(2.*M_PI)*log( (z_type(1.,-A)+z)/(z_type(1., A)-z) );
 cd=.5-I/(2.*M_PI)*log( (z_type(1.,-A)-z)/(z_type(1., A)+z) );
 c=c*(A/(2.*M_PI)) +Zo*cu+Zc*cd;
 if(abs(n-K/2)<4)printf("%3d %6.3f  %9.6f %9.6f  %9.6f %9.6f\n",n,y,Re(F[n]),Im(F[n]),Re(c),Im(c));
 E[n]=log(c)/a;  F[n]=c;  G[n]=exp(c*a); }
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Re(F[k]);if(j==0)M(y,u)else L(y,u)}
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Im(F[k]);if(j==0)M(y,u)else L(y,u)}
fprintf(o,".02 W 0 1 0 RGB S\n");
for(n=0;n<K;n+=2)
{y=GLx[n]*A; z=z_type(0.,y); c=0.;  //printf(" %3d",n);
 DO(k,K){t=A*GLx[k]; c+= GLw[k]*( G[k]/(z_type( 1.,t)-z) - E[k]/(z_type(-1.,t)-z) );}	
 cu=.5-I/(2.*M_PI)*log( (z_type(1.,-A)+z)/(z_type(1., A)-z) );
 cd=.5-I/(2.*M_PI)*log( (z_type(1.,-A)-z)/(z_type(1., A)+z) );
 c=c*(A/(2.*M_PI)) +Zo*cu+Zc*cd;
 if(abs(n-K/2)<4)printf("%3d %6.3f  %9.6f %9.6f  %9.6f %9.6f\n",n,y,Re(F[n]),Im(F[n]),Re(c),Im(c));
 E[n]=log(c)/a; F[n]=c; G[n]=exp(c*a);	}
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Re(F[k]);if(j==0)M(y,u)else L(y,u)}
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Im(F[k]);if(j==0)M(y,u)else L(y,u)}
fprintf(o,".01 W 0 0 1 RGB S\n");
for(n=K-1;n>0;n-=2)
{y=GLx[n]*A; z=z_type(0.,y); c=0.;  //printf(" %3d",n);
 DO(k,K){t=A*GLx[k]; c+= GLw[k]*( G[k]/(z_type( 1.,t)-z) - E[k]/(z_type(-1.,t)-z) );}	
 cu=.5-I/(2.*M_PI)*log( (z_type(1.,-A)+z)/(z_type(1., A)-z) );
 cd=.5-I/(2.*M_PI)*log( (z_type(1.,-A)-z)/(z_type(1., A)+z) );
 c=c*(A/(2.*M_PI)) +Zo*cu+Zc*cd;
 if(abs(n-K/2)<4)printf("%3d %6.3f  %9.6f %9.6f  %9.6f %9.6f\n",n,y,Re(F[n]),Im(F[n]),Re(c),Im(c));
 E[n]=log(c)/a; F[n]=c; G[n]=exp(c*a);}
DO(j,4)
{
 for(n=0;n<K;n+=2)
 { y=GLx[n]*A; z=z_type(0.,y); c=0.;  //printf(" %3d",n);
   DO(k,K){t=A*GLx[k]; c+= GLw[k]*( G[k]/(z_type( 1.,t)-z) - E[k]/(z_type(-1.,t)-z) );}	
   cu=.5-I/(2.*M_PI)*log( (z_type(1.,-A)+z)/(z_type(1., A)-z) );
   cd=.5-I/(2.*M_PI)*log( (z_type(1.,-A)-z)/(z_type(1., A)+z) );
   c=c*(A/(2.*M_PI)) +Zo*cu+Zc*cd;
   if(abs(n-K/2)<2)printf("%3d %6.3f  %9.6f %9.6f  %9.6f %9.6f\n",n,y,Re(F[n]),Im(F[n]),Re(c),Im(c));
   E[n]=log(c)/a; F[n]=c; G[n]=exp(c*a);	}
 for(n=K-1;n>0;n-=2)
 { y=GLx[n]*A; z=z_type(0.,y); c=0.;  //printf(" %3d",n);
   DO(k,K){t=A*GLx[k]; c+= GLw[k]*( G[k]/(z_type( 1.,t)-z) - E[k]/(z_type(-1.,t)-z) );}	
   cu=.5-I/(2.*M_PI)*log( (z_type(1.,-A)+z)/(z_type(1., A)-z) );
   cd=.5-I/(2.*M_PI)*log( (z_type(1.,-A)-z)/(z_type(1., A)+z) );
   c=c*(A/(2.*M_PI)) +Zo*cu+Zc*cd;
   if(abs(n-K/2)<2)printf("%3d %6.3f  %9.6f %9.6f  %9.6f %9.6f\n",n,y,Re(F[n]),Im(F[n]),Re(c),Im(c));
   E[n]=log(c)/a; F[n]=c; G[n]=exp(c*a);}
}
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Re(F[k]);if(j==0)M(y,u)else L(y,u)}
DO(j,440){k=K/2+j-220; y=GLx[k]*A; u=Im(F[k]);if(j==0)M(y,u)else L(y,u)}
fprintf(o,".01 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n\%c%cTrailer",'%','%'); fclose(o); 
system("epstopdf TetSheldonIma.eps");
system(    "open TetSheldonIma.pdf");
o=fopen("TetSheldonIma.inc","w");
fprintf(o,"z_type F[K]={\n");
DO(k,K-1) fprintf(o,"z_type(%19.16lf,%19.16lf),\n",Re(F[k]),Im(F[k]));
          fprintf(o,"z_type(%19.16lf,%19.16lf)};\n",Re(F[K-1]),Im(F[K-1]));
fclose(o);
}

Latex generator of lables

\documentclass[12pt]{article} % \paperwidth 2100pt % \paperheight 472pt % \textwidth 2060pt % \textheight 500pt % \topmargin -100pt % \oddsidemargin -104pt % \pagestyle{empty} % \usepackage[usenames]{color} % \usepackage[utf8x]{inputenc} % \usepackage{hyperref} % \usepackage{graphicx} % \usepackage{rotating} % \newcommand \sx {\scalebox} % \newcommand \ing {\includegraphics} % \newcommand \rme {\mathrm{e}} % \newcommand \rot {\begin{rotate}} % \newcommand \ero {\end{rotate}} % \begin{document} % \parindent 0pt % \begin{picture}(2090,432) % \put(-10,10){\ing{TetSheldonIma}} % \put(50,392){\sx{5}{$2$}} % \put(50,293){\sx{5}{$1$}} % \put(50,194){\sx{5}{$0$}} % \put(23,94){\sx{5}{$-\!1$}} % \put(23,-6){\sx{5}{$-\!2$}} % \put(250,-28){\sx{4.5}{$-8$}} % \put(450,-28){\sx{4.5}{$-6$}} % \put(650,-28){\sx{4.5}{$-4$}} % \put(850,-28){\sx{4.5}{$-2$}} % \put(1084,-28){\sx{4.5}{$0$}} % \put(1284,-28){\sx{4.5}{$2$}} % \put(1484,-28){\sx{4.5}{$4$}} % \put(1684,-28){\sx{4.5}{$6$}} % \put(1884,-28){\sx{4.5}{$8$}} % \put(2084,-28){\sx{4.5}{$x$}} % \put(220,394){\sx{4.2}{$\Im\big(f(x)\big)$}} % \put(220,32){\sx{4.2}{$\Re\big(f(x)\big)$}} % \put(1800,377){\sx{4.2}{$\Im\big(f(x)\big)$}} % \put(1800,290){\sx{4.2}{$\Re\big(f(x)\big)$}} % \end{picture} % \end{document}

Related pictures

The same algorithm is used for the evaluation of tetration to the natural base ($b\!=\!\mathrm e$) ^[2].

Keywords

Tetration, Tetration to Sheldon base. Filog, Superfunction

References

↑ http://en.citizendium.org/wiki/Legendre-Gauss_Quadrature_formula
↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane.. Mathematics of Computation, 78: 1647-1670

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	17:50, 20 June 2013		4,359 × 980 (598 KB)	Maintenance script (talk \| contribs)	Importing image file

You cannot overwrite this file.

File usage

The following page uses this file:

Iterated Cauchi

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Horizontal resolution	59.06 dpc
Vertical resolution	59.06 dpc

[czlg-1] ttp://en.citizendium.org/wiki/Legendre-Gauss_Quadrature_formula

[mcom1-2] ttp://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of F(z+1)=exp(F(z)) in the complex plane.. Mathematics of Computation, 78: 1647-1670

[1]

[2]