MapConrec6demo
MapConrec6demo is technical article; it is collection of pictures created as demonstration of use of routine «Conrec6.cin».
That routine is designed by ChatGPT and Dmitrii Kousnetsov (2025) for generation of Complex maps.
Routine «Conrec6.cin» is created as modern substitute of the earlier and "dirty" routine «conto.cin» from Citizendium [1].
The contouring subroutine "Conrec" [2] is used as a prototype for the new version «Conrec6.cin».
The compilation of C++ file with that routine requires options "-std=c++11 -O2"
The routine «Conrec6.cin» is still under testing.
However, you may use it for your own risk.
Attribute the source; indicate your modifications, if any.
This helps to trace errors, if any.
The generators are supplied in descriptions of the pictures (click on the picture).
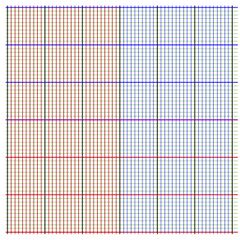
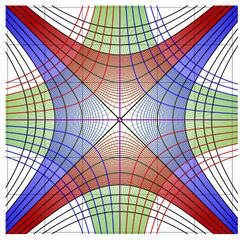
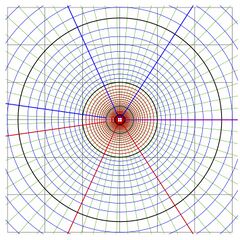
The first four functions shown below are trivial elementary functions.
Pics
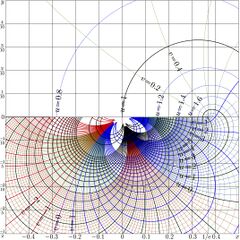
Maps of the following functions are shown below: \(z\!\mapsto\! z\) (Identity function), \(z\!\mapsto\! z^2\), \(z\!\mapsto\! \log(z)\), \(z\!\mapsto\! \sqrt{z}\), \(z\!\mapsto\! \)Filog\((z)\).
in each case, function \(z\!\mapsto\! f(z)\) is shown with lines of constant its real part and lines of constant its imaginary part: \[ u + \mathrm i v = f(x\!+\!\mathrm i y) \]
Lines \(u = \mathrm{const} \) and
lines \(v = \mathrm{const} \) are drawn.
Integer values of \(u\) and \(v\)
are drawn with thick lines.
The thin lines are drawn with step 1/10.
Integer values of \(u\) are shown with black thick lines.
Positive integer values of \(v\) are shown with blue thick lines. Negative integer values of \(v\) are shown with red thick lines. Isoline \(v\!=\!0\) is shown with dark pink thick line.
Other (non-integer) values of \(v\) are shown with dark green thin lines.
Non-integer positive values of \(u\) are shown with thin blue lines.
Non-integer negative values of \(u\) are shown with thin red lines.
This style is used in the majority of complex maps loaded at TORI and, in particular for those that are used in book Superfunctions[3].
In the first four pictures, in order to keep them simple, the labels are not added. The grid lines are drown from -3 to 3 with step unity (not to be confused with step of the mesh) both alone the real axis and along the imaginary axis.
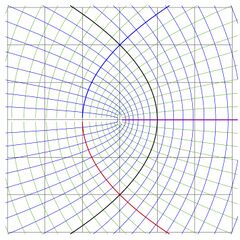
The in the fifth picture, the grid lines are drawn with step 0.1; the labels are added.
Function Filog is implemented for the fast evaluation of two fixed points of logarithm
with single routine.
The map reproduces the bottom part of Fig.18.2 at page 248 of book
«Superfunctions»[3][4], 2020.
The original is generated with historic routine conto.cin [1];
it is shown as the 6th picture.
The 5th and 6th pictures use the same set of labels;
and the contour lines look identical;
it is very difficult to see any difference between these two pictures;
they look the same.
Warnings
Routine Conrec6 is still under testing.
You may get the preliminary version from the description of any of pictures above or from article «Conrec6.cin» and use at your own risk.
Attribute the source and your modification(s) if any.
This helps to trace errors, if any.
The numbering of versions of the routine in TORI is not yet established.
The “6” in name «Conrec6.cin» refers to the 6-digit precision used for EPS output coordinates, not to version numbering.
Even ChatGPT got confused with this "6". Sorry about the naming.
If you make a new version of the routine to plot complex maps,
better than «conto.cin» and better than «Conrec6.cin»,
choose a better name for it.
References
- ↑ 1.0 1.1 https://en.citizendium.org/wiki/Contour_plot/Code/conto.cin // Copyleft 2008 by Dmitrii Kouznetsov This page was last modified 01:05, 2 February 2009.
- ↑ https://paulbourke.net/papers/conrec/ CONREC // A Contouring Subroutine // Written by Paul Bourke // July 1987 // Source code
- ↑ 3.0 3.1 http://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetov. Superfunctions 2020.
- ↑ https://www.morebooks.de/shop-ui/shop/product/978-620-2-67286-3 Superfunctions // Non-integer iterates of holomorphic functions. Tetration and other superfunctions Formulas,algorithms,tables,graphics // 978-620-2-67286-3 // Tools for evaluation of superfunctions, abelfunctions and non-integer iterates of holomorphic functions are collected. For a given transferfunction T, the superfunction is solution F of the transfer equation F(z+1)=T(F(z)) . The abelfunction is inverse of F. In particular, superfunctions of factorial, exp, sin are suggested. The Holomorphic extensions of the logistic sequence and those of the Ackermann functions are considered. Among ackermanns, the tetration (mainly to the base b>1) and natural pentation (to base b=e) are presented. The efficient algorithm for the evaluation of superfunctions and abelfunctions are described. The graphics and complex maps are plotted. The possible applications are discussed. Superfunctions significantly extend the set of functions, that can be used in scientific research and technical design. Generators of figures are loaded to http://mizugadro.mydns.jp/BOOK for the free downloading. With these generators, the Readers can reproduce (and modify) the figures from the Book. The Book is intended to be applied and popular. I try to avoid the complicated formulas, but some knowledge of the complex arithmetics and the Cauchy integral should help.// Authors Dmitrii Kouznetsov // Book language English Published on 2020-07-28 Publishing house LAP LAMBERT Academic Publishing Number of pages 328 Price (EUR ) €52.90
Keywords
«Ado.cin», «ChatGPT», «Complex map», «Conrec6», «Conrec6 demo», «Conrec6.cin», «conto.cin», «Filog», «Filog.cin», «MapConrec6demo», «LogTestMaps»,