File:KellerPlotT.png

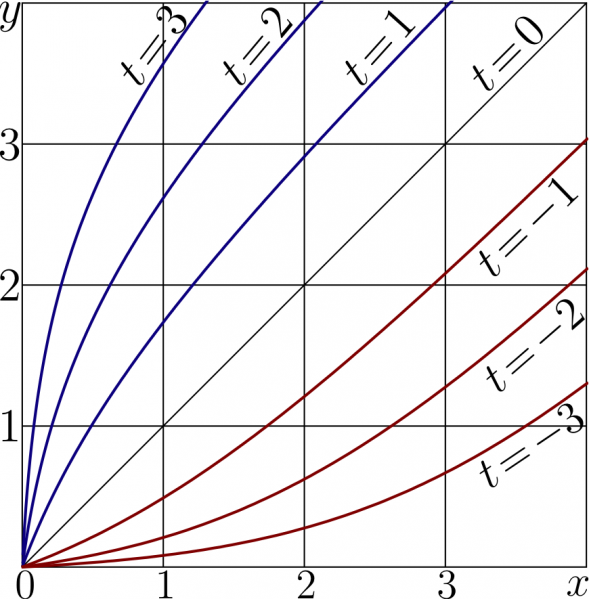
Explicit plot of various iterations $t$ the Keller function

$ y=\mathrm{Keller}^t(x)=\mathrm{Shoka}\Big( t + \mathrm{ArcShoka}(x)\Big)$

To plot this graphic, the iterations of the Keller function are implemented through the Shoka function and the ArcShoka function.

C++ generator of curves]]

// File ado.cin shold be loaded to the working directory in order to compile the C++ code below.

#include <math.h> 
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)

#include"ado.cin"

z_type Shoka(z_type  z)  { return z + log(exp(-z)+(M_E-1.)); }
z_type ArcShoka(z_type z){ return z + log((1.-exp(-z))/(M_E-1.)) ;}  

#define M(x,y) fprintf(o,"%6.3f %6.3f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.3f %6.3f L\n",0.+x,0.+y);
main(){ int j,k,m,n; DB x,y, a;
FILE *o;o=fopen("KellerPlot.eps","w");ado(o,408,412);
fprintf(o,"4 4 translate\n 100 100 scale 2 setlinecap 1 setlinejoin\n");
for(m=0;m<5;m++){ M(m,0)L(m,4)}
for(n=0;n<5;n++){ M(0,n)L(4,n)}
M(0,0)L(4,4)
fprintf(o,".01 W 0 0 0 RGB S\n");
DO(n,134){x=.005+.01*n;y=Re(Shoka(3.+ArcShoka(x)));if(n==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 0 .5 RGB S\n");
DO(n,216){x=.005+.01*n;y=Re(Shoka(2.+ArcShoka(x)));if(n==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 0 .5 RGB S\n");
DO(n,154){x=.005+.02*n;y=Re(Shoka(1.+ArcShoka(x)));if(n==0)M(x,y)else L(x,y)} fprintf(o,".02 W 0 0 .5 RGB S\n");
DO(n,101){x=.005+.04*n;y=Re(Shoka(-1.+ArcShoka(x)));if(n==0)M(x,y)else L(x,y)} fprintf(o,".02 W .5 0 0 RGB S\n");
DO(n,101){x=.005+.04*n;y=Re(Shoka(-2.+ArcShoka(x)));if(n==0)M(x,y)else L(x,y)} fprintf(o,".02 W .5 0 0 RGB S\n");
DO(n,101){x=.005+.04*n;y=Re(Shoka(-3.+ArcShoka(x)));if(n==0)M(x,y)else L(x,y)} fprintf(o,".02 W .5 0 0 RGB S\n");
fprintf(o,"showpage\n%cTrailer",'%'); fclose(o);
    system("epstopdf KellerPlot.eps");
    system(    "open KellerPlot.pdf"); //these 2 commands may be specific for macintosh
getchar(); system("killall Preview");// if run at another operational sysetm, may need to modify
}

Latex generator of labels

% File KellerPlot.pdf should be generated with the code above in order to compile the Latex document below.

% \documentclass[12pt]{article} %<br> \usepackage{geometry} %<br> \usepackage{graphicx} %<br> \usepackage{rotating} %<br> \paperwidth 419pt %<br> \paperheight 426pt %<br> \topmargin -103pt %<br> \oddsidemargin -83pt %<br> \textwidth 1200pt %<br> \textheight 600pt %<br> \pagestyle {empty} %<br> \newcommand \sx {\scalebox} %<br> \newcommand \rot {\begin{rotate}} %<br> \newcommand \ero {\end{rotate}} %<br> \newcommand \ing {\includegraphics} %<br> \begin{document} %<br> \sx{1}{ \begin{picture}(810,410) %<br> \put(1,9){\ing{KellerPlot}} % <br> \put(-12,401){\sx{2.8}{$y$}} % <br> \put(-12,303){\sx{2.8}{$3$}} % <br> \put(-12,203){\sx{2.8}{$2$}} % <br> \put(-12,103){\sx{2.8}{$1$}} % <br> \put(0,-9){\sx{2.5}{$0$}} % <br> \put(100,-9){\sx{2.5}{$1$}} % <br> \put(200,-9){\sx{2.5}{$2$}} % <br> \put(300,-9){\sx{2.5}{$3$}} % <br> \put(392,-7){\sx{2.6}{$x$}} % <br> %\put(560,214){\rot{37}\sx{4}{$y=\mathrm{Tania}(x)$}\ero} % <br> \put( 88,354){\rot{53}\sx{2.8}{$t\!=\!3$}\ero} %<br> \put(160,354){\rot{50}\sx{2.8}{$t\!=\!2$}\ero} %<br> \put(246,354){\rot{48}\sx{2.8}{$t\!=\!1$}\ero} %<br> \put(336,350){\rot{45}\sx{2.8}{$t\!=\!0$}\ero} %<br> \put(340,218){\rot{44}\sx{2.8}{$t\!=\!-1$}\ero} %<br> \put(344,136){\rot{41}\sx{2.7}{$t\!=\!-2$}\ero} %<br> \put(338, 68){\rot{34}\sx{2.7}{$t\!=\!-3$}\ero} %<br> \end{picture} %<br> } %<br> \end{document} %

Copyleft status

Copyleft 2012 by Dmitrii Kouznetsov. The image and the generators above may be used for free; attribute the source.

Refernces