Keller function

Ursula Keller

Iterates of the Keller function: \(y\!=\!\mathrm{Keller}^t(x)\)

\(u\!+\!\mathrm i v=\mathrm {Keller}(x\!+\!\mathrm i y)\)

\(u\!+\!\mathrm i v=\mathrm {ArcKeller}(x\!+\!\mathrm i y)\)

Keller function (Функция Келлер) is elementary function defined with

\(\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \mathrm{Keller}(z)=z+ \ln\!\Big(\mathrm e - \mathrm e^{-z}(\mathrm e-1) \Big)\)

The Keller function describes the transfer of the pulse in the simple model of the laser medium with unsaturated gain unity. The function is called after Ursula Keller , as she describes it in her publications.

Keller function is used as example in book Superfunctions .

Definition and representations

For moderate values of the imaginary part of the argument, the Keller function can be expressed in the way, closer to that it appears in the literature on the laser science

\(\!\!\!\!\!\!\!\!\!\! (2) ~ ~ ~ \mathrm{Keller}_0(z)=\ln\Big( 1+ \mathrm e \, (\mathrm e^z -1) \big)\)

In this case, \(z\) may have sense of normalized fluence of the optical pulse at the input of the laser amplifier; then \(\mathrm{Keller}(z)\) is the output fluence measured in the same unit.

In the strip \(|\Im(z)|<\pi\), functions Keller and Keller\(_0\) are equivalent, \(\mathrm{Keller}(z)=\mathrm{Keller}_0(z)\).

However, in TORI, \(z\) may be considered also as just a complex variable; so, the Keller is treated as just holomorphic function of complex argument.

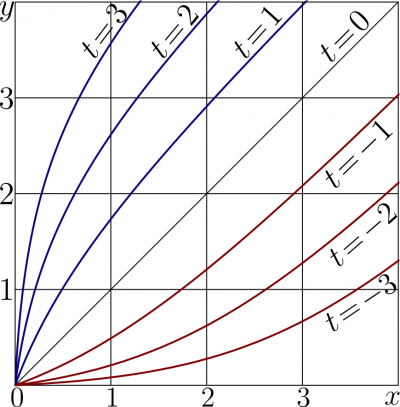
Keller is analogy of the Doya function for the case of amplification of short pulses, while Doya describes the amplification of the cw signal in the laser medium with simple kinetics. Various iterates of the Keller function are plotted in figure at right.

Numerical implementation

As the Keller is expressed through elementary functions, no special numerical implementation is required. However, in order to avoid the loss of precision, at small values of the argument the expansion can be used:

\( \displaystyle \mathrm{Keller}(z)=\mathrm e z-\frac{\mathrm e\,(\mathrm e-1)}{2} z^2+O(z^3)\)

Refular iteration for superfunction of Keller

Treating the Keller function as transfer function the regular iteration, the superfunction \(F\) can be constructed with asymptotic behavior

\( F(z)=\mathrm e^z - \frac{1}{2}\mathrm e^{2z} + O(\mathrm e^{3z})\)

This superfunncion corresponds to the displacement of the argument for \(\log(\mathrm e \!-\!1)\) of the Shoka function discussed below.

Shoka function

The Keller function may have sense of the transfer function. One of superfunctions of the Keller function is called Shoka function,

\(\!\!\!\!\!\!\!\!\!\! (12) ~ ~ ~ \mathrm{Shoka}(z)=z+\ln\Big( (\mathrm e\!-\!1) + \mathrm e^{-z} \big)\)

In this case, \(z\) may have sense of length of the amplifier, measured in units of inverse of unsaturated gain.

However, \(z\) in (12) may be considered also as just a complex variable; so, in TORI, the Shoka function is treated as holomorphic function of complex argument.

The inverse function of the Shoka can be expressed as follows:

\(\!\!\!\!\!\!\!\!\!\! (13) ~ ~ ~ \displaystyle \mathrm{ArcShoka}(z)= z + \ln\!\left( \frac{\mathrm 1-\mathrm e^{-z}}{\mathrm e-1} \right)\)

Specific values: \(\mathrm{Shoka}(0)=1\); \(\mathrm{ArcShoka}(1)=0\)

Shoko function

Along the real axis and its vicinity, the Shoka function coincides with the Shoko function

\(\!\!\!\!\!\!\!\!\!\! (22) ~ ~ ~ \mathrm{Shoko}(z)=\ln\Big( 1+\mathrm e^z\, (\mathrm e-1) \big)\)

In particular, for real values of the atgument, equation (22) can be used instead of (12). As the argument of the Shoko function is used in (2) only once, the calculation of the inverse function is straightforward:

\(\!\!\!\!\!\!\!\!\!\! (23) ~ ~ ~ \displaystyle \mathrm{ArcShoko}(z)=\ln \left( \frac{\mathrm e^z -1}{\mathrm e - 1} \right) \)

Specific values are the same as in the case of the Shoko function,

\(\mathrm{Shoko}(0)=1\); \(\mathrm{ArcShoko}(1)=0\)

Iteration of the Keller function

Using Shoka and ArcShoka, the \(t\)th iterate of the Keller function can be expressed as follows:

\(\!\!\!\!\!\!\!\!\!\! (34) ~ ~ ~ \mathrm{Keller}^t(z)=\mathrm{Shoka}\Big(t+\mathrm{ArcShoka}(z)\Big)\)

In vicinity of the real axis, the iterates of the Keller function can be expressed also through the Shoka function

\(\!\!\!\!\!\!\!\!\!\! (35) ~ ~ ~ \mathrm{Keller}^t(z)=\mathrm{Shoka}\Big(t+\mathrm{ArcShoka}(z)\Big)= \ln\!\Big(1+\mathrm e^t(\mathrm e^z\!-\!1)\Big) \)

Parameter \(t\) may have sense of the length of the amplifier, measured in units of the inverted insaturated gain; then, the argument and value of \(\mathrm {Keller}^t\) have sense of the input and output fluence, measured in units of the saturation.

In particular, the inverse function of Keller can be expressed in the usual way,

\(\!\!\!\!\!\!\!\!\!\! (36)\displaystyle ~ ~ ~ \mathrm{ArcKeller}(z)=\mathrm{Keller}^{-1}(z)= z+\ln\!\left( \frac{1}{\mathrm e}+\frac{\mathrm e \!-\!1}{\mathrm e}\, \mathrm e^{-z} \right)\)

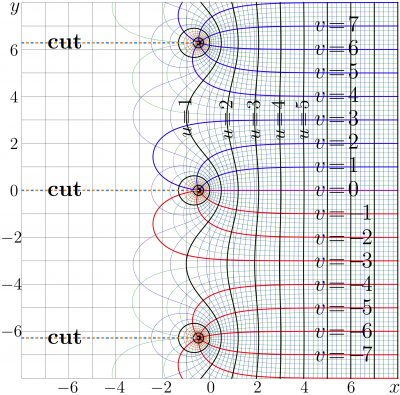
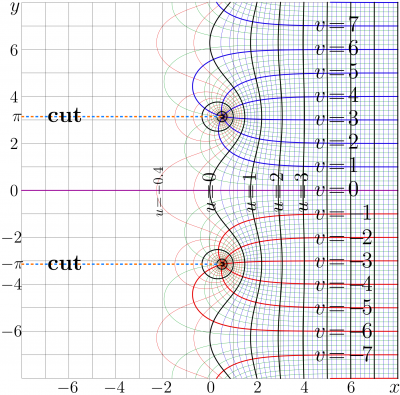
The complex map of the ArcKeller function is shown in figure at right.

Doya function

Transfer functions of laser amplifiers with simple kinetics for the short pulses (Keller function) and for the continuous-wave operation (Doya function)

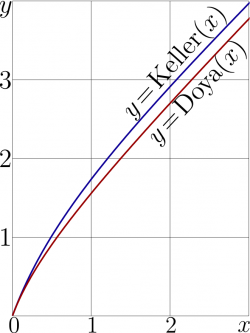
The Keller function describes the amplification of the short pulses in a laser medium with unsaturated gain unity, id est, with coefficient of amplivication of small signal equal to the base of natural logarithm; the simple two–level model for the kinetics of the excitations is used. In this case, the argument of the Keller function is fluence at the input, normalized for the saturation fluence.

Similar transfer function can be obtained within the same model for the amplification of continuous waves; in TORI it is called Doya function. The argument of this function may have sense of the input intensity, measured in units of the saturation intensity; and the returned value corresponds to the output intensity in the same units.

Figure at right shows the comparison of the Keller function to the Doya function for real values of the argument. The curves look similar. At the poor experimental data available in the literature, usually it is difficult to guess, which function would better fit the data – the Doya function or the Keller function, id est, to distinguish, do the data correspond to the continuous wave operation or to amplification of the short pulses. (Perhaps the same experimental dots could be claimed to be as results of measuremens for pulses and those for the continuous-wave operation.) The precise measurements of the transfer function would allow not only to distinguish the cases with continuous-wave from those with short pulses, but also to see the limits of applicability of the model of a laser medium and choose between various models.

Etymology of names

Expression, similar to the Keller function, appears in the papers by R.Paschotta and U.Keller and by M.Haiml, R.Grange and U.Keller . Among the authors, the name Keller seems to be easier to pronounce.

Yulya had indicated that the Keller function may be good example of realistic transfer function, and the name for the superfunction was urgently needed. Name Yulya function is already occupied (for the dependence, that has application in the interferometric microscopy), so, the superfunction should have another name. Shoko agreed that her name will be used as name of the superfunction for the Keller function. Name Shoka function is modification of the Shoko function, such modification become necessary when it happens that the cutlines of the Shoko function go to the right hand side, which in not right in the sense that by default, in TORI all the cut lines should be directed to the left, in order to provide the holomorphizm in the right–hand side of the complex plane (if possible). Then, the Shoka function became the principal, main version of that function, and the Shoko function is the alternative, necessary for the allowance with the shape it appears in the literature about the Laser science.

If the specialists on the history of laser science find, that another name(s) are more suitable for the functions Keller and Shoko, let them describe these functions with other names, and bring to TORI the link, in order to cite those descriptions here and indicate the alternative names.

Keywords

Shoko function, Transfer function, Laser science,