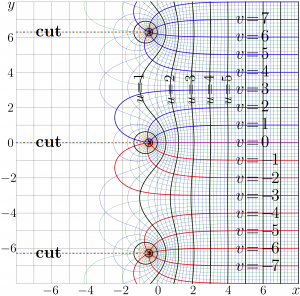
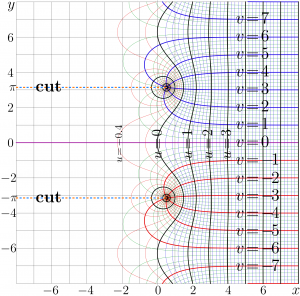
ArcKeller

\(u\!+\!\mathrm i v\!=\! \mathrm{Keller}(x\!+\!\mathrm i \mathrm y)\)

\(u\!+\!\mathrm i v\!=\! \mathrm{ArcKeller}(x\!+\!\mathrm i \mathrm y)\)

ArcKeller appers as inverse function of the Keller function; there exist the explicit representations for these functions through the elementary functions:

\(\!\!\!\!\!\!\!\!\!\! (1) ~ ~ ~ \mathrm{Keller}(z)=z+ \ln\!\Big(\mathrm e - \mathrm e^{-z}(\mathrm e-1) \Big)\)

\(\!\!\!\!\!\!\!\!\!\! (2)\displaystyle ~ ~ ~ \mathrm{ArcKeller}(z)=\mathrm{Keller}^{-1}(z)= z+\ln\!\left( \frac{1}{\mathrm e}+\frac{\mathrm e \!-\!1}{\mathrm e}\, \mathrm e^{-z} \right)\)

It is amazing, that, in general,

\(\!\!\!\!\!\!\!\!\!\! (3) ~ ~ ~ \mathrm{ArcKeller}(z+1+\pi \mathrm i)= \mathrm{Keller}(z) -1 + \pi \mathrm i\)

The complex maps of the Keller function and the ArcKeller function are shown in figure at right.

The ArcKeller function may be considered as the minus first iteration of the Keller function; in general, the \(t\)th iteration of the Keller function can be written as follows:

\(\!\!\!\!\!\!\!\!\!\! (4)\displaystyle ~ ~ ~ \mathrm{Keller}^t(z)= z+t+\ln\!\Big(1-\mathrm e^{-z}(1-\mathrm e^{-t}) \Big)\)

The iterates of the Keller function, and, in particular, the ArcKeller function appear as the transfer function at the amplification of short optical pulses in the gain medium with simple model of kinetics of excitation of the active centers. Then, the argument of the ArcKeller may have sense of the fluence of the input pulse, measured in units of the saturation fluence. Value of the funcction have sense of the output fluence, measured in the same units, assuming, that the absorption of a weak pulse is just \(\mathrm e=\exp(-1)\). The transfer function of the arbitrary thick amplifier of absorber appears as corresponding iteration of the ArcKeller or the Keller function. The arbitrary iteration number \(t\) of the Keller function (4) can be expressed also in terms of the ArcShoka and Shoka functions, as they are superfunction and Abel function of the Keller function:

\(\!\!\!\!\!\!\!\!\!\! (5)\displaystyle ~ ~ ~ \mathrm{Keller}^t(z)= \mathrm{Shoka}\Big(t+\mathrm{ArcShoka}(z)\Big)\)

In particular, at \(t=-1\) equation (5), as well as equation (4), gives the ArcKeller function. In (5), both ArcShoka and Shoka functions can be expressed in terms of elementary functions:

\(\!\!\!\!\!\!\!\!\!\! (6)\displaystyle ~ ~ ~ \mathrm{Shoka}(z)=z+\ln\Big( (\mathrm e\!-\!1) + \mathrm e^{-z} \big)\)

\(\!\!\!\!\!\!\!\!\!\! (7)\displaystyle ~ ~ ~ \mathrm{ArcShoka}(z)= z + \ln\!\left( \frac{\mathrm 1-\mathrm e^{-z}}{\mathrm e-1} \right)\)

The ArcKeller and the Keller functions are examples of the realistic transfer functions, that can be realized at the optical bench and still allow the Abel functions and the Superfunctions in terms of the elementary functions. Expressions, analogous to the iterations of the Keller function, appeared in publications by U.Keller . For this reason, this name is used in TORI to call the function.

Keywords

Keller function, Shoka function, ArcShoka, Transfer function, Laser science