ArcCip

complex map of $u+\mathrm i v=\mathrm{Cip}(x+\mathrm i y)$

complex map of $u+\mathrm i v=\mathrm{ArcCip}(x+\mathrm i y)$

Cip$=$cosc is elementary function constructed through the Cos function:

$\displaystyle \mathrm {Cip}(z)=\frac{\cos(z)}{z}$

ArcCip$=$ArcCosc is the inverse function, id est, solution of equation

$\displaystyle \mathrm{Cip}(\mathrm{ArcCip}(z))=z$.

Instead of ArcCip, notation ArcCosc seems to be better.

Notations

In analogy with ArcCos, with is denoted also as acos or ACos, the name ACip is also used; ACip=ArcCip.

After to load this article, it happened, that inverse function of sinc, id est, $\mathrm{sinc}(z)=\sin(z)/x$ also has application int he atom optics. The name of function sinc is already well established. For this reason, the natural chose for the name of function Cip is cosc, and natural name of the inverse function if arccosc=ArcCosc.

The article ArcCosc is suggested to be used instead of this article. The content is mainly the same, but this article is not updated and the ArcCosc is more advanced.

Real argument

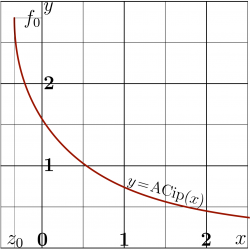
Explicit plot $y=\mathrm{ArcCip}(x)$ is shown in left figure for real values of argument $x$. The same figure can be interpreted as implicit plot $(\mathrm{Cip}(y),y)$. (In such a way, the figure could be generated without numerical implementation of ArcCip). However, for the application to the channeling of particles by the absorbing walls, the efficient implementation for ArcCip is required, and this implementation is used to plot the complex map. Complex maps

$f=\mathrm{Cip}(x+\mathrm i y) ~ ~$ and

$f=\mathrm{ArcCip}(x+\mathrm i y)~$

are shown in figures at right with lines $u\!=\!\Re(f)\!=\!\mathrm{const}$ and lines $v\!=\!\Im(f)\!=\!\mathrm{const}$

Expansion at large values of the argument

At small values of argument funcion Cip expands as follows:

$\displaystyle \mathrm{Cip}(z) = \frac{1}{z} -\frac{z}{2}+\frac{z^3}{24}+\frac{z^5}{720}+...~$, $~ |z|\!\ll\! 1$

This gives the expansion of ArcSip at large values of the argument:

$\displaystyle \mathrm{ArcCip}(z) = \frac{1}{z} -\frac{1}{2z^3}+\frac{13}{24z^5}-\frac{541}{720z^7}+...$ , $~ \Re(z)\!>\!0~,~~ |z|\!\gg\! 1$

This expansion is used to approximate $\mathrm{ArcCip}(z)$ for $\Re(z)\!>\!0$, $|z|\gg 1$.

Expansion at the real branch point

Equation $\mathrm{Cip}'(z)=0$ has several solutions. One of them is $z=f_0\approx 2.798386045783887$ .

$\mathrm{Cip}'(f_0)\!=\!0~$,

Denote value of Cip at this point with $x_0$, id est,

$ x_0=\mathrm{Cip}(f_0)\approx -0.33650841691839534$

Function Cip can be expanded as follows:

$\mathrm{Cip}(f_0+t)=x_0+b_2 t^2+ b_3 t^3 +b_4 t^4 + ...$

with

$b_2 \approx 0.16825420845919767$

$b_3 \approx 0.040083630518072705$

$b_4 \approx 0.00030265472531785555$

$x_0$ is branch point ArcCip, and ArcCip can be expanded as follows:

$\mathrm{ArcCip}(x_0+t)=f_0 + c_1 \sqrt{z-x_0} +c_2 (z-x_0) + c_3 (z-x_0)^{3/2} + ...$

the coefficients $b$ can be evaluated inverting the expansion for Cip, that gives

$c_1 \approx 2.437906425896532$

$c_2 \approx 0.7079542331649882$

$c_3 \approx 0.5009330133042798$

The radios of convergence is determined by the distance to another nearest singularity and is of order of unity. In particular, this expansion can be used for evaluation of ArcCip at small values of argument, $|z|\ll 1$.

Expansion at the imaginary branch point

Equation $\mathrm{Cip}'(z)=0$ has also pure imaginary solutions

$z=f_0 \approx \, - 1.1996786402577337 ~ \rm i$

and

$z=f_0^* \approx \! 1.1996786402577337 ~ \rm i$

At $f_0$ function Cip can be expanded as follows:

$ \mathrm{Cip}(f_0+t) = z_0 + z_2 t^2 + z_3 t^3 +z_4 t^4 +..$

where

$ z_0 \approx ~ ~ 1.50887956153832 \, \mathrm{i} $

$ z_2 \approx -0.7544397807691602 \, \mathrm{i}$

$ z_3 \approx -0.4192454853893649 $

$ z_4 \approx ~ ~ 0.41233480616015905 \, \mathrm{i}$

and at point $z_0$, function ArcCip can be expanded as follows:

$\mathrm{Cip}(z_0+t)= f_0 + f_1 t^{1/2} +f_2 t + f_3 t^{3/2} +..$

where

$ f_0 \approx -1.199678640257734 \, \mathrm{i}$

$ f_1 \approx 0.8140905473896508 + 0.8140905473896508 \mathrm{i}$

$ f_2 \approx -0.4192454853893649 $

$ f_3 \approx 0.08661404692621909 - 0.08661404692621909\, \mathrm{i}$

$ f_4 \approx -0.1109114793294265` \mathrm{i}$

In such a way, $z_0$ and $z_0^*$ are branch points of function ArcCip.

Cih and ArcCih

Warning! The expansions in this section are still under revision!

However, the expansion at imaginary values of argument can be done in more intelligent way. Let

$ \mathrm{Cih}(z) = \mathrm{i}~ \mathrm{Cip}(\mathrm i z)$

then

$ \mathrm{Cip}(z) = \mathrm{i}~ \mathrm{Cih}(\mathrm i z)$

Cih is also real-holomorphic,

$ \displaystyle \mathrm{Cih}(z) = \frac{\cosh(z)}{z}$

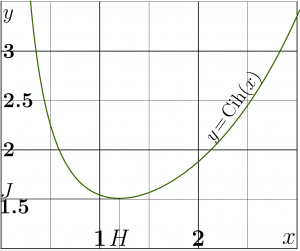
Along the positive part of the real axis, Cih has local minimum, let it be called $H$;

$ \mathrm{Cih}'(H)=0~$ ; $~ ~ H \approx 1.199678640257734$

$ \mathrm{Cih}(H)=J\approx 1.50887956153832$

The expansion of function Cih can be written as follows:

$\displaystyle \mathrm{Cih}(H+t)=

J+\frac{J t^2}{2} +\frac{J t^3}{3H} + \frac{J (8+H^2) t^4}{24~ H^2} + O(t)^5 $ The inversion of the series gives:

$\!\!\!\!\! \displaystyle \mathrm{ArcCih}(J+t)= H+ \sqrt{\frac{2 t}{H}}

+\frac{1}{3H} \left( \frac{2 t}{H}\right) - \frac{3+4/H^2}{72}\left( \frac{2 t}{H}\right)^{3/2} +O(t)^2 $ Function Cip can be represented through Cih as follows:

$ \mathrm{Cip}(z) = - \mathrm{i}~ \mathrm{Cih}(- \mathrm i z)$

giving the expansion of function Cip at $\pm \mathrm i H$.

The inverse of the expansion above can be written as follows:

$\!\!\!\!\! \displaystyle \mathrm{ArcCih}(J+t)= H$ $

+ \left(\frac{2 t}{H}\right)^{1/2} + c_2 \left(\frac{2 t}{H}\right) + c_3 \left(\frac{2 t}{H}\right)^{3/2} + c_4 \left(\frac{2 t}{H}\right)^2 + ...$

$c_2=\frac{1}{3H} \approx 0.27785218653365484$

$c_3 \approx -0.08026758544743313$

$c_4 \approx -0.0631285273509362$

$c_5 \approx ~ 0.012967663071837486$

$c_6 \approx ~ 0.01888997037009226$

This gives the expansion of ArcCip, because

$ \mathrm{ArcCip}(\mathrm i z)=\mathrm i ~ \mathrm{ArcCih}(\mathrm i z)$

Expressions of this section are under testing.

Notations

The notations of this article are not good. Many other similar functions should be described and implemented, anf theu should have similar names. Therefore, the following notations are suggested:

$ \displaystyle \mathrm{sinc}(z)=\frac{\sin(z)}{z}$

$ \displaystyle \mathrm{sihc}(z)=\frac{\sinh(z)}{z}$

$ \displaystyle \mathrm{cosc}(z)=\frac{\cos(z)}{z}=\mathrm{cip}(z)$

$ \displaystyle \mathrm{cohc}(z)=\frac{\cosh(z)}{z}=\mathrm{cih}(z)$

$ \displaystyle \mathrm{BesseLjc}(z)=\frac{\mathrm{BesselJ_0}(z)}{z}$

$ \displaystyle \mathrm{BesseLic}(z)=\frac{\mathrm{BesselI_0}(z)}{z}$

... For the corresponding inverse functions, the following articles should be loaded:
ArcSinc, ArcCosc (which may use some content of this article),
ArcSihc, ArcCohc (which may use some content of this article),
ArcSBesseLj, ArcBesseLi,
ArcSBesseLjc, ArcBesseLic, and so on.
In the case of Bessels, the capital letter L and small letters "j" and "i" are suggested because of the wide distribution of poor fonts, that are designed to cause confusions between characters "|", "l", "I", "|". "l" and "I".

In addition, the non–conflicting names for the extremums of the functions suggested are necessary. Perhaps, these constants should be called
SincMin, SincMv, CoscMin, SCoscMv,
SihcMin, SihcMv, CohcMin, SCohcMv,
BeseLjMin, BesseLjMv, BeseLiMin, BesseLiMv,
BeseLjcMin, BesseLjcMv, BeseLicMin, BesseLicMv.

Also, some generic name is necessary for the article combining all these constants. How about sincation constant?

See also

cos, ArcCos, Sinc, complex map, inverse function