Coshc
Coshc or coshc is elementary function, defined with
- $\displaystyle \mathrm{coshc}(z)=\frac{\cosh(z)}{z}$
where cosh is hyperbolic cosine,
- $\displaystyle \cosh(z)=\cos(\mathrm i z) = \frac{\mathrm e^z+\mathrm e^{-z} }{2}$
The derivative of coshc, id est, cosec', can be expressed with
- $\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \cosh'(z)$ = $\frac{\sinh(z)}{z}-\frac{\cosh(z)}{z^2} $ = $ \mathrm{sinhc}(z) - \frac{\mathrm{coshc}(z)}{z}$
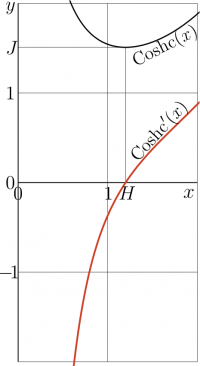
Functions $~y\!=\!\mathrm{coshc}(x)~$ and $~y\!=\!\mathrm{coshc}'(x)~$ are shown in the $x$,$y$ plane.
Coshc is related with the cosc function with the simple relations
- $\displaystyle \mathrm{coshc}(z) = \mathrm i ~ \mathrm{cosc} ( \mathrm i z ) $ $= \mathrm i \frac{\cos(\mathrm i z)}{\mathrm i z}$
- $\displaystyle \mathrm{cosc}(z) = \mathrm i ~ \mathrm{coshc} ( \mathrm i z ) $ $= \mathrm i \frac{\cosh(\mathrm i z)}{\mathrm i z}$
quite analogous to the relation between cos and cosh.
Minimum of $\mathrm{coshc}(x)$ is realized at
- $ x = H\approx 1.199678640257734 ~$ ; $~\mathrm{coshc}'(H)=0$.
- $ J = \mathrm{coshc}(H) \approx 1.50887956153832~$ .
These values are marked in the figure.
Cosch is odd function,
- $\mathrm{coshc}(z)=-\mathrm{coshc}(-z)$
Coshc is holomorphic function with the only singularity, namely, pole at zero. As the real argument increases from zero to infinity, the cosch decreases until its mimumim $J$ at $H$, and again increase, almost exponentially, to infinity.
Asymptotic expansions
At small values of the argument, coshc can be expanded as follows:
- $\displaystyle \mathrm{coshc}(z)=\frac{1}{z}+ \frac{1}{2!} z + \frac{1}{4!}z^3 + \frac{1}{6!}z^5+ ..$
the series converges in the whole compelex plane except zero. This series can be inverted giving the expansion for the inverse function ArcCoshc:
- $ \displaystyle \mathrm{ArcCoshc}(z)=\frac{1}{z}+ \frac{1}{2} \frac{1}{z^3}+ \frac{13}{24} \frac{1}{z^5}+ \frac{541}{720} \frac{1}{z^7}+..$
With Mathematica software one can calculate many coefficients of this expansion. The series seems to converge while $~\left|\frac{1}{z}\right|\!<\!\frac{1}{J}~$, id est, $|z|>J$.
In vicinity of $H$, coshc can be expanded as follows:
- $ \displaystyle \mathrm{coshc}(H+t)=J+\frac{\mathrm{coshc}(H)}{2!} t^2 + \frac{\mathrm{coshc}'(H)}{3!} t^3+..$
which can be simplified to
- $ \displaystyle \mathrm{coshc}(H+t)=J+\frac{J}{2} {t^2} - \frac{J}{3H}{t^3}+ \frac{(8\!+\!H^2)J}{24 H^3}{t^4} -\frac{(10\!+\!H^2)J}{30 H^3}{t^5}+..$
The replacement of $J$ and $H$ to their approximations gives
$ \displaystyle \mathrm{coshc}(H\!+\!t)\approx$ $
1.50887956153832 $ $
+ 0.75443978076916 \,t^2 $ $
- 0.4192454853893647 \,t^3 $ $
+ 0.4123348061601586 \,t^4 $ $
- 0.3332232452918583 \,t^5 $ $
+ 0.2798560879822419 \,t^6 +..$
With Mathematica software one can easy calculate a dozen coefficients of this expansion and evaluate them.
The InverseSeries service allows to express the expansion of the inverse function ArcCoshc:
- $ \displaystyle \mathrm{ArcCoshc}(J+t)=H+\left(\frac{2 t}{J}\right)^{1/2} + \frac{1}{2H} \left(\frac{2 t}{J}\right) -\frac{4+3H^2}{72\,H^2} \left(\frac{2 t}{J}\right)^{3/2} + O(t^2)$
The replacement of $J$ and $H$ to thier approximations gives the approximation
$
\mathrm{ArcCoshc}(J+t)=
1.199678640257734 $ $
+1.1512978931181814\, t^{1/2} $ $
+0.3682894163539221\, t$ $
+0.12249075985507865\, t^{3/2} $ $
-0.11091147932942629\, t^2 $ $
+0.02623011940391186\, t^{5/2}$ $
+O(t^3)$