ArcSinc

Graphic of ArcSinc compared to two its asymptotics and ArcCosc

$u+\mathrm i v=\mathrm{asinc}(x+\mathrm i y)$

ArcSinc is [[inverse function of sinc. ArcSinc is denoted also as $\mathrm{asinc}=\mathrm{sinc}^{-1}$;

$ \displaystyle \mathrm{sinc}(z)= \frac{\sin(z)}{z}~$, $~~\mathrm{sinc}\big(\mathrm{asinc}(z)\big)=z$

As usually, the name of the inverse function is created adding the prefix "Arc" or simply "a".

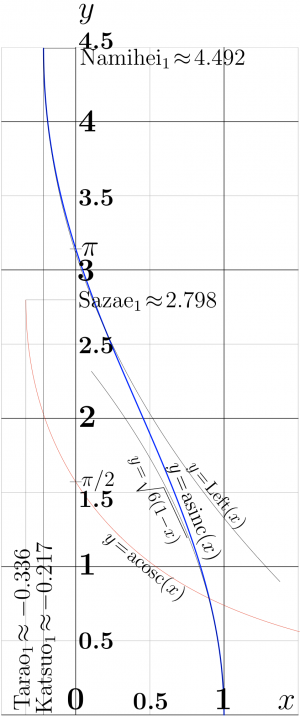
Explicit plot of function ArcSinc is shown in figure at right.

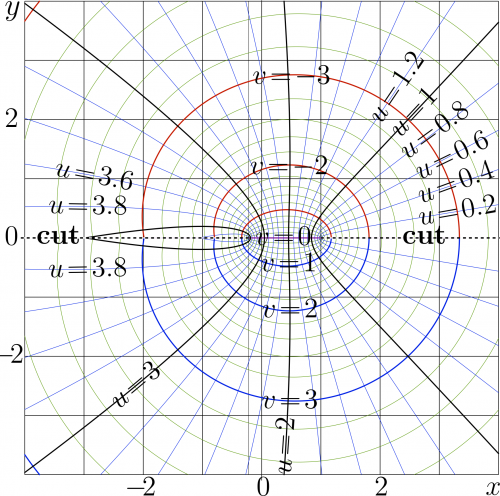
Complex map of ArcSinc is shown below.

Behavior along the real axis

For real values of the argument, $\text{asinc}(x)$ is defined for $\text{Katsuo} \le x\le 1$;

$\mathrm{Katsuo} \approx -0.21723362821122164$.

ArcSinc is monotonously decreasing function. It decrease from value Namihei $\approx 4.493409457909062$ at Katsuo to value 0 at unity.

At the ends of the interval, the derivative is infinite.

Symmetry and holomorphism

ArcSinc is real–holomorphic function,

$ \displaystyle \mathrm{acosc}(z^*)= \mathrm{acosc}(z)^*$

The range of holomorphism of $\mathrm{acosc}(z)$ is the whole complex plane except the cuts $z \ge 1$ and $s \le \mathrm Katsuo \approx -0.21723362821122164$ Sense of the constants Katsuo and Namihei$\approx 4.493409457909062$ is shown in the figure at the top.

Unity and Katsuo are the branch points with square root like singularities.

Expansions

The expansion for ArcSinc follow from those of Sinc. The expansion of sinc at zero can be written as follows:

$ \mathrm{Sinc}(z)= 1-\frac{z^2}{6}+\frac{z^4}{120}-\frac{z^6}{5040}+

..$ The inversion ff this series gives

$\!\!\!\!\!\!\!\! \mathrm{ArcSinc}(1\!-\!t)= \sqrt{6 t} \left(

1-\frac{z^2}{6}+\frac{z^4}{120}-\frac{z^6}{5040}+ ... \right)$ Behavior of the leading term of this expansion is shown in the top figure. It can be used to approximate $\mathrm{ArcSinc}(x)$ at $x\!\approx\!1$.

Constant Namihei is smallest positive solution of equation

$ \mathrm{sinc}'(\mathrm{Namihei})=0$

In vicinity of $~$ Namihei $\approx 4.493409457909062 $ , Sinc can be expanded as follows:

$\!\!\!\!\!\!\!\!\!\displaystyle \mathrm{sinc}(\mathrm{Namihei}\!-\!t)=

\text{Katsuo}$ $\displaystyle -\frac{\text{Katsuo}}{2} t^2 $ $\displaystyle +\frac{\text{Katsuo}} {3 ~ \text{Namihei}} t^3 $ $\displaystyle +\frac{\text{Katsuo} ~

  \left(\text{Namihei}^2\!-\!8\right) }{24 ~
  \text{Namihei}^2} t^4+ ..$

The InverseSeries of this expansion gives

$ \displaystyle \mathrm{asinc}(\mathrm{Katsuo}\!-\!t)= \mathrm{Namihei} - \sqrt{\frac{- 2~ t}{\text{Katsuo}}} $ $\displaystyle

- \frac{2~ \text{Namihei}}{3~ \text{Katsuo}} t +.. $

On the base of this expansion, the approximation

$ \displaystyle \mathrm{Left}(z)= \mathrm{Namihei} - \sqrt{\frac{- 2~ (z\!-\!\text{Katsuo})}{\text{Katsuo}}} $ $\displaystyle

- \frac{2~ \text{Namihei}}{3~ \text{Katsuo}} (z\!-\!\text{Katsuo}) $ is suggested; this function is plotted at the top figure. It approximates ArcSinc in the left hand side of the figure.

Numerical implementation

The efficient complex(fouble) implementation of the ArcSinc is available in the description of figures. It uses the leading terms of the expansions above as the initial approach; then few iterations of the newton method five of order of 15 correct significant figures.

Application

Function ArcSinc appears in the expression for the transversal wavenumber first mode at the guiding of waves between absorbing walls.

The transversal wavenumber of the 0th mode (principal mode) is expressed through function ArcCosc.

Keywords

Sinc, Inverse function, ArcCosc