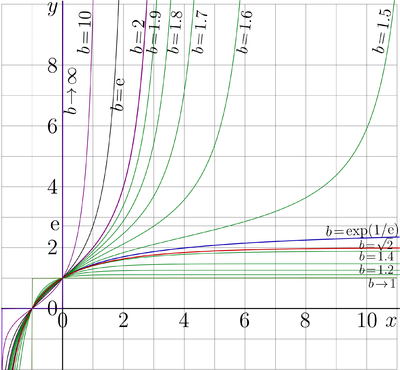
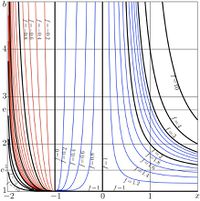
Tetration

$y={\rm tet}_b(x)$ versus $x$ for various $b$

$f={\rm tet}_b(x)$ in the $x,b$ plane shown with levels $f= \rm const$.

Tetration (or Tetrational) ${\rm tet}_b$ to base $b \in \mathbb R$, $b\!>1$
is the $\mathbb C \mapsto \mathbb C$ function, which is solution of equations

${\rm tet}_b(z\!+\!1) = \exp_b\!\big( {\rm tet}_b(z) \big)$

${\rm tet}_b(0) = 1$

such that, at least for $b\!>\!1$, is holomorphic at least in $\{ z \in \mathbb C : \Re(z)\!>\!-2\}$.

Parameter $b$ is called "base", as in the cases of exponential and logarithm. According to the first of equations above, $\mathrm{tet}_b$ is superfunction of exponential to base $b$. Exponential is transfer function of tetration.

For real $b$, it is assumed that ${\rm tet}_b(z^*)={\rm tet}_b(z)^*$, where the asterisk means the complex conjugation. For the case of base $b \!=\! \mathrm e$, the index may be omitted (as in the case of exp and logarithm), id est, ${\rm tet}(z)={\rm tet}_{\rm e}(z)$. The solution is believed to exist and to be unique, although not all mathematicians agree that the proof of the existence and the uniqueness is rigorous.

Case of complex values of $b$ is under investigation; conditions, that make the solution of equations above unique, may have need to be reformulated.

Tetration as superfunction

The tetration is superfunction of the exponential. The tetration can be interpreted as iterated exponential applied to unity. In the language Mathematica, there already exists the special notation for the superfunction, id est, the function Nest. In particular, ${\rm tet}(z)={\rm Nest}[\exp,1,z]$ . Up to year 2011, Nest is implemented only for the integer values of the last argument; the use with any expression, different from an integer constant, causes the error message.

For the beginning of year 2011, the tetration has been analyzed mainly for the real values of base $b \! > \! 1$. The different algorithms are used for the evaluation at $1 \! < \! b \! < \! \exp(1/\rm e)$ , $b \! = \! \exp(1/\rm e)\approx 1.44$ , and for $b \! >\! \exp(1/\rm e)$ . Therefore, one could expect some peculiarity of ${\rm tet}_b(z)$ at $b\!=\!\exp(1/\rm e)$.

On the other hand, the plots of this function look smooth; one might expect that at a fixed value of $z$, ${\rm tet}_b(z)$ is holomorphic (analytic) with respect to $b$, and, in particular, in vicinity of $b \! \approx \! \exp(1/\rm e)$. However, the visual smoothness at the real values of $b$ can substitute neither the investigation of the analytic properties for complex $b$ nor the mathematical proof of holomorphizm.

Behavior at $1\!<\!b\!<\exp(1/{\rm e})$

At $1\!<\!b\!<\exp(1/{\rm e})$, tetration is superfunction constructed with regular iteration at smallest of the real fixed points $L\!=\!L_1$, $L\!=\!L_2$ of $\log_b$. In language Mathematica, the value of the fixed point can be expressed with function ProductLog,

$L_1(b)=-(\mathrm{ProductLog}[- \mathrm{Log}[b]]/\mathrm{Log}[b])$.

The tetration is periodic function; the period

$T=\frac{2\pi \mathrm i} {\ln(L \, \ln(b))} $

is pure imaginary. The cut line $\{x \in \mathbb R: x\le -2\}$ is reproduced at the translations along the imaginary axis.

$\mathrm{tet}_b(x)$ remains real at $x>-2$. It has logarithmic singularity at $x=-2$, and it is [[monotonous function}monotonous]]ly grows at $x>-2$.

The tetration approaches its fixed point $L_1=L_1(b)$ at large values of the real part of its argument (and, in particular, along the real axis).

Evaluation and behavior at $b\!=\! \exp(1/{\rm e})$

For base $b\!=\!\exp(1/{\rm e})\! \approx\! 1.44$, the standard regular iteration should be modified.

In partucular, the "new expansion" is suggested:

$\displaystyle

F(z)=\mathrm e\cdot\left(1-\frac{2}{z}\left(

1+\sum_{m=1}^{M} \frac{P_{m}\big(-\ln(\pm z) \big)}{(3z)^m} +\mathcal{O}\!\left(\frac{|\ln(z)|^{m+1}}{z^{m+1}}\right) \right) \right) $ where

$\displaystyle P_{m}(t)=\sum_{n=0}^{m} ~c_{n,m~}~ t^n$

The substitution of into equation $~ F(z\!+\!1)\!=\!\exp(F(z)/\mathrm e)~$ and the asymptotic analysis with small parameter $|1/z|$ determines the coefficients $c$ in the polynomials above. In particular,

$ \begin{array}{ccc} P_{1}(t)&=&t \\ P_{2}(t)&=&t^{2}+t+1/2 \\ P_{3}(t)&=&t^{3}+\frac{ 5}{ 2}t^{2}+\frac{ 5}{2}t +\frac{ 7}{10} \\ P_{4}(t)&=&t^{4}+\frac{13}{ 3}t^{3}+\frac{ 45}{6}t^{2}+\frac{53}{10}t +\frac{ 67}{60} \\ P_{5}(t)&=&t^{5}+\frac{77}{12}t^{4}+\frac{101}{6}t^{3}+\frac{83}{ 4}t^{2}+\frac{653}{60}t+\frac{2701}{1680} \end{array} $

The evaluation with 9 polynomials $P$ gives an approximation of $\tilde F(z)$ with 15 decimal digits at $\Re(z)\!>\!4$. For small values of $z$, the iterations of formula $F(z)=\ln(F(z\!+\!1))\!~ \mathrm e$ can be used.

The tetration can be approximated as

$\mathrm{tet}_{\exp(1/\mathrm{e})}(z)= F(x_0\!+\!z)$

where $x_0$ is solution of equation $F(x_0)=1$. With the complex double precision, the resulting approximation returns of order of 14 correct decimal digits in the whole complex plane (except the singularities).

The tetration is aperiodic, holomorphic in the range $\mathbb C \backslash \{ x\in \mathbb R : x\!\le\! -2 \}$. A large values of the argument, it approaches the limiting value $\mathrm e$, independently on the direction. In particular, along the real axis, the the function shows the monotonic growth from $-\infty$ at $-2$ to $\mathrm e$ at infinity, passing through points (-1,0) and (0,1).

At any $z$ from the range of definition, In vicinity of $b\!\approx\!\exp(1/\mathrm e)$, tetration $\mathrm{tet}_b(z)$ seems to be continuous function of $b$, although very different agorithms are used for the evaluation in the three cases, $1\!<\!b\!<\!\exp(1/\mathrm e)$, $b=\exp(1/\mathrm e)$, and $b\!>\!\exp(1/\mathrm e)$. The figure below collects the complex maps of tetration to base $b\!=\!1.5$ , left, $b\!=\!\exp(1/\mathrm e)$ , center, and $b\!=\!\sqrt{2}$ , right. $f\!=\! \mathrm{tet}_b(x\!+\!\mathrm i y)$ is shown in the $x,y$ plane with levels $~p\!=\!\Re(f)\!=\! \mathrm{const}~$ and levels $~q\!=\!\Im(f)\!=\! \mathrm{const}~$. The integer values correspond to the thick lines.

Complex maps of $\mathrm{tet}_{b}$ for $b\!=\! 1.5$, $\exp(1/\mathrm e)$ , $\sqrt{2}$; $p\!+\!\mathrm i q=\mathrm{tet}_b(x\!+\!\mathrm i y)$

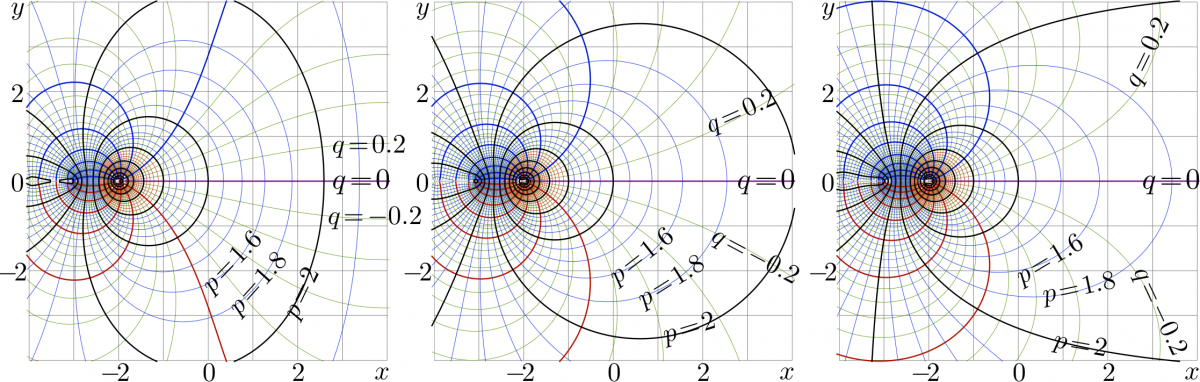
Behavior at $b\!\approx\! \exp(1/{\rm e})$, $z\!\approx\! 0$

If the ${\mathrm{tet}}_b(z)$ is holomorphic in some vicinity of $b\!\approx \! \exp(1/{\rm e})$, $z\!\approx 0$, then it is expandable into the Taylor series

$\displaystyle

{\mathrm {tet}}_b(x)=1+\sum_{n=1}^{N-1} \! \left(\sum_{m=0}^{M-1} \! c_{m,n} \beta^m + O(\beta^M) \right) x^n +{\mathcal O}(x^N) $ where $\beta = b\!-\! \exp(1/\mathrm e)$; the coefficients $c$ of this expansion can be estimated fitting the evaluations of tetration, using the algorithms reported for real base. This leads to the following preliminary estimates:

$

\begin{array}{ccrrrrrr} m&c_{m,0} &c_{m,1} ~ ~ ~& c_{m,2} ~ ~ ~ & c_{m,3} ~ ~ ~ &c_{m,4}~ ~ ~ \\ 0 & 1 & 0.61061 &-0.23171 & 0.09225 &-0.03757\\ 1 & 0 & 0.69521 & 0.41315 &-0.16027& 0.07007 \\ 2 & 0 &-0.57851 & 0.18323 & 0.49162&-0.15216 \\ 3 & 0 & 0.64730 &-0.62933 &-0.51128& 0.51372\\ 4 & 0 &-0.84098 & 1.23261 & 0.42470&-0.97551 \\ 5 & 0 & 1.19090 &-2.12653 &-0.06895& 1.57684 \end{array} $ However, the precision of such evaluation is not so high (perhaps, only two or three decimal digits are significant in the estimates above); for the efficient evaluation of the coefficients of such an expansion, the tetration to the complex base should be analyzed. Such an analysis could be matter for the further research. Any independent confirmation (or correction) of the approximations of the coefficients above should be appreciated.

Behavior at $b\!>\!\exp(1/\mathrm e)\!\approx 1.44$

Tetration is holomorphic in the whole complex plane except part of the real axis $\{ x\in \mathbb R : x\le -2 \}$. As the real part of the argument goes to $-\infty$, the tetration exponentially approaches the fixed point $L$ at the upper halfplane and $L^*$ at the lower halfplane, although has countable set of weak singularities along the cut line $\{ x\in \mathbb R : x\le -2 \}$. As the real part of the argument grows, the tetration shows complicated, fractal-like structures. In the complex map, the lines of zero real part are reproduced at the unity translations along the real axis, but the new and new details appear at each step.

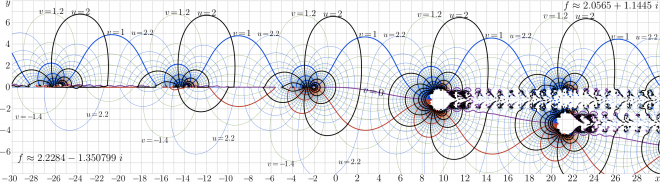
Case $b\!=\! \mathrm{e}$

Complex map of $\mathrm{tet}$

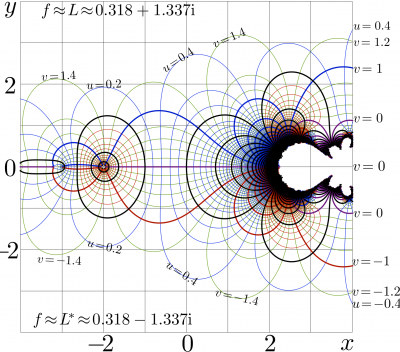
The case of natural tetration refers to base $b\!=\!\mathrm e\! \approx\! 2.71~$; this case is considered in years 2010, 2011 . The fast complex(double) implementation in C++ is suggested.

As in the case of exponential, in the indication of the natural tetration, the subscript can be omitted: $\exp_{\mathrm{e}}=\exp$ and $\mathrm{tet}_{\mathrm{e}}=\mathrm{tet}$.

The figure shows the complex map of natural tetration; the real and the imaginary parts of $f\!=\!\mathrm {tet}(x+\mathrm i y)$ are shown in the $x$,$y$ plane with levels $u\!=\! \Re(f)\!=\! \mathrm {const}$ and $v\!=\! \Im(f)\!=\! \mathrm {const}$.

In the upper half-plane, the tetration approaches the limiting value, which is fixed point $L$ of natural logarithm; $L$ is solution of $L\!=\!\ln(L)$, and $L\!\approx\! 0.318132 + 1.33724 \mathrm i$.

In the lower half-plane, the tetration approaches the conjugated value, id est, $L^*\!\approx\! 0.318132 - 1.33724 \mathrm i$.

Tetration to complex base

$f=\mathrm{tet}_s(x\!+\!\mathrm i y)$ with lines $u\!=\!\Re(f)\!=\!\mathrm{const}$ and $v\!=\!\Im(f)\!=\!\mathrm{const}$

The method with the Cauchi equation can be used also for the complex values of the base. The following properties should be assumed:

$\displaystyle \lim_{y\rightarrow +\infty}$ $\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a)$

$\displaystyle \lim_{y\rightarrow -\infty}$ $\mathrm{tet}_b(x+\mathrm i y)= \mathrm{Filog}(a^*)^*$

where $a=\ln(b)$ and Filog is holomorphic function, $t=\mathrm{filog}(a)$ is solution of equation

$ \log_b(f)=f$

The Filog function can be expressed through the Tania function and through the WrighOmega funciton as follows:

$\displaystyle \mathrm{Filog}(z)= \frac{\mathrm{Tania}\!\big(\ln(z)-1-\mathrm{i}\big)}{-z} = \frac{\mathrm{WrightOmega}\!\big(\ln(z)-\mathrm{i}\big)}{-z}$

Sheldon base

The complex map of $\mathrm{tet}_s$ is shown at figure at right, where $s$ is the Sheldon base,

$\!\!\!\!\!\!\!\! \!\!\!\!\!\!\!\! s=1.52598338517 + 0.0178411853321~{i}$ .

See the special article Tetration to Sheldon base for this case.

The colored plots of various superexponentials for various complex values of base are available at the Tetration Fortum by Sheldon Levenson ; the question wether some of them are tetrations is in discussion.

Fast growth

Along the real axis, the tetration to base $b>\exp(1/\mathrm e)$ shows fast growth; it grows faster than any exponential. Due to such a growth, the tetration could be useful for the numerical representation of huge numbers, that can be stored as $\mathrm {tet}_b(x)$ with moderated values $x$, keeping the stored value of the number distinguishable from $+\infty$. The arithmetics for such "tetrational" variables should be implemented using the properties of the tetration, avoiding the conversion to the conventional floating-point form.

Perhaps, at least in century 21, the tetration satisfies the requirements of the computational mathematics in the rapidly growing functions; if not, the superfunction of tetration, id est, pentation ($\mathrm {pen}_b$) or even higher Ackermann functions are available. For natural base ($b\!=\!\mathrm e\!=\!\exp(1) \approx 2.71$), the pentation $\mathrm{pen}_{\mathrm e}$ can be expressed through the regular iteration, allowing the efficient evaluation while the tetration is already implemented .

Arctetration

Arctetration (ate) is inverse function of tetration; it is Abel function of the exponential. Afctetration $\mathrm {ate}_b$ to base $b$ satisfies the relations

$\mathrm{ate}_b(\mathrm{tet}_b(z))=z$

$\mathrm{tet}_b(\mathrm{ate}_b(z))=z$

at least in some ranges of values of $z$. Also, the arctetration satisfies the Abel equation

$\mathrm{ate}_b(b^z)=\mathrm{ate}_b(z) +1$

Roughly, the arctetration counts, how many times the logarithm should be taken of a value before the value becomes unity.

While the tetration is superfunction of the exponential, the arctetration is the Abel function.

Iterated exponential

The superfunction and the Abel function of the exponential are established; they are tetration "tet" and its inverse function "ate". Then, the iterated exponential can be expressed as follows:

$ \exp_b^c(z)=\mathrm{tet}_b(c+ \mathrm{ate}_b(z))$

In this expression, the number $c$ of iterations ahs no need to be integer; however, at integer values,

$\exp_b^{-2}(z)=\log_b(\log_b(z))$

$\exp_b^{-1}(z)=\log_b(z)$

$\exp_b^{0}(z)= z$

$\exp_b^{1}(z)=\exp_b(z)$

$\exp_b^{2}(z)=\exp_b(b^z)$ ,

at least for values of $z$ in some range in vicinity of the real axis; the arctetration unavoidably has the cut lines in the complex plane.

The realizations of the super-exponentials and the Abel–exponential by Hellmuth Kneser also allow to express the non-integer iterate of the exponential, but the functions he had constructed are not real along the real axis. For the applications to the real numbers, at least for base $b\!>\!1$, the representation of iterated exponential through the tetration and arctetration looks more convenient.

Representation of huge numbers

The tetration and the iterated exponential can be used for the representation of huge numbers. In partucular the number googol which is $10^{100}$ appears to be $\exp_{10}^2(2) = 10^{10^2}$, while the number googolplex appears as $\exp_{10}^3(2)=10^{10^{10^2}}$

Keywords

Arctetration, Natural tetration (to base $b\!=\!e\!\approx \! 2.71$), Tetration to Sheldon base, Superfunction, Transfer equation

More links

http://www.proofwiki.org/wiki/Definition:Tetration
http://en.citizendium.org/wiki/Tetrational
http://en.wikipedia.org/wiki/Tetration
http://math.eretrandre.org/tetrationforum/index.php
http://samlib.ru/k/kuznecow_d_j/ackermann.shtml