Power function
Power function (Степенная функция) is one of the primary elementary functions;
(1) $~ ~ ~ \mathrm{pow}_a(z) = z^a = \exp_z(a) = \exp(a \ln(z))$
where $a$ is parameter; often it is assumed that $a$ is real.
Notations
In C++, $z^a$ can be expressed as $\rm pow(z,a)$. In some realizations, there may be some problems while one of arguments are integer and another one is complex. In some programming languages, including Mathematica, Maple, Matlab aln Latex (in the "math.mode"), the same can be written as z^a.
There is description of the Power function in the Russian version of Wikipedia [1].
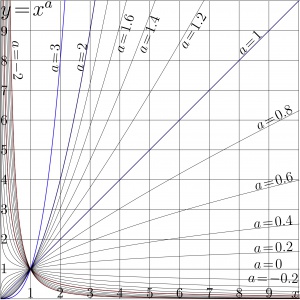
Often, the function is considered with 2 parameters, including the leading coefficient into definition of function [2]. For several real values $a$, the graphic $y=x^a$ is shown in figure 1.
In some cases of integer $a$ the function has specific names.
For $~a\!=\!3~$, the power function $~z^a~$ is cubic function.
For $~a\!=\!2~$, the power function $~z^a~$ is quadratic function.
For $~a\!=\!1~$, the power function $~z^a\!=\!z~$, referring to the identity function.
For $~a\!=\!0~$, the power function $~z^a\!=\!1~$ refers to constant.
For $~a\!=\!-1~$, the power function $~z^a\!=\!1/z~$ and the power function is its own inverse function. For this case, often $~f\!=\! f^{-1}~$ is called "inverse function" (without to indicate, for which function it is "inverse"); using such a term in a context, where the inversion of function take place, may cause confusions.
The confusion may appear also at the use of the superscript after the name of a function to indicate that after to evaluate the function, the power function should be applied to the result. Often this appears dealing with trigonometric functions, one writes, for example, $\sin^a(z)$ instead of $\sin(z)^a~$. In particular, at $~a\!=\!-1~$, this writing may refer also to the ArcSin function. Such a confusion happens at the use of the Mathematica operation TeXForm: expressions $f(z)^n$ are automatically replaced to $f^n(x)$, mimicking the $n$th iteration of function $f$. In TORI, the upper superscript after the function indicates its iteration.
Properties of the power function
the following expressions hold in the wide ranges of values of parameters $a,b,z,p,q,n$:
$ (z)^n/z=z^{n-1}$
$ (z^a)^b = z^(a+b)$
$ (pa)^n=p^n q^n$
However, the use for negative and comlex values of parameters may cause errors. For integer value of power $n$, the expression $(a\!+\!b)^n$ can be simplified as follows
$ (a+b)^1=a+b$
$ (a+b)^2=(a+b)(a+b)=a^2+2ab+b^2$
$ (a+b)^3=(a+b)(a+b)(a+b)=a^3+3a^2b+3ab^2+b^3$
and so on.
Derivative
The derivative of a power function can be derived from the properties of exp and ln:
$\displaystyle {\mathrm{pow}_a}'(z)= \Big(\exp\big( a \ln(z) \big)\Big)^{\prime}_z=\exp\big( a \ln(z) \big) \,a/z=z^a a/z=a z^{a-1}$
Such an expression is valid in wide range of parameters.
Integral
Form the expression for the derivative, the integration of the power function also can be derived:
$\displaystyle \int_x^z t^a \mathrm{d}t = \frac{z^{a+1}}{a\!+\!1}- \frac{x^{a+1}}{a\!+\!1}$
Such an expression is also valid in wide range of parameters, and, especially, while $a\!\ne -1$.
Iterates of power function
The $n$th Iterate of power function can be expressed again through the power function in the following way:
(2) $ ~ ~ ~ {\mathrm {pow}_a}^n(z)=\mathrm{pow}_{b}(z)$
with $b=a^n$. This corresponds to the school–level rules
(3) $ ~ ~ ~ z^p z^q=z^{p+q}$
(4) $ ~ ~ ~ ({z^p})^q=z^{pq}$
however, such a rules should be used carefully, because for come complex values of $p$, $q$ and $z$ the relations (3) and (4) are not valid. Since year 2005, the Mathematica software recognizes this trouble and the Simplify and FullSimplify operations do not use substitutions (3) and (4) automatically before to get some additional information about values of the parameters involved.
The interesting property of iteration of the Power function is that
(5) $ \displaystyle ~ ~ ~ \mathrm{Pow}_{_{(a^n)}}(z) = (\mathrm{Pow}_a)^n(z)$
For this reason, the expression
(7) $ ~ ~ ~ {\mathrm{Pow}_a}^n$
can be interpreted in a way in the left hand side of (5) as well as the expression in the right hand side of (5) in wide range of values of parameters and the argument. (Assuming the same for other functions may lead to confusions.) For $a\!=\!2$, the iterates of quadratic function are shown in Figure 2.
The power function is one of few functions, for which the iterates can be expressed in so simple way. For other function $T$, the $n$th iterate $T^n$ can be expressed through its superfunction $~F~$ and the Abel function $~G=F^{-1}~$,
(8) $~ ~ ~ T^n(z)=F\Big(n+G(z)\Big)$
However, for $T=\mathrm{Pow_a}$, the expression (8) is also valid; the corresponding superfunction $~F~$ and the Abel function $~G~$ are
(9) $~ ~ ~ F(z)=\exp(a^z)$
(10) $~ ~ ~ G(z)=\log_a\Big(\ln(z)\Big)$
Another often confusion is related with the order of operations, while $z^{p^q}$ is interpreted as $(z^p)^q$, while the more usual intepreation is $z^{(p^q)}$. in particular, the Gaussian exponential $\mathrm{gex}(z)=\mathrm e^{-x^2}$ is never interpreted as $(\mathrm e^{-x})^2$. In order to avoid confusions, the use of parenthesis is strongly recommended; also, the representation through exponential and logarithm is appropriate.
Use of the power function
Initially, the power function could be used for short writing of expressions with polynomials with numbers. However, after discovery of exponential and logarithm, by default, $z^a$ is interpreted as $\exp(a \ln(z))$; and are applied for objects of any sets, where operations $\exp$ and $\ln$ are already defined. Even if some of these operations are not yet defined, $z^n$ for natural number $n$ can be considered as just iteration of function "multiplication to \(z\)" applied to unity \(z\) times. In particular, in such a way the power function is interpreted in quantum mechanics; for example, $\hat p^n \psi$ refers to iterative application of operator $\hat p$ to the state $\psi$.
In TORI, the power function is applied mainly to the complex numbers, but the application to the operators of quantum mechanics is expected.