Difference between revisions of "ArcCip"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
[[File:AciplotTa.png|250px|left]] |
[[File:AciplotTa.png|250px|left]] |
||
| − | [[File:CipmapT.png|400px|thumb|[[complex map]] of |
+ | [[File:CipmapT.png|400px|thumb|[[complex map]] of \(u+\mathrm i v=\mathrm{Cip}(x+\mathrm i y)\)]] |
| − | [[File:AcipmapTpng.png|400px|thumb|[[complex map]] of |
+ | [[File:AcipmapTpng.png|400px|thumb|[[complex map]] of \(u+\mathrm i v=\mathrm{ArcCip}(x+\mathrm i y)\)]] |
| − | '''Cip''' |
+ | '''Cip'''\(=\)[[cosc]] is [[elementary function]] constructed through the [[Cos]] function: |
| − | : |
+ | : \(\displaystyle \mathrm {Cip}(z)=\frac{\cos(z)}{z}\) <!-- Complex map of function Cip is shown at right.!--> |
| − | '''ArcCip''' |
+ | '''ArcCip'''\(=\)[[ArcCosc]] is the inverse function, id est, solution of equation |
| − | : |
+ | : \(\displaystyle \mathrm{Cip}(\mathrm{ArcCip}(z))=z\). |
Instead of [[ArcCip]], notation [[ArcCosc]] seems to be better. |
Instead of [[ArcCip]], notation [[ArcCosc]] seems to be better. |
||
| Line 14: | Line 14: | ||
After to load this article, it happened, that inverse function of [[sinc]], id est, |
After to load this article, it happened, that inverse function of [[sinc]], id est, |
||
| − | + | \(\mathrm{sinc}(z)=\sin(z)/x\) |
|
also has application int he atom optics. |
also has application int he atom optics. |
||
The name of function [[sinc]] is already well established. |
The name of function [[sinc]] is already well established. |
||
| Line 23: | Line 23: | ||
==Real argument== |
==Real argument== |
||
| − | Explicit plot |
+ | Explicit plot \(y=\mathrm{ArcCip}(x)\) is shown in left figure for real values of argument \(x\). |
| − | The same figure can be interpreted as [[implicit plot]] |
+ | The same figure can be interpreted as [[implicit plot]] \((\mathrm{Cip}(y),y)\). (In such a way, the figure could be generated without numerical implementation of ArcCip). However, for the application to the channeling of particles by the absorbing walls, the efficient implementation for ArcCip is required, and this implementation is used to plot the [[complex map]]. Complex maps |
| − | : |
+ | : \(f=\mathrm{Cip}(x+\mathrm i y) ~ ~\) and |
| − | : |
+ | : \(f=\mathrm{ArcCip}(x+\mathrm i y)~\) |
are shown in figures at right with |
are shown in figures at right with |
||
| − | lines |
+ | lines \(u\!=\!\Re(f)\!=\!\mathrm{const}\) and |
| − | lines |
+ | lines \(v\!=\!\Im(f)\!=\!\mathrm{const}\) |
==Expansions== |
==Expansions== |
||
==Expansion at large values of the argument== |
==Expansion at large values of the argument== |
||
At small values of argument funcion Cip expands as follows: |
At small values of argument funcion Cip expands as follows: |
||
| − | : |
+ | : \(\displaystyle \mathrm{Cip}(z) = \frac{1}{z} -\frac{z}{2}+\frac{z^3}{24}+\frac{z^5}{720}+...~\), \(~ |z|\!\ll\! 1\) |
This gives the expansion of ArcSip at large values of the argument: |
This gives the expansion of ArcSip at large values of the argument: |
||
| − | : |
+ | : \(\displaystyle \mathrm{ArcCip}(z) = \frac{1}{z} -\frac{1}{2z^3}+\frac{13}{24z^5}-\frac{541}{720z^7}+...\) , \(~ \Re(z)\!>\!0~,~~ |z|\!\gg\! 1\) |
| − | This expansion is used to approximate |
+ | This expansion is used to approximate \(\mathrm{ArcCip}(z)\) for \(\Re(z)\!>\!0\), \(|z|\gg 1\). |
==Expansion at the real branch point== |
==Expansion at the real branch point== |
||
| − | Equation |
+ | Equation \(\mathrm{Cip}'(z)=0\) has several solutions. One of them is \(z=f_0\approx 2.798386045783887\) . |
| − | : |
+ | : \(\mathrm{Cip}'(f_0)\!=\!0~\), |
| − | Denote value of Cip at this point with |
+ | Denote value of Cip at this point with \(x_0\), id est, |
| − | : |
+ | : \( x_0=\mathrm{Cip}(f_0)\approx -0.33650841691839534\) |
Function Cip can be expanded as follows: |
Function Cip can be expanded as follows: |
||
| − | : |
+ | : \(\mathrm{Cip}(f_0+t)=x_0+b_2 t^2+ b_3 t^3 +b_4 t^4 + ...\) |
with |
with |
||
| − | : |
+ | : \(b_2 \approx 0.16825420845919767\) |
| − | : |
+ | : \(b_3 \approx 0.040083630518072705\) |
| − | : |
+ | : \(b_4 \approx 0.00030265472531785555\) |
| − | + | \(x_0\) is branch point ArcCip, and ArcCip can be expanded as follows: |
|
| − | : |
+ | : \(\mathrm{ArcCip}(x_0+t)=f_0 + c_1 \sqrt{z-x_0} +c_2 (z-x_0) + c_3 (z-x_0)^{3/2} + ...\) |
| − | the coefficients |
+ | the coefficients \(b\) can be evaluated inverting the expansion for Cip, that gives |
| − | : |
+ | : \(c_1 \approx 2.437906425896532\) |
| − | : |
+ | : \(c_2 \approx 0.7079542331649882\) |
| − | : |
+ | : \(c_3 \approx 0.5009330133042798\) |
The radios of convergence is determined by the distance to another nearest singularity and is of order of unity. |
The radios of convergence is determined by the distance to another nearest singularity and is of order of unity. |
||
| − | In particular, this expansion can be used for evaluation of ArcCip at small values of argument, |
+ | In particular, this expansion can be used for evaluation of ArcCip at small values of argument, \(|z|\ll 1\). |
==Expansion at the imaginary branch point== |
==Expansion at the imaginary branch point== |
||
| − | Equation |
+ | Equation \(\mathrm{Cip}'(z)=0\) has also pure imaginary solutions |
| − | : |
+ | : \(z=f_0 \approx \, - 1.1996786402577337 ~ \rm i\) |
and |
and |
||
| − | : |
+ | : \(z=f_0^* \approx \! 1.1996786402577337 ~ \rm i\) |
| − | At |
+ | At \(f_0\) function Cip can be expanded as follows: |
| − | : |
+ | : \( \mathrm{Cip}(f_0+t) = z_0 + z_2 t^2 + z_3 t^3 +z_4 t^4 +..\) |
where |
where |
||
| − | : |
+ | : \( z_0 \approx ~ ~ 1.50887956153832 \, \mathrm{i} \) |
| − | : |
+ | : \( z_2 \approx -0.7544397807691602 \, \mathrm{i}\) |
| − | : |
+ | : \( z_3 \approx -0.4192454853893649 \) |
| − | : |
+ | : \( z_4 \approx ~ ~ 0.41233480616015905 \, \mathrm{i}\) |
and |
and |
||
| − | at point |
+ | at point \(z_0\), function ArcCip can be expanded as follows: |
| − | : |
+ | : \(\mathrm{Cip}(z_0+t)= f_0 + f_1 t^{1/2} +f_2 t + f_3 t^{3/2} +..\) |
where |
where |
||
| − | : |
+ | : \( f_0 \approx -1.199678640257734 \, \mathrm{i}\) |
| − | : |
+ | : \( f_1 \approx 0.8140905473896508 + 0.8140905473896508 \mathrm{i}\) |
| − | : |
+ | : \( f_2 \approx -0.4192454853893649 \) |
| − | : |
+ | : \( f_3 \approx 0.08661404692621909 - 0.08661404692621909\, \mathrm{i}\) |
| − | : |
+ | : \( f_4 \approx -0.1109114793294265` \mathrm{i}\) |
| − | In such a way, |
+ | In such a way, \(z_0\) and \(z_0^*\) are branch points of function ArcCip. |
<!-- |
<!-- |
||
For the numeric implementation, it is more convenienr to rewrite the expansion as follows: |
For the numeric implementation, it is more convenienr to rewrite the expansion as follows: |
||
| Line 91: | Line 91: | ||
However, the expansion at imaginary values of argument can be done in more intelligent way. Let |
However, the expansion at imaginary values of argument can be done in more intelligent way. Let |
||
| − | : |
+ | : \( \mathrm{Cih}(z) = \mathrm{i}~ \mathrm{Cip}(\mathrm i z)\) |
then |
then |
||
| − | : |
+ | : \( \mathrm{Cip}(z) = \mathrm{i}~ \mathrm{Cih}(\mathrm i z)\) |
Cih is also real-holomorphic, |
Cih is also real-holomorphic, |
||
| − | : |
+ | : \( \displaystyle \mathrm{Cih}(z) = \frac{\cosh(z)}{z}\) |
| − | Along the positive part of the real axis, Cih has local minimum, let it be called |
+ | Along the positive part of the real axis, Cih has local minimum, let it be called \(H\); |
| − | : |
+ | : \( \mathrm{Cih}'(H)=0~\) ; \(~ ~ H \approx 1.199678640257734\) |
| − | : |
+ | : \( \mathrm{Cih}(H)=J\approx 1.50887956153832\) |
The expansion of function Cih can be written as follows: |
The expansion of function Cih can be written as follows: |
||
| − | : |
+ | :\(\displaystyle \mathrm{Cih}(H+t)= |
| − | J+\frac{J t^2}{2} +\frac{J t^3}{3H} + \frac{J (8+H^2) t^4}{24~ H^2} + O(t)^5 |
+ | J+\frac{J t^2}{2} +\frac{J t^3}{3H} + \frac{J (8+H^2) t^4}{24~ H^2} + O(t)^5 \) |
The inversion of the series gives: |
The inversion of the series gives: |
||
| − | : |
+ | :\(\!\!\!\!\! \displaystyle \mathrm{ArcCih}(J+t)= H+ \sqrt{\frac{2 t}{H}} |
+\frac{1}{3H} \left( \frac{2 t}{H}\right) |
+\frac{1}{3H} \left( \frac{2 t}{H}\right) |
||
- \frac{3+4/H^2}{72}\left( \frac{2 t}{H}\right)^{3/2} |
- \frac{3+4/H^2}{72}\left( \frac{2 t}{H}\right)^{3/2} |
||
| − | +O(t)^2 |
+ | +O(t)^2 \) |
Function Cip can be represented through Cih as follows: |
Function Cip can be represented through Cih as follows: |
||
| − | : |
+ | : \( \mathrm{Cip}(z) = - \mathrm{i}~ \mathrm{Cih}(- \mathrm i z)\) |
| − | giving the expansion of function Cip at |
+ | giving the expansion of function Cip at \(\pm \mathrm i H\). |
The inverse of the expansion above can be written as follows: |
The inverse of the expansion above can be written as follows: |
||
| − | : |
+ | :\(\!\!\!\!\! \displaystyle \mathrm{ArcCih}(J+t)= H\) \( |
+ \left(\frac{2 t}{H}\right)^{1/2} |
+ \left(\frac{2 t}{H}\right)^{1/2} |
||
+ c_2 \left(\frac{2 t}{H}\right) |
+ c_2 \left(\frac{2 t}{H}\right) |
||
+ c_3 \left(\frac{2 t}{H}\right)^{3/2} |
+ c_3 \left(\frac{2 t}{H}\right)^{3/2} |
||
+ c_4 \left(\frac{2 t}{H}\right)^2 |
+ c_4 \left(\frac{2 t}{H}\right)^2 |
||
| − | + ... |
+ | + ...\) |
| − | : |
+ | : \(c_2=\frac{1}{3H} \approx 0.27785218653365484\) |
| − | : |
+ | : \(c_3 \approx -0.08026758544743313\) |
| − | : |
+ | : \(c_4 \approx -0.0631285273509362\) |
| − | : |
+ | : \(c_5 \approx ~ 0.012967663071837486\) |
| − | : |
+ | : \(c_6 \approx ~ 0.01888997037009226\) |
This gives the expansion of ArcCip, because |
This gives the expansion of ArcCip, because |
||
| − | : |
+ | : \( \mathrm{ArcCip}(\mathrm i z)=\mathrm i ~ \mathrm{ArcCih}(\mathrm i z)\) |
Expressions of this section are under testing. |
Expressions of this section are under testing. |
||
| Line 131: | Line 131: | ||
==Notations== |
==Notations== |
||
The notations of this article are not good. Many other similar functions should be described and implemented, anf theu should have similar names. Therefore, the following notations are suggested: |
The notations of this article are not good. Many other similar functions should be described and implemented, anf theu should have similar names. Therefore, the following notations are suggested: |
||
| − | : |
+ | : \( \displaystyle \mathrm{sinc}(z)=\frac{\sin(z)}{z}\) |
| − | : |
+ | : \( \displaystyle \mathrm{sihc}(z)=\frac{\sinh(z)}{z}\) |
| − | : |
+ | : \( \displaystyle \mathrm{cosc}(z)=\frac{\cos(z)}{z}=\mathrm{cip}(z)\) |
| − | : |
+ | : \( \displaystyle \mathrm{cohc}(z)=\frac{\cosh(z)}{z}=\mathrm{cih}(z)\) |
| − | : |
+ | : \( \displaystyle \mathrm{BesseLjc}(z)=\frac{\mathrm{BesselJ_0}(z)}{z}\) |
| − | : |
+ | : \( \displaystyle \mathrm{BesseLic}(z)=\frac{\mathrm{BesselI_0}(z)}{z}\) |
... |
... |
||
For the corresponding inverse functions, the following articles should be loaded:<br> |
For the corresponding inverse functions, the following articles should be loaded:<br> |
||
Latest revision as of 18:25, 30 July 2019


Cip\(=\)cosc is elementary function constructed through the Cos function:
- \(\displaystyle \mathrm {Cip}(z)=\frac{\cos(z)}{z}\)
ArcCip\(=\)ArcCosc is the inverse function, id est, solution of equation
- \(\displaystyle \mathrm{Cip}(\mathrm{ArcCip}(z))=z\).
Instead of ArcCip, notation ArcCosc seems to be better.
Contents
Notations
In analogy with ArcCos, with is denoted also as acos or ACos, the name ACip is also used; ACip=ArcCip.
After to load this article, it happened, that inverse function of sinc, id est, \(\mathrm{sinc}(z)=\sin(z)/x\) also has application int he atom optics. The name of function sinc is already well established. For this reason, the natural chose for the name of function Cip is cosc, and natural name of the inverse function if arccosc=ArcCosc.
The article ArcCosc is suggested to be used instead of this article. The content is mainly the same, but this article is not updated and the ArcCosc is more advanced.
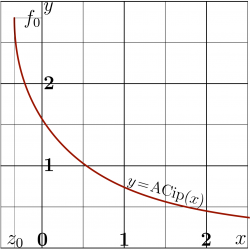
Real argument
Explicit plot \(y=\mathrm{ArcCip}(x)\) is shown in left figure for real values of argument \(x\). The same figure can be interpreted as implicit plot \((\mathrm{Cip}(y),y)\). (In such a way, the figure could be generated without numerical implementation of ArcCip). However, for the application to the channeling of particles by the absorbing walls, the efficient implementation for ArcCip is required, and this implementation is used to plot the complex map. Complex maps
- \(f=\mathrm{Cip}(x+\mathrm i y) ~ ~\) and
- \(f=\mathrm{ArcCip}(x+\mathrm i y)~\)
are shown in figures at right with lines \(u\!=\!\Re(f)\!=\!\mathrm{const}\) and lines \(v\!=\!\Im(f)\!=\!\mathrm{const}\)
Expansions
Expansion at large values of the argument
At small values of argument funcion Cip expands as follows:
- \(\displaystyle \mathrm{Cip}(z) = \frac{1}{z} -\frac{z}{2}+\frac{z^3}{24}+\frac{z^5}{720}+...~\), \(~ |z|\!\ll\! 1\)
This gives the expansion of ArcSip at large values of the argument:
- \(\displaystyle \mathrm{ArcCip}(z) = \frac{1}{z} -\frac{1}{2z^3}+\frac{13}{24z^5}-\frac{541}{720z^7}+...\) , \(~ \Re(z)\!>\!0~,~~ |z|\!\gg\! 1\)
This expansion is used to approximate \(\mathrm{ArcCip}(z)\) for \(\Re(z)\!>\!0\), \(|z|\gg 1\).
Expansion at the real branch point
Equation \(\mathrm{Cip}'(z)=0\) has several solutions. One of them is \(z=f_0\approx 2.798386045783887\) .
- \(\mathrm{Cip}'(f_0)\!=\!0~\),
Denote value of Cip at this point with \(x_0\), id est,
- \( x_0=\mathrm{Cip}(f_0)\approx -0.33650841691839534\)
Function Cip can be expanded as follows:
- \(\mathrm{Cip}(f_0+t)=x_0+b_2 t^2+ b_3 t^3 +b_4 t^4 + ...\)
with
- \(b_2 \approx 0.16825420845919767\)
- \(b_3 \approx 0.040083630518072705\)
- \(b_4 \approx 0.00030265472531785555\)
\(x_0\) is branch point ArcCip, and ArcCip can be expanded as follows:
- \(\mathrm{ArcCip}(x_0+t)=f_0 + c_1 \sqrt{z-x_0} +c_2 (z-x_0) + c_3 (z-x_0)^{3/2} + ...\)
the coefficients \(b\) can be evaluated inverting the expansion for Cip, that gives
- \(c_1 \approx 2.437906425896532\)
- \(c_2 \approx 0.7079542331649882\)
- \(c_3 \approx 0.5009330133042798\)
The radios of convergence is determined by the distance to another nearest singularity and is of order of unity. In particular, this expansion can be used for evaluation of ArcCip at small values of argument, \(|z|\ll 1\).
Expansion at the imaginary branch point
Equation \(\mathrm{Cip}'(z)=0\) has also pure imaginary solutions
- \(z=f_0 \approx \, - 1.1996786402577337 ~ \rm i\)
and
- \(z=f_0^* \approx \! 1.1996786402577337 ~ \rm i\)
At \(f_0\) function Cip can be expanded as follows:
- \( \mathrm{Cip}(f_0+t) = z_0 + z_2 t^2 + z_3 t^3 +z_4 t^4 +..\)
where
- \( z_0 \approx ~ ~ 1.50887956153832 \, \mathrm{i} \)
- \( z_2 \approx -0.7544397807691602 \, \mathrm{i}\)
- \( z_3 \approx -0.4192454853893649 \)
- \( z_4 \approx ~ ~ 0.41233480616015905 \, \mathrm{i}\)
and at point \(z_0\), function ArcCip can be expanded as follows:
- \(\mathrm{Cip}(z_0+t)= f_0 + f_1 t^{1/2} +f_2 t + f_3 t^{3/2} +..\)
where
- \( f_0 \approx -1.199678640257734 \, \mathrm{i}\)
- \( f_1 \approx 0.8140905473896508 + 0.8140905473896508 \mathrm{i}\)
- \( f_2 \approx -0.4192454853893649 \)
- \( f_3 \approx 0.08661404692621909 - 0.08661404692621909\, \mathrm{i}\)
- \( f_4 \approx -0.1109114793294265` \mathrm{i}\)
In such a way, \(z_0\) and \(z_0^*\) are branch points of function ArcCip.
Cih and ArcCih
Warning! The expansions in this section are still under revision!
However, the expansion at imaginary values of argument can be done in more intelligent way. Let
- \( \mathrm{Cih}(z) = \mathrm{i}~ \mathrm{Cip}(\mathrm i z)\)
then
- \( \mathrm{Cip}(z) = \mathrm{i}~ \mathrm{Cih}(\mathrm i z)\)
Cih is also real-holomorphic,
- \( \displaystyle \mathrm{Cih}(z) = \frac{\cosh(z)}{z}\)
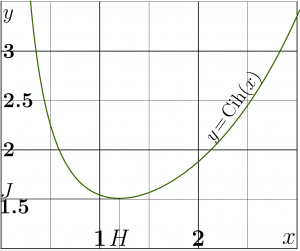
Along the positive part of the real axis, Cih has local minimum, let it be called \(H\);
- \( \mathrm{Cih}'(H)=0~\) ; \(~ ~ H \approx 1.199678640257734\)
- \( \mathrm{Cih}(H)=J\approx 1.50887956153832\)
The expansion of function Cih can be written as follows:
- \(\displaystyle \mathrm{Cih}(H+t)= J+\frac{J t^2}{2} +\frac{J t^3}{3H} + \frac{J (8+H^2) t^4}{24~ H^2} + O(t)^5 \)
The inversion of the series gives:
- \(\!\!\!\!\! \displaystyle \mathrm{ArcCih}(J+t)= H+ \sqrt{\frac{2 t}{H}} +\frac{1}{3H} \left( \frac{2 t}{H}\right) - \frac{3+4/H^2}{72}\left( \frac{2 t}{H}\right)^{3/2} +O(t)^2 \)
Function Cip can be represented through Cih as follows:
- \( \mathrm{Cip}(z) = - \mathrm{i}~ \mathrm{Cih}(- \mathrm i z)\)
giving the expansion of function Cip at \(\pm \mathrm i H\).
The inverse of the expansion above can be written as follows:
- \(\!\!\!\!\! \displaystyle \mathrm{ArcCih}(J+t)= H\) \( + \left(\frac{2 t}{H}\right)^{1/2} + c_2 \left(\frac{2 t}{H}\right) + c_3 \left(\frac{2 t}{H}\right)^{3/2} + c_4 \left(\frac{2 t}{H}\right)^2 + ...\)
- \(c_2=\frac{1}{3H} \approx 0.27785218653365484\)
- \(c_3 \approx -0.08026758544743313\)
- \(c_4 \approx -0.0631285273509362\)
- \(c_5 \approx ~ 0.012967663071837486\)
- \(c_6 \approx ~ 0.01888997037009226\)
This gives the expansion of ArcCip, because
- \( \mathrm{ArcCip}(\mathrm i z)=\mathrm i ~ \mathrm{ArcCih}(\mathrm i z)\)
Expressions of this section are under testing.
Notations
The notations of this article are not good. Many other similar functions should be described and implemented, anf theu should have similar names. Therefore, the following notations are suggested:
- \( \displaystyle \mathrm{sinc}(z)=\frac{\sin(z)}{z}\)
- \( \displaystyle \mathrm{sihc}(z)=\frac{\sinh(z)}{z}\)
- \( \displaystyle \mathrm{cosc}(z)=\frac{\cos(z)}{z}=\mathrm{cip}(z)\)
- \( \displaystyle \mathrm{cohc}(z)=\frac{\cosh(z)}{z}=\mathrm{cih}(z)\)
- \( \displaystyle \mathrm{BesseLjc}(z)=\frac{\mathrm{BesselJ_0}(z)}{z}\)
- \( \displaystyle \mathrm{BesseLic}(z)=\frac{\mathrm{BesselI_0}(z)}{z}\)
...
For the corresponding inverse functions, the following articles should be loaded:
ArcSinc, ArcCosc (which may use some content of this article),
ArcSihc, ArcCohc (which may use some content of this article),
ArcSBesseLj, ArcBesseLi,
ArcSBesseLjc, ArcBesseLic, and so on.
In the case of Bessels, the capital letter L and small letters "j" and "i" are suggested because of the wide distribution of poor fonts, that are designed to cause confusions between characters "|", "l", "I", "|". "l" and "I".
In addition, the non–conflicting names for the extremums of the functions suggested are necessary. Perhaps, these constants should be called
SincMin, SincMv, CoscMin, SCoscMv,
SihcMin, SihcMv, CohcMin, SCohcMv,
BeseLjMin, BesseLjMv, BeseLiMin, BesseLiMv,
BeseLjcMin, BesseLjcMv, BeseLicMin, BesseLicMv.
Also, some generic name is necessary for the article combining all these constants. How about sincation constant?
See also
cos, ArcCos, Sinc, complex map, inverse function