Difference between revisions of "ArcSinc"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
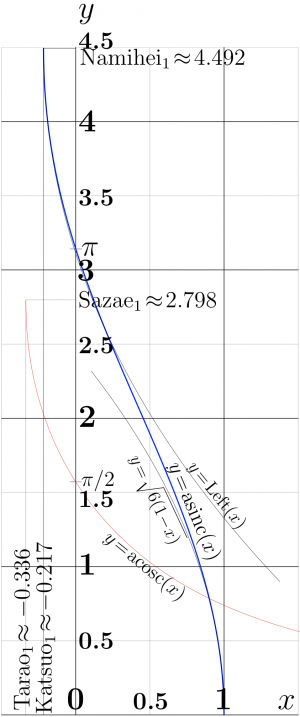
[[File:AsincplotT500.png|300px|right|thumb|Graphic of [[ArcSinc]] compared to two its asymptotics and [[ArcCosc]]]] |
[[File:AsincplotT500.png|300px|right|thumb|Graphic of [[ArcSinc]] compared to two its asymptotics and [[ArcCosc]]]] |
||
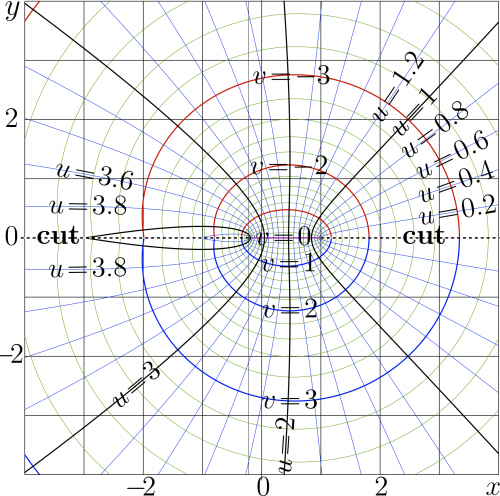
| − | [[File:asincmapT.png|500px|right|thumb| |
+ | [[File:asincmapT.png|500px|right|thumb|\(u+\mathrm i v=\mathrm{asinc}(x+\mathrm i y)\)]] |
| − | '''ArcSinc''' is [[inverse function of [[sinc]]. ArcSinc is denoted also as |
+ | '''ArcSinc''' is [[inverse function of [[sinc]]. ArcSinc is denoted also as \(\mathrm{asinc}=\mathrm{sinc}^{-1}\); |
| − | : |
+ | : \( \displaystyle \mathrm{sinc}(z)= \frac{\sin(z)}{z}~\), \(~~\mathrm{sinc}\big(\mathrm{asinc}(z)\big)=z\) |
As usually, the name of the inverse function is created adding the prefix "Arc" or simply "a". |
As usually, the name of the inverse function is created adding the prefix "Arc" or simply "a". |
||
| Line 10: | Line 10: | ||
==Behavior along the real axis== |
==Behavior along the real axis== |
||
| − | For real values of the argument, |
+ | For real values of the argument, \(\text{asinc}(x)\) is defined for \(\text{Katsuo} \le x\le 1\); |
| − | : |
+ | : \(\mathrm{Katsuo} \approx -0.21723362821122164\). |
| − | ArcSinc is monotonously decreasing function. It decrease from value [[Namihei]] |
+ | ArcSinc is monotonously decreasing function. It decrease from value [[Namihei]] \(\approx 4.493409457909062\) at [[Katsuo]] to value 0 at unity. |
At the ends of the interval, the derivative is infinite. |
At the ends of the interval, the derivative is infinite. |
||
| Line 19: | Line 19: | ||
==Symmetry and holomorphism== |
==Symmetry and holomorphism== |
||
[[ArcSinc]] is real–holomorphic function, |
[[ArcSinc]] is real–holomorphic function, |
||
| − | : |
+ | : \( \displaystyle \mathrm{acosc}(z^*)= \mathrm{acosc}(z)^*\) |
| − | The range of holomorphism of |
+ | The range of holomorphism of \(\mathrm{acosc}(z)\) is the whole complex plane except the cuts |
| − | + | \(z \ge 1\) |
|
and |
and |
||
| − | + | \(s \le \mathrm Katsuo \approx -0.21723362821122164\) |
|
| − | Sense of the constants [[Katsuo]] and [[Namihei]] |
+ | Sense of the constants [[Katsuo]] and [[Namihei]]\(\approx 4.493409457909062\) is shown in the figure at the top. |
Unity and [[Katsuo]] are the branch points with square root like singularities. |
Unity and [[Katsuo]] are the branch points with square root like singularities. |
||
| Line 31: | Line 31: | ||
==Expansions== |
==Expansions== |
||
The expansion for [[ArcSinc]] follow from those of [[Sinc]]. The expansion of [[sinc]] at zero can be written as follows: |
The expansion for [[ArcSinc]] follow from those of [[Sinc]]. The expansion of [[sinc]] at zero can be written as follows: |
||
| − | : |
+ | : \( \mathrm{Sinc}(z)= 1-\frac{z^2}{6}+\frac{z^4}{120}-\frac{z^6}{5040}+ |
<!-- \frac{z^8}{362880}-\frac{z^{10}}{39916800}+!--> |
<!-- \frac{z^8}{362880}-\frac{z^{10}}{39916800}+!--> |
||
| − | .. |
+ | ..\) |
The inversion ff this series gives |
The inversion ff this series gives |
||
| − | : |
+ | : \(\!\!\!\!\!\!\!\! \mathrm{ArcSinc}(1\!-\!t)= \sqrt{6 t} \left( |
1-\frac{z^2}{6}+\frac{z^4}{120}-\frac{z^6}{5040}+ |
1-\frac{z^2}{6}+\frac{z^4}{120}-\frac{z^6}{5040}+ |
||
<!-- \frac{z^8}{362880}-\frac{z^{10}}{39916800}+!--> |
<!-- \frac{z^8}{362880}-\frac{z^{10}}{39916800}+!--> |
||
... |
... |
||
| − | \right) |
+ | \right)\) |
| − | Behavior of the leading term of this expansion is shown in the top figure. It can be used to approximate |
+ | Behavior of the leading term of this expansion is shown in the top figure. It can be used to approximate \(\mathrm{ArcSinc}(x)\) at \(x\!\approx\!1\). |
Constant [[Namihei]] is smallest positive solution of equation |
Constant [[Namihei]] is smallest positive solution of equation |
||
| − | : |
+ | : \( \mathrm{sinc}'(\mathrm{Namihei})=0\) |
| − | In vicinity of |
+ | In vicinity of \(~\) [[Namihei]] \(\approx 4.493409457909062 \) , [[Sinc]] can be expanded as follows: |
| − | : |
+ | : \(\!\!\!\!\!\!\!\!\!\displaystyle \mathrm{sinc}(\mathrm{Namihei}\!-\!t)= |
| − | \text{Katsuo} |
+ | \text{Katsuo}\) \(\displaystyle |
| − | -\frac{\text{Katsuo}}{2} t^2 |
+ | -\frac{\text{Katsuo}}{2} t^2 \) \(\displaystyle |
| − | +\frac{\text{Katsuo}} {3 ~ \text{Namihei}} t^3 |
+ | +\frac{\text{Katsuo}} {3 ~ \text{Namihei}} t^3 \) \(\displaystyle |
+\frac{\text{Katsuo} ~ |
+\frac{\text{Katsuo} ~ |
||
\left(\text{Namihei}^2\!-\!8\right) }{24 ~ |
\left(\text{Namihei}^2\!-\!8\right) }{24 ~ |
||
| − | \text{Namihei}^2} t^4+ .. |
+ | \text{Namihei}^2} t^4+ ..\) |
The [[InverseSeries]] of this expansion gives |
The [[InverseSeries]] of this expansion gives |
||
| − | : |
+ | :\( \displaystyle \mathrm{asinc}(\mathrm{Katsuo}\!-\!t)= \mathrm{Namihei} - \sqrt{\frac{- 2~ t}{\text{Katsuo}}} \) \(\displaystyle |
| − | - \frac{2~ \text{Namihei}}{3~ \text{Katsuo}} t +.. |
+ | - \frac{2~ \text{Namihei}}{3~ \text{Katsuo}} t +.. \) |
On the base of this expansion, the approximation |
On the base of this expansion, the approximation |
||
| − | : |
+ | :\( \displaystyle \mathrm{Left}(z)= \mathrm{Namihei} - \sqrt{\frac{- 2~ (z\!-\!\text{Katsuo})}{\text{Katsuo}}} \) \(\displaystyle |
| − | - \frac{2~ \text{Namihei}}{3~ \text{Katsuo}} (z\!-\!\text{Katsuo}) |
+ | - \frac{2~ \text{Namihei}}{3~ \text{Katsuo}} (z\!-\!\text{Katsuo}) \) |
is suggested; this function is plotted at the top figure. It approximates ArcSinc in the left hand side of the figure. |
is suggested; this function is plotted at the top figure. It approximates ArcSinc in the left hand side of the figure. |
||
Latest revision as of 18:27, 30 July 2019
ArcSinc is [[inverse function of sinc. ArcSinc is denoted also as \(\mathrm{asinc}=\mathrm{sinc}^{-1}\);
- \( \displaystyle \mathrm{sinc}(z)= \frac{\sin(z)}{z}~\), \(~~\mathrm{sinc}\big(\mathrm{asinc}(z)\big)=z\)
As usually, the name of the inverse function is created adding the prefix "Arc" or simply "a".
Explicit plot of function ArcSinc is shown in figure at right.
Complex map of ArcSinc is shown below.
Contents
Behavior along the real axis
For real values of the argument, \(\text{asinc}(x)\) is defined for \(\text{Katsuo} \le x\le 1\);
- \(\mathrm{Katsuo} \approx -0.21723362821122164\).
ArcSinc is monotonously decreasing function. It decrease from value Namihei \(\approx 4.493409457909062\) at Katsuo to value 0 at unity.
At the ends of the interval, the derivative is infinite.
Symmetry and holomorphism
ArcSinc is real–holomorphic function,
- \( \displaystyle \mathrm{acosc}(z^*)= \mathrm{acosc}(z)^*\)
The range of holomorphism of \(\mathrm{acosc}(z)\) is the whole complex plane except the cuts \(z \ge 1\) and \(s \le \mathrm Katsuo \approx -0.21723362821122164\) Sense of the constants Katsuo and Namihei\(\approx 4.493409457909062\) is shown in the figure at the top.
Unity and Katsuo are the branch points with square root like singularities.
Expansions
The expansion for ArcSinc follow from those of Sinc. The expansion of sinc at zero can be written as follows:
- \( \mathrm{Sinc}(z)= 1-\frac{z^2}{6}+\frac{z^4}{120}-\frac{z^6}{5040}+ ..\)
The inversion ff this series gives
- \(\!\!\!\!\!\!\!\! \mathrm{ArcSinc}(1\!-\!t)= \sqrt{6 t} \left( 1-\frac{z^2}{6}+\frac{z^4}{120}-\frac{z^6}{5040}+ ... \right)\)
Behavior of the leading term of this expansion is shown in the top figure. It can be used to approximate \(\mathrm{ArcSinc}(x)\) at \(x\!\approx\!1\).
Constant Namihei is smallest positive solution of equation
- \( \mathrm{sinc}'(\mathrm{Namihei})=0\)
In vicinity of \(~\) Namihei \(\approx 4.493409457909062 \) , Sinc can be expanded as follows:
- \(\!\!\!\!\!\!\!\!\!\displaystyle \mathrm{sinc}(\mathrm{Namihei}\!-\!t)= \text{Katsuo}\) \(\displaystyle -\frac{\text{Katsuo}}{2} t^2 \) \(\displaystyle +\frac{\text{Katsuo}} {3 ~ \text{Namihei}} t^3 \) \(\displaystyle +\frac{\text{Katsuo} ~ \left(\text{Namihei}^2\!-\!8\right) }{24 ~ \text{Namihei}^2} t^4+ ..\)
The InverseSeries of this expansion gives
- \( \displaystyle \mathrm{asinc}(\mathrm{Katsuo}\!-\!t)= \mathrm{Namihei} - \sqrt{\frac{- 2~ t}{\text{Katsuo}}} \) \(\displaystyle - \frac{2~ \text{Namihei}}{3~ \text{Katsuo}} t +.. \)
On the base of this expansion, the approximation
- \( \displaystyle \mathrm{Left}(z)= \mathrm{Namihei} - \sqrt{\frac{- 2~ (z\!-\!\text{Katsuo})}{\text{Katsuo}}} \) \(\displaystyle - \frac{2~ \text{Namihei}}{3~ \text{Katsuo}} (z\!-\!\text{Katsuo}) \)
is suggested; this function is plotted at the top figure. It approximates ArcSinc in the left hand side of the figure.
Numerical implementation
The efficient complex(fouble) implementation of the ArcSinc is available in the description of figures. It uses the leading terms of the expansions above as the initial approach; then few iterations of the newton method five of order of 15 correct significant figures.
Application
Function ArcSinc appears in the expression for the transversal wavenumber first mode at the guiding of waves between absorbing walls.
The transversal wavenumber of the 0th mode (principal mode) is expressed through function ArcCosc.
Keywords
Sinc, Inverse function, ArcCosc