ArcTania
Revision as of 06:58, 1 December 2018 by Maintenance script (talk | contribs)
ArcTania is [[elementary function,
$\mathrm{ArcTania}(z)=z+\ln(z)−1$
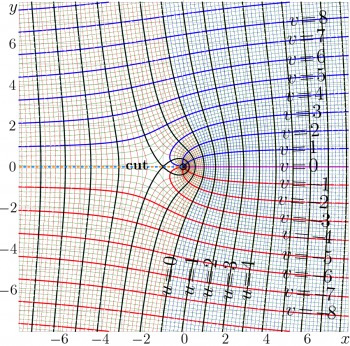
Complex map of ArcTania is shown in figure at right.
ArcTania is important, because its inverse function $\mathrm{Tania}=\mathrm{ArcTania}^{-1}$ , is est, the Tania function, appears in the Laser science as solution of the equation of evolution of intensity of light in the idealised saturable amplifier [1]:
$ \displaystyle \mathrm{Tania}^{\prime}(z)=\frac{\mathrm{Tania}(z)}{1+\mathrm{Tania}(z)} $
References
- ↑
http://link.springer.com/article/10.1007/s10043-013-0058-6
http://mizugadro.mydns.jp/PAPERS/2013or1.pdf
http://mizugadro.mydns.jp/PAPERS/2013or2.pdf D.Kouznetsov. Superfunctions for amplifiers. Optical Review, July 2013, Volume 20, Issue 4, pp 321-326.