Difference between revisions of "BesselJ1"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 2: | Line 2: | ||
[[File:BesselY0J0J1plotT060.png|500px|thumb| |
[[File:BesselY0J0J1plotT060.png|500px|thumb| |
||
[[Explicit plot]] of [[BesselY0]] (red), [[BesselJ1]] (green) and [[BesselJ0]] (blue)]] |
[[Explicit plot]] of [[BesselY0]] (red), [[BesselJ1]] (green) and [[BesselJ0]] (blue)]] |
||
| − | [[File:Besselj1mapT080.png|right|500px|thumb| |
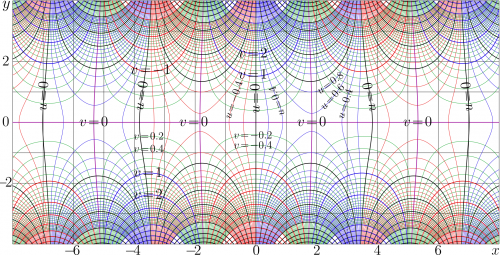
+ | [[File:Besselj1mapT080.png|right|500px|thumb|\( u+\mathrm i v =J_1(x+\mathrm i y)\) ]] |
| − | '''BesselJ1''' or |
+ | '''BesselJ1''' or \(J_1\) is [[Bessel function]] of first order; |
| − | : |
+ | : \(\!\!\!\! \mathrm{BesselJ1}(z)=J_1(z)= \mathrm{BesselJ}[1,z]\) |
| − | Function |
+ | Function \(f=\mathrm{BesselJ1}\) satisfies the [[Bessel equation]] |
<ref> |
<ref> |
||
http://mathworld.wolfram.com/BesselDifferentialEquation.html |
http://mathworld.wolfram.com/BesselDifferentialEquation.html |
||
</ref> |
</ref> |
||
| − | : |
+ | : \( \!\!\!\! |
| − | f''(z)+f'(z)/z + (z^2\!-\!1)f(z) = 0 |
+ | f''(z)+f'(z)/z + (z^2\!-\!1)f(z) = 0\) |
with boundary conditions |
with boundary conditions |
||
| − | : |
+ | : \(f(0) = 0~\) and \(~f'(0)=1/2\) |
| − | The [[complex map]] of |
+ | The [[complex map]] of \(f=J_1(x+\mathrm i y)\) is shown at right in the \(x,y\) plane with |
| − | levels |
+ | levels \(u=\Re(f)=\mathrm {const} ~\) and |
| − | levels |
+ | levels \(v=\Im(f)=\mathrm {const} ~\). |
==Relation to other [[Bessel function]]s== |
==Relation to other [[Bessel function]]s== |
||
| − | : |
+ | : \( J_0'(z)=-J_1(z)\) |
| − | : |
+ | : \(\displaystyle 1-J_0(z)=\int_0^z J_1(t)~\mathrm d t \) |
==Expansions== |
==Expansions== |
||
| − | + | \(J_1\) is [[entire function]], the series |
|
| − | : |
+ | : \(\displaystyle J_1(z) = \frac{z}{2} \sum_{n=0}^\infty |
| − | \frac{(-z^2/4)^n}{(n\!+\!1)~ \mathrm{Factorial}(n)^2} |
+ | \frac{(-z^2/4)^n}{(n\!+\!1)~ \mathrm{Factorial}(n)^2}\) |
| − | converges for any complex |
+ | converges for any complex \(z\) and can be used to plot the complex map at least for \(z<10\) withe the complex(double) arithmetics is available. For large values of \(|z|\), the asymptotic expansion can be used for the precise evaluation: |
| − | : |
+ | : \(\displaystyle |
| − | J_1(z)= |
+ | J_1(z)= \) |
| − | : |
+ | : \(\displaystyle |
\sqrt{\frac{2}{\pi z}} \cos\left(\frac{\pi}{4}+z\right) \left( |
\sqrt{\frac{2}{\pi z}} \cos\left(\frac{\pi}{4}+z\right) \left( |
||
-1 |
-1 |
||
| Line 45: | Line 45: | ||
- \frac{33424574007825}{274877906944 z^{10}} |
- \frac{33424574007825}{274877906944 z^{10}} |
||
+O\left(\frac{1}{z^{12}}\right) \right) |
+O\left(\frac{1}{z^{12}}\right) \right) |
||
| − | + |
+ | +\) |
| − | : |
+ | : \(\displaystyle |
\sqrt{\frac{2}{\pi z}} \sin\left(\frac{\pi}{4}+z\right) |
\sqrt{\frac{2}{\pi z}} \sin\left(\frac{\pi}{4}+z\right) |
||
\left( |
\left( |
||
| Line 57: | Line 57: | ||
+.. |
+.. |
||
\right) |
\right) |
||
| + | \) |
||
| − | $ |
||
| − | This asymptoric expansion is used for the numerical implenentation. However, |
+ | This asymptoric expansion is used for the numerical implenentation. However, \(z\) should not approach the negative part of the real axis. For the case |
| − | + | \(\Re(z)<0\), the symmetry |
|
| − | : |
+ | : \(J_1(z)= - J_1(-z)\) |
is used. |
is used. |
||
| Line 74: | Line 74: | ||
The BesselJ1 is related to the [[BesselJ0]] as follows: |
The BesselJ1 is related to the [[BesselJ0]] as follows: |
||
| − | : |
+ | : \( J_1(z)=-J_0'(z)\) |
==Keywords== |
==Keywords== |
||
Latest revision as of 18:26, 30 July 2019
BesselJ1 or \(J_1\) is Bessel function of first order;
- \(\!\!\!\! \mathrm{BesselJ1}(z)=J_1(z)= \mathrm{BesselJ}[1,z]\)
Function \(f=\mathrm{BesselJ1}\) satisfies the Bessel equation [1]
- \( \!\!\!\! f''(z)+f'(z)/z + (z^2\!-\!1)f(z) = 0\)
with boundary conditions
- \(f(0) = 0~\) and \(~f'(0)=1/2\)
The complex map of \(f=J_1(x+\mathrm i y)\) is shown at right in the \(x,y\) plane with levels \(u=\Re(f)=\mathrm {const} ~\) and levels \(v=\Im(f)=\mathrm {const} ~\).
Contents
Relation to other Bessel functions
- \( J_0'(z)=-J_1(z)\)
- \(\displaystyle 1-J_0(z)=\int_0^z J_1(t)~\mathrm d t \)
Expansions
\(J_1\) is entire function, the series
- \(\displaystyle J_1(z) = \frac{z}{2} \sum_{n=0}^\infty \frac{(-z^2/4)^n}{(n\!+\!1)~ \mathrm{Factorial}(n)^2}\)
converges for any complex \(z\) and can be used to plot the complex map at least for \(z<10\) withe the complex(double) arithmetics is available. For large values of \(|z|\), the asymptotic expansion can be used for the precise evaluation:
- \(\displaystyle J_1(z)= \)
- \(\displaystyle \sqrt{\frac{2}{\pi z}} \cos\left(\frac{\pi}{4}+z\right) \left( -1 - \frac{15}{128 z^2} +\frac{4725}{32768 z^4} - \frac{2837835}{4194304 z^6} + \frac{14783093325}{ 2147483648 z^8} - \frac{33424574007825}{274877906944 z^{10}} +O\left(\frac{1}{z^{12}}\right) \right) +\)
- \(\displaystyle \sqrt{\frac{2}{\pi z}} \sin\left(\frac{\pi}{4}+z\right) \left( \frac{3}{8 z} - \frac{105}{1024 z^3} + \frac{72765}{262144 z^5} - \frac{66891825}{33554432 z^7} + \frac{468131288625}{17179869184 z^9} - \frac{1327867167401775}{2199023255552 z^{11}} +.. \right) \)
This asymptoric expansion is used for the numerical implenentation. However, \(z\) should not approach the negative part of the real axis. For the case \(\Re(z)<0\), the symmetry
- \(J_1(z)= - J_1(-z)\)
is used.
Mathematica allows to calculate a dozen of term of this expansion; they can be extracted also from the complex(double) implementation Besselj1.cin.
Evaluation at real argument
At real values of the argument, the GNU library [2] can be used for the evaluation.
The BesselJ1 is related to the BesselJ0 as follows:
- \( J_1(z)=-J_0'(z)\)
Keywords
BesselJ0, Bessel function, Special function, Entire function, Cylindric function
References
http://mathworld.wolfram.com/BesselFunctionoftheFirstKind.html