Morias
morias is asymptotic approximation of function mori at large values of its argument.
$\mathrm{mori}(z)=\displaystyle \frac{ J_0 (L_1 z)}{1-z^2}$
where $L_1\approx 2.4$ is first zero of the Bessel function, $J_0(L_1)\!=\!0~$.
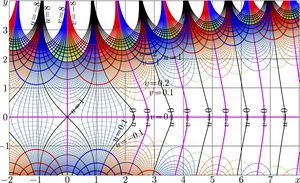
Complex map of function mori is shown in the top figure with
$u\!+\!\mathrm i v=\mathrm{mori}(x\!+\!\mathrm i y)$
For integer $m>0$ and $|z|\gg 1$, function mori$(z)$ can be approximated with
$\displaystyle \mathrm{mori}(z) \approx \mathrm{morias}_m(z) $ $\displaystyle= - \sqrt{\frac{2}{\pi L_1}} z^{-5/2} \, G_m(z^2)\, \cos\left( - \frac{\pi}{4} + L_1 z\, F_m(z^2) \right) $
where
$G_m(x) = \sum_{n=0}^{m} g_n x^{-n}$
$F_m(x) = \sum_{n=0}^{m} f_n x^{-n}$
The coefficients $f$ and $g$ can be calculated from the asymptotic expansion of the Hankel function;
$\begin{array}{l} f_0=1\\ f_1=- 0.021614383628830615865\\ f_2=0.0019465899152260872595\\ f_3=-0.0010834984344719114778\\ f_4=0.001464410164512283719\\ f_5=-0.003628876399615993660\\ f_6=0.01431760830195380729\\ f_7=-0.0824438982874790057\\ f_8=0.652747801052423657\\ f_9=-6.80376838070624330\\ f_{10}=90.322658904953727\\ f_{11}=-1487.942880868968812\\ f_{12}=29785.50901270392374\\ \end{array}$ $~$ $\begin{array}{l} g_0=1 \\ g_1=0.989192808185584692068 \\ g_2=0.99228788615079417081 \\ g_3= 0.989481317221334367489\\ g_4= 0.994709980602617872387\\ g_5= 0.97818700495778240956\\ g_6=1.0575251177784290263\\ g_7= 0.5188843197279991625\\ g_8=5.432808917007474985\\ g_9=-52.5640507009104629\\ g_{10}=807.429675670594971\\ g_{11}= -14844.4023379433794\\ g_{12}=328204.367306340176 \end{array}$
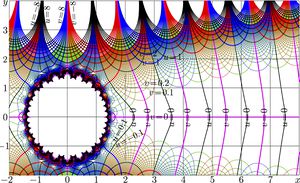
For $m\!=\!11$, the complex map of function $\mathrm{morias}_m$ is shown in figure at right. At this value of $m$, the last line in the table above is not used, as the following increase of number of terms, taken into account, does not improve the precision of approximation with the complex double arithmetics in the examples and numerical tests.
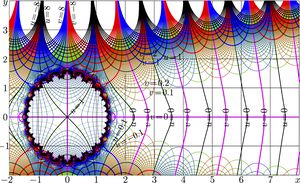
Overlapping of the first two maps is shown in the third image at right.
Function $\mathrm{morias}_{11}(z)$ approximates $\mathrm{mori}(z)$ at $|z|\!>\!2$, and, for $|z|\!>\!4$, it provides the precise approximation; the error of this approximation is small compared to the rounding error for the complex double variables.
Application
Function morias seems to be useful for the efficient evaluation of function naga that refers of the loss of the pinhole waveguide. However, for the contour integral, morias of the complex argument should be implemented.
For the numerical testing of the asymptotic formulas of the complex argument, it is neserably to have function implemented in a "dingle piece". Then, for the commercial implementation as a built-in function of some language or software, the appropriate combination of morias and expansion of function mori for small and moderate values of the argument can be arranged.
References
Keywords
Bessel function, BesselJ0, kori, Morinaga function, nori, Pinhole waveguide