Tetration to Sheldon base
Tetration to Sheldon base refers to the specific case of tetration to the complex base $b=s$, where
- $\!\!\!\!\!\!\!\! \!\!\!\!\!\!\!\! s=1.52598338517 + 0.0178411853321~ {i}$.
is the Sheldon number. In such a way, it is holomorphic function $\mathrm{tet}_s$.
Yet, no specific definition for the Sheldon number is available; the only observation by Sheldon Levenstein that the tetration to such a base is very difficult to evaluate [1] with his algorithm of "merging of solution" [2].
Following the general ideology of TORI, the solutions that are believed not to exist (or to be extremely difficult to evaluate) are of special interest. For this reason, tetration to the Sheldon base is described in this article.
Fixed points of logs and properties of tets
According to the general expectations about tetration $\mathrm{tet}_s$, it satisfies the transfer equation:
- $\!\!\!\!\!\!\!\! (1) \displaystyle ~ ~ ~ \exp(a~ \mathrm{tet_s}(z)) = \mathrm{tet}_s(z\!+\!1)$
where $a=\ln(b)\approx 0.4227073870410604 + 0.0116910660021443~ i$ with the additional condition
- $\!\!\!\!\!\!\!\! (2) \displaystyle ~ ~ ~ \mathrm{tet_s}(0)=1$
and the asimptitic behavior determined with function Filog :
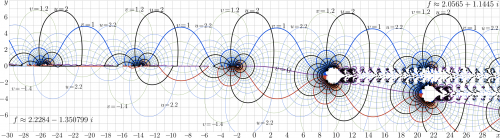
- $\!\!\!\!\!\!\!\! (3) \displaystyle ~ ~ ~ \lim_{y \rightarrow +\infty} \mathrm{tet_s}(x+\mathrm i y)=L_1=\mathrm{Filog}(a)\approx 2.0565398441043761 +1.1445267140098765~ i$
- $\!\!\!\!\!\!\!\! (4) \displaystyle ~ ~ ~ \lim_{y \rightarrow -\infty} \mathrm{tet_s}(x+\mathrm i y)=L_2=\mathrm{Filog}(a^*)^*\approx 2.2284359658711805 -1.3507994961102865~ i$
In addition, $\mathrm{tet}_s(z)$ is supposed to be holomorphic at least for $z>-2$, and also in the left hand side of the complex half-line, except some facility of the negative part of the real axis $z<-2$; the tetration should have the cutline there.
In the upper half-plane, the tetration should behave as $L_1+\exp(k_1 (z-z_1)) + O(\exp(2 k_1 (z-z_1))$;
In the lower half-plane, the tetration should behave as $L_2+\exp(k_2 (z-z_1)) + O(\exp(2 k_2 (z-z_2))$;
for some complex constants $z_1$ and $z_2$, at
$~k_1 =\ln(L_1 a) ~$ and
$~k_2 =\ln(L_2 a) ~$.
For the Sheldon base, the increments $k_1$ and $k_2$ are evaluated as
- $k_1 =\ln(L_1 a) \approx -0.0047589243931785 + 0.5354935770338939~ i$
- $k_2 =\ln(L_2 a) \approx 0.0970758595007548 - 0.517289596155984~i$
The quasiperiod in the upper half-plane
- $T_1=2 \pi/k_1 \approx -0.1042667514229599~i + 11.7325200133916496~ $
and that in the lower half-plane is
- $T_2=2 \pi/k_2 \approx -2.2018723603861230~i + 11.7331504449085493~ $
These quasi-periods are used to arrange the labels at the complex map of the tetration with the multiput command; in the upper half-plane the increment is $T_1$, and in the lower half-plane, it is $T_2$.
The properties above give the simple and efficient way of the precise evaluation of $\mathrm{tet}_s$ through the Cauchi integral equation [3].
References
- ↑ Sheldon Levenstein. Tetration for e^(1/e) branch point. Sun, 19 Feb 2012 06:20:26 -0600. .. I don't have a working generic algorithm for any generic complex base, especially one near the Shell Thron boundary. For example, consider the superfunction developed from the attracting fixed point, where sexp_b(1), for an arbitrary complex base b inside the Shell Thron boundary, For a specific case, consider b=1.52598338517 + 0.0178411853321~ i. This imaginary component of this base is about 10% bigger than the nearest base that is only the Shell Thron boundary.
- ↑ http://math.eretrandre.org/tetrationforum/showthread.php?tid=729 Sheldon Levenson. Complex base tetration program. Tetration and Related Topics, 2012 March 1.
- ↑ http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html D.Kouznetsov. (2009). Solutions of $F(z+1)=\exp(F(z))$ in the complex plane.. Mathematics of Computation, 78: 1647-1670.
Keywords
Tetration, superfunction, transfer equation, Sheldon Levenstein