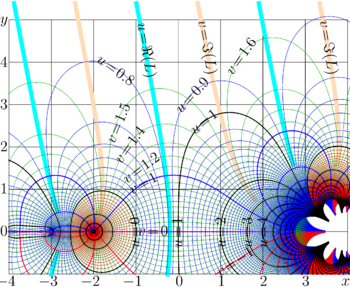
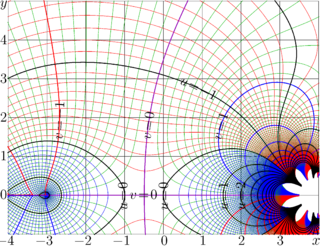
Tetration to base 2
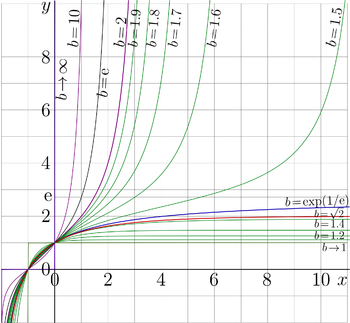 Fig.1. \(y=\mathrm{tet}_b(x) \) for vaious \(b\). See
[1], Fig.17.1.
Fig.1. \(y=\mathrm{tet}_b(x) \) for vaious \(b\). See
[1], Fig.17.1.
Tetration to base 2 (Tet2 or \(\mathrm {tet}_2\) ) is special case of Tetration \(\mathrm {tet}_b\) while the base \( b\!=\!2\).
For real values of argument, tetration to base 2 is compared to tetrations to other bases in Fig.1.
Complex map of tetration to base 2 is shown in Fig.2.
Equations
Tetration to base 2 appears as superfunction of exponential to base 2.
Function \(~ T(z)=\exp_2(z)=\exp(\ln(2)z)=2^z \)
is considered as Transfer function.
The Superfunction \(F\) is solution of the Transfer equation
\( F(z\!+\!1)=T(F(z)) \)
The solution \(F\) is called Tetration to base 2 and denoted \(F=\mathrm{tet}_2\), if it satisfies condition
\(F(0)=1\)
and additional conditions:
\(F(z) \) is real holomorphic in the whole complex \(z\) plane except halfline \(z\le -2\).
\( F(z)\) approaches the fixed point \(L\) of logarithm to base 2 in the upper half plane and \(L^*\) in the lower half plane. This fixed point can be espressed with function Filog:
\( L=\) Filog\((\ln(2)) \) \(\approx 0.8246785461420740 + 1.5674321238496474 \, \mathrm i \)
This requirement can be written as follows:
\( \displaystyle \lim_{y\rightarrow + \infty} F(x\!+\!\mathrm i y)=L \)
\( \displaystyle \lim_{y\rightarrow - \infty} F(x\!+\!\mathrm i y)=L^* \)
\( \displaystyle \lim_{x\rightarrow -\infty} F(x\!+\!\mathrm i y)=L \) for \(y\!>\!0\)
\( \displaystyle \lim_{x\rightarrow -\infty} F(x\!+\!\mathrm i y)=L^* \) for \(y\!<\!0\)
The conditions above are a little bit redundant, some of them follow from other. Up to year 2020, it is not yet established, which of these conditions should be kept in the definition of tetration, and which of them should be deduced as theorems.
Properties
At integer values of argument, beginning with \(-1\), tetration to base 2 has integer values; in particular,
\(\mathrm{tet}_2(-1)=0\)
\(\mathrm{tet}_2(0)=1\)
\(\mathrm{tet}_2(1)=2\)
\(\mathrm{tet}_2(2)=4\)
\(\mathrm{tet}_2(3)=16\)
\(\mathrm{tet}_2(4)=2^{16}=65536\)
\(\mathrm{tet}_2(5)=2^{65536}\) is already too large for the decimal representation
At \(z =-2\), function \(\mathrm{tet}_2\) has logarithmic singularity and branch point, but function
\( \tau(z)= \mathrm{tet}_2(z)-\log_2(2\!+\!z) \)
looks smooth at this point; the cut begins only with \(z=-3\), and goes to minus infinity. Complex map of function \(\tau\) is shown in Fig.3.
In the upper halfplane, tetration to base 2 approaches the displaced Kneser superexponential Tek\(_2\),
\( \mathrm{tet}_2 \approx\) Tek\(_2(z-Z_\mathrm k) \) , \( \Im(z)\rightarrow \infty \)
For base \(b=2\), the Kneser parameter
\(Z_{\mathrm k} \approx 1.23806941407137 + 1.24816132484493 \,\mathrm i \)
Implementation
The primary implementation of Tetration to base 2 is based on the Cauchi integral along the special rectangular contour [2]
The secondary implementation (faster and more precise) uses the Kneser expansion for large values of imaginary part of the argument and two Taylor expansions for moderate values of the imaginary pat of the argument, in analogy with implementation of the natural tetration [3]
The primitive complex double routine in C++ is loaded as Tet2.cin.
Also, the imlementation in Mathematica, based on the modified Kneser expansion is described by William Paulsen and Samuel Cowgill for various base \(b\) (not only for \(b\!=\!2\) [4]. The online evaluator is arranged [5]
References
- ↑
https://www.morebooks.de/store/gb/book/superfunctions/isbn/978-620-2-67286-3
https://mizugadro.mydns.jp/BOOK/466.pdf Dmitrii Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
https://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. LAP, 2014. ISBN-13: 978-3-659-56202-0 (In Russian) - ↑ https://www.jstor.org/stable/40234677?seq=1 D.Kouznetsov. Solution of F(z+1) = exp(F(z)) in Complex z-Plane Mathematics of Computation, Vol. 78, No. 267 (Jul., 2009), pp. 1647-1670
- ↑ https://mizugadro.mydns.jp/PAPERS/2010vladie.pdf D.Kouznetsov. Tetration as special function. (In Rusian) Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45. Russian original: http://www.vmj.ru/articles/2010_2_4.pdf
- ↑ https://link.springer.com/article/10.1007/s10444-017-9524-1 William Paulsen & Samuel Cowgill. Solving F(z + 1) = b F(z) in the complex plane. Advances in Computational Mathematics volume 43, pages1261–1282(2017). 07 March 2017
- ↑ http://myweb.astate.edu/wpaulsen/tetcalc/tetcalc.html First, select the base b from the menu. This produces a graph below. Then enter the real and complex parts of z, and press Compute. The tetration tetb(z) will be computed to about 20 places. (observed in year 2020)