Amos
Amos (or amos) is special function, defined through function Lof:
\(\mathrm{Amos}(z)=\) \(\displaystyle \pi^{-1/4} \exp\!\left(\frac{1}{2}\mathrm{Lof}(z)-\mathrm{Lof}\Big(\frac{z}{2}\Big)-\frac{\ln(2)}{2} z \right)\)
For moderate values of phase of \(z\), Lof\((z)\!=\)ln\((z!)\!=\)ln\(\big(\)Factorial\((z)\big)\), and the representation through the Factorial is valid:
\(\mathrm{Amos}(z)=\) \( \displaystyle \frac{2^{-z/2}\,\sqrt{z!}} {\pi^{1/4}\, (z/2)!}=\) \( %\displaystyle \frac{2^{-z/2}} {\pi^{1/4}} \, \)Factorial\((z/2)^{1/2}/\)Factorial\((z/2)\)
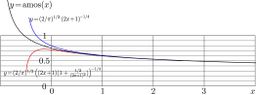
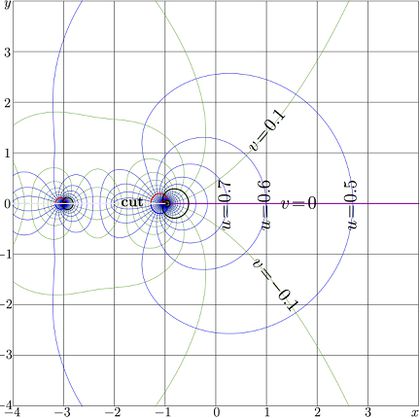
Explicit plot of function Amos of real argument is shown in figure at right wtth black curve. For comparison, the two its asymptotic approximations are also plotted with coloured curves. Below the complex map of function Amos is shown with lines of its content real part and linens of constant imaginary part.
Notations and etymology
Name Amos means Amplitude of of oscillations of the Oscillator function at zero; for non-negative even integer values of the argument, it represents the amplitude of the oscillator function.
The need for the asymptotic analysis, necessary for summation of the asymptotic series, the extension to the complex plane is essential. For this reason, the special name is required for the holomorphic extension of the simple expression above thrush the Factorial. Namely this extension is denoted with name amos or Amos, as the default support of mediawiki (that provides TORI) automatically capitalises the first letter of the name of the article. The complex map of function Amos is shown in figure at right with lines \(u\!+\!\mathrm i v=\mathrm{Amos}(x\!+\!\mathrm i y)\) in the \(x\), \(y\) plane.
Expansions
Expansion at zero
\(\mathrm{amos}(z)\approx\) \(\displaystyle \pi^{-1/4} \left( 1+\frac{\ln(2)}{2} x + \Big(\frac{\ln(2)^2}{8}-\frac{\pi^2}{48} \Big) x^2 + O\big(x^3\big) \right)\)
or, more general,
\(\mathrm{amos}(z)\approx\) \(\displaystyle \sum_{n=0}^{M-1} s_n x^n+O(x^M)\)
where
\(s_0=1\)
\(s_1\approx\! - 0.34657359027997264\)
\(s_2 \approx~~ 0.2656733850958034\)
\(s_3 \approx\! -0.22845646464323024\)
\(s_4 \approx~~ 0.20454315840393944\)
\(s_5 \approx\! -0.18695286574761075\)
\(s_6 \approx~~ 0.17315355476832262\)
\(s_7 \approx\! -0.16192641258125995\)
\(s_8 \approx~~ 0.15256678414566321\)
\(s_9 \approx\! -0.14461945918945732\)
Advanced expansion at zero
\(\mathrm{amos}(z)\approx\) \(\displaystyle \frac{\pi^{-1/4}} {\sqrt{1+z}} \left(1 + \frac{1\!-\! \ln(2)} {2} x + \frac{\pi^2\!-\!6\!+\!6\ln(2)\!-\!12 \ln(2)^2}{48} x^2 + O\big(x^3\big) \right)\)
\(\mathrm{amos}(z)\approx\) \(\displaystyle \frac{\pi^{-1/4}} {\sqrt{1+z}} \left( \sum_{m=1}^{M-1} t_m x^m + O\big(x^M\big) \right) \)
where
\(t_0=~~ 1.\)
\(t_1\approx~~ 0.15342640972002736\)
\(t_2\approx- 0.03261341004418285 \)
\(t_3\approx~~ 0.010201926689668017 \)
\(t_4\approx- 0.0036175964471494145 \)
\(t_5\approx~~ 0.0013621389735619315\)
\(t_6\approx 0.0005316026606999278 \)
\(t_7\approx~~ 0.00021275515235195884\)
\(t_8\approx- 0.00008685289788848534 \)
\(t_9\approx~~ 0.000036057089495484805\)
\(t_{10}\approx\! - 0.000015193001122005512\)
Asymptotic behaviour at infinity
At large values of the argument, namely, \(\arg[z]=\mathrm{const}<\pi\), \(|z|\rightarrow \infty\), function Amos can be represented with its asymptotic series
\(\mathrm{amos}(z)\approx\) \(\displaystyle \frac{(2/\pi)^{1/2}} {\displaystyle \left( (2z\!+\!1) \left(\sum_{m=0}^{M-1} c_m\, (2z\!+\!1)^{-2m} + O(2z\!+\!1)^{-2M} \right)\right)^{1/4}}\)
with
\(c_0=1\)
\(c_1=1/2\)
\(c_2=-9/8\)
\(c_3=153/16\)
\(c_4=-21429/128\)
For real values of argument, the two approximations by this asymptotic with \(M\!=\!0\) and \(M\!=\!1\) are shown with coloured lights in the explicit plot at the top. With Mathematica software, one can easy calculate a dozen of coefficients \(c\). With \(\!=\!13\), the asymptotic approximation provides of order of 15 correct decimal digits for \(\Re(z)\!>\!10\) (or \(|\Im(x)|>11\)); this is floe to the best precision available for the complex double variables. The following increase of the number of terms in the asymptotic expansion does not allow to extend the range of approximation with this precision.
The asymptotic representation fails in vicinity of the negative part of the real axis, where function Amos has cut line.
The effective expansion parameter \((2z\!+\!1)^{-1}\) bas physical sense of the inverse of energy of the \(z\)th oscillator mode. Roughly, the amplitude of its oscillation decays as power "minus quarter" of this energy.
Applications
For non–negative integer values of the argument, Amos appears as amplitude of oscillations of the \(n\)th oscillator function \(\psi_n\) at zero; in particiular, for non-nevarive integer \(n\),
\(\psi_n(0)= \cos\!\left(\frac{\pi}{2}n\right) \mathrm{Amos}(n)\)
where oscillator function
\(\psi_n(x)= N_n^{-1/2}\, H_n(x)\, \exp(-x^2/2)\)
\(H_n\!=\)HermiteH\(_n\) is the \(nth\) Hermite polynomial,
and \(N_n\) is the normalisation factor,
\(N_n=\int_{-\infty}^{\infty} H_n(x)^2 \exp(-x^2)\,\mathrm{d}x\) \(~= 2^n\, n!\, \sqrt{\pi}\)
This quantity is related also to the Hermite number; for real \(n\ge -1/2\),
\(H_n=H_n(0)\) \(= \cos\left(\frac{\pi}{2}n\right)\displaystyle \frac{n!}{(n/2)!} \)
Also, for integer \(n\), \(H_n=H_n(0)\) \(= 2^n \sqrt{\pi}\,/\,\mathrm{Gamma}(1/2(1-n)))=\) \( 2^n \sqrt{\pi}/\)Factorial\(\big(\!-(1\!+\!n)/2\big)\)
All these expressions may have sense also for complex \(n\), but they may have different range of holomorphism.
References
http://mathworld.wolfram.com/HermiteNumber.html
Weisstein, Eric W. "Hermite Number." From MathWorld--A Wolfram Web Resource.
Keywords
Factorial, Gauss Hermite, Harmonic oscillator, Hermite number, Hermite polynomial, HermiteH, Lof, Oscillator function Special function