Morinaga function

Morinaga function \(\displaystyle \mathrm{mori}(x)=\frac{J_0(L_1\, x)} {1\!-\!x^2}~\), where \(J_0\) is Bessel function and \(L_1\approx 2.4\) is its first zero.
Morinaga function appears at the consideration of guiding of the paraxial wave packet by the set of pinholes. Plot of the Morinaga function is shown in the top figure. For comparison, the Bessel mode is also shown. Below, the complex map of the Morinaga function is compared to that of function BesselJ0.
Ethimology
The name mori or Mori is suggested as sequence of the first 4 letters of the English transliteration of the last name of Makoto Morinaga, interested in the problem, where the Morinaga function is expected to be useful. [1]
Definition
In the most of cases, the Morinaga function can be expressed through the Bessel function,
\(\displaystyle \mathrm{mori}(x)=\frac{J_0(L_1\, x)} {1\!-\!x^2}\)
where \(J_0\) is the zeroth Bessel function, id est, BesselJ0; \(J_0(z)\!=\,\)BesselJ\([0,x]\)
and \(L_1\! \approx \! 2.404825557695773\) is the first zero of BesselJ0, id est, \(L_1\!=\,\)BesselJZero\([0,1]\). In such a way, \(J_0(L_1)\!=\!0\).
At unity, the definition above is not valid, and mori is defined as limit
\(\displaystyle \mathrm{mori}(1)= \lim_{x\rightarrow 1} \frac{J_0(L_1\, x)} {1\!-\!x^2} =\,\) \( \displaystyle \frac{L}{2} J_1(L_1)\approx 0.624229584847753325\)
Origin
Morinaga function appears at the Bessel transform of the principal Bessel mode
\(\mathrm{mode}(x)= J_0(x) \theta(L_1\!-\!x^2)\)
where \(\theta\) is the UnitStep function.
Being converted to the momentum representation, this mode leads to the Bessel transform
\(\displaystyle \int_0^\infty \mathrm{mode}(x) \, J_0( p x)\, x\, \mathrm d x =\,\) \(\displaystyle \int_0^{L_1} J_0(x) \, J_0( p x)\, x\, \mathrm d x =\,\) \(\displaystyle J_1(L_1)\, L_1\, \frac{J_0(p L_1 )}{1\!-\!p^2} =\,\) \(\displaystyle J_1(L_1)\,L_1 \, \mathrm{mori}(p)\)
Factor \(\displaystyle J_1(L_1)\, L_1\approx 1.24846\) is excluded from the expression for the definition of mori on order to make the expression as short as possible. In addition, for the resulting function mori, both, its value at zero and its norm happen to be rational numbers.
Expansion at zero
Expansion at zero of the Morinaga function can be written as follows:
\(\mathrm{mori}(x) \approx 1 + \sum_{m=1}^{M-1} c_m x^{2m} + O(x^{2M}) \)
The first coefficients \(c\) are
\(c_0=1\)
\(c_1=1 - L_1^2/4 ~ \approx - 0.44579649073669613\)
\(c_2=1\!-\! L_1^2/4\!+\!L_1^4/64 \approx 0.07678538241994\)
\(c_3=1\!-\! L_1^2/4\!+\!L_1^4/64\!-\!L_1^6/2304 \approx 0.0004215952205514\)
Approximations for more coefficients can be extracted from the generator of the figure at the top. The series seem to converge at any \(x\), as function mori has no singularities; it is entire function. However, the rounding errors limit the range of applicability of this expansion. With double (or complex double) variables, with \(M\!=\!16\) , while last term with coefficient \(c_{15}\) is taken into account, of order of 15 decimal digits can be obtained at least for \(|x|<2\). For lower precision, say, 4 digits, the range can be extended to \(x\sim 5\); and this precision is still sufficient to plot camera–ready figures. In particular, for the figure at the top; id est, the expansion with 15 terms could be used to evaluate function mori. The range of precise evaluation with this expansion covers the point \(x\!=\!1\), so, no special expansion at unity happen to be necessary for the numerical implementation.
In principole, the expansions at the zeroes of function mori also can be used for the evaluation, but, for the standard double precision, the other expansions do not seem to provide better precision, than the original representation in the definition and the numerical implementation in the C++ built-in function double j0(double x).
Expansion at infinity
Espansion of function mori at infinity follows from that of function BesselJ0:
\(\displaystyle \mathrm{mori}(x) \approx \) \(\displaystyle \sqrt{\frac{2}{L\pi x^{5}}} \left(-1-\frac{128 L^2-9}{128 L^2 x^2}-\frac{32768 L^4-2304 L^2+3675}{32768 L^4 x^4}+O\left(x^{-6}\right)\right) \cos \left(\frac{\pi }{4}-L x\right) +\) \(\displaystyle \sqrt{\frac{2}{L\pi x^{5}}} \left(\frac{1}{8 L x}+\frac{128 L^2-75}{1024 L^3 x^3}+\frac{32768 L^4-19200 L^2+59535}{262144 L^5 x^5}+O\left(x^{-7}\right)\right) \sin \left(\frac{\pi }{4}-L x\right) \) \(\approx \sqrt{\frac{2}{L\pi x^{5}}} \left(-1 -0.9878419092087828/x^2 - 0.991195214492434/x^4 +O\left(x^{-6}\right)\right) \cos \left(\frac{\pi }{4}-L x\right) +\) \( \sqrt{\frac{2}{L\pi x^{5}}} \left( 0.051978822164452966/x + 0.04671246183865335/x^3 + 0.04953613575448617/x^5 +O\left(x^{-7}\right)\right) \sin \left(\frac{\pi }{4}-L x\right) \)
Another expansion at infinity
Another expansion of function mori at large values of the argument follows from the expansion to the Hankel function HankelH1; or from the asymptotic expansion of function kori. The asymptotic approximation can be written as follows:
\(\displaystyle \mathrm{morias}_m(z) = - \sqrt{\frac{2}{\pi L_1}} z^{-5/2} \, G_m(z^2)\, \cos\left( - \frac{\pi}{4} + L_1 z\, F_m(z^2) \right) \)
where
\(G_m(x) = \sum_{n=0}^{m} g_n x^{-n}\)
\(F_m(x) = \sum_{n=0}^{m} f_n x^{-n}\)
Approximations for the coefficients \(f\) and \(g\) are:
\(\begin{array}{l} f_0=1\\ f_1=- 0.021614383628830615865\\ f_2=0.0019465899152260872595\\ f_3=-0.0010834984344719114778\\ f_4=0.001464410164512283719\\ f_5=-0.003628876399615993660\\ f_6=0.01431760830195380729\\ f_7=-0.0824438982874790057\\ f_8=0.652747801052423657\\ f_9=-6.80376838070624330\\ f_{10}=90.322658904953727\\ f_{11}=-1487.942880868968812\\ f_{12}=29785.50901270392374\\ \end{array}\) \(~\) \(\begin{array}{l} g_0=1 \\ g_1=0.989192808185584692068 \\ g_2=0.99228788615079417081 \\ g_3= 0.989481317221334367489\\ g_4= 0.994709980602617872387\\ g_5= 0.97818700495778240956\\ g_6=1.0575251177784290263\\ g_7= 0.5188843197279991625\\ g_8=5.432808917007474985\\ g_9=-52.5640507009104629\\ g_{10}=807.429675670594971\\ g_{11}= -14844.4023379433794\\ g_{12}=328204.367306340176 \end{array}\)
Norm
The squared norm of the Morinaga function appears as \(\mathrm{Nor}=\displaystyle \int_0^\infty \mathrm{mori}(x)^2 \, x\, \mathrm d x\)
It can be expressed through the squared norm of the Bessel mode, as the Bessel transform preserves the norm of the function:
\(\mathrm{NorB}=\displaystyle \int_0^{L_1} \, J_0(x)^2 \, x\, \mathrm d x= L_1^2\, J_1(L_1)^2/2\)
the same squared norm of the Besse mode can be expressed also through its Bessel transform:
\(\mathrm{NorB}=\,\) \(\displaystyle \int_0^\infty \left( J_1(L_1)\, L_1 \frac{J_0(p )}{1\!-\!p^2} \right)^2 \, p\, \mathrm d p =\,\) \(\displaystyle \int_0^\infty \Big( J_1(L_1)\, L_1 \, \mathrm{mori}(p ) \Big)^2 \, p\, \mathrm d p =\,\) \(\displaystyle J_1(L_1)^2 L_1^2 \int_0^\infty \mathrm{mori}(p)^2 \, p\, \mathrm d p\)
The comparison with the First and Second equation in this section gives, that
\(\mathrm{Nor}=\displaystyle \int_0^\infty \mathrm{mori}(x)^2 \, x\, \mathrm d x = \frac{1}{2}\)
Attempts to substitute the deduction above with computation at the Mathematica software failed. In Mathematica language, the squared norm of the Morinaga function can be written as follows:
Integrate[ ( BesselJ[0, p*BesselJZero[0, 1]]/(1 - p^2))^2 p, {p, 0, Infinity}]
The Mathematica software, for this suggests the following expression:
-(Sqrt[Pi]*MeijerG[{{}, {1/2}}, {{0, 1}, {0}}, BesselJZero[0, 1]^2])/2
Only the evaluation with 10 digits helps to guess, that this abracadabra means just 1/2.
Approximations

Fot the numerical calculus, the expansions of mori at zero and at infinity can be used. However, for the better performance, the fitting may have sense. These firing are considered in this section.
Let
\(\displaystyle \mathrm{korifit76}(x)= \prod_{n=2}^7\! \left(1-\frac{L_1^2}{L_n^2}x\right)~ \frac{1+\sum_{n=1}^6 a_n x^n}{1+\sum_{n=1}^6 b_n x^n} \)
where \(L_n=\mathrm{BesselJZero}[0,n]\) and coefficients \(a\) and \(b\) are:
\(a_1=-0.04844698269548584 \)
\(a_2= 0.0010028289633265202 \)
\(a_3= -0.000011428855401098336\)
\(a_4= 7.61813379974462\times 10^{-8}\)
\(a_5= -2.8376606186641804\times 10^{-10}\)
\(a_6= 4.651275051439759\times 10^{-13}\)
\(b_1= 0.03223483760044156\)
\(b_2= 0.0004974915308429358\)
\(b_3= 4.7768603073237505\times 10^{-6}\)
\(b_4= 3.071615607112112\times 10^{-8}\)
\(b_5= 1.292095753771865\times 10^{-10}\)
\(b_6= 2.925186494186955\times 10^{-13}\)
Then,
\(\displaystyle \mathrm{mori}(z) \approx \mathrm{korifit76}(z^2)\)
This approximation is valid in vicinity of the positive part of the real axis, roughly, while \(|Re(z)|\! \le \!L3/L2\approx 6.2\) and\(|\Im(z)|\!<\!2~\), providing of order of 14 significant figures; in this range, the deviation is of order of the rounding errors at use of the complex double variables.
In the range specified, the approximation above seems to be faster and preciser, than the straightforward representation through the Bessel function evaluated with the "machine precision" in "C++" or "Matehmatica". In particular, the approximation above reproduces exactly the first 6 zeros of function mori, since \((L_2/L_1)\approx 2.3~\) to \((L_7/L_1)\approx 8.8~\).
The range of approximation and precision above seems to be sufficient for the preliminary analysis of integrals with function mori, and, in paticular, for the numerical evaluation of the function below\[\mathrm{naga}(t)=2\int_0^\infty \mathrm{mori}(p)^2 \exp(\mathrm i \,t\, p^2)\, p\, \, \mathrm d p\\]
Applications
Morinaga function appears at the guiding of waves by the set of coaxial pinholes. This guiding can be interpreted in terms of the Zeno effect; the dense absorbing is interpreted as a "measurement", and the frequent measurement prevents the particles from entering the outside area from the cylinder formed by the pinholes. For this reason, in the first approximation, the guided mode appears as the principal Bessel mode, and its transform appears as the Morinaga function.
In the paraxial approximation, when the main dependence \(\exp(\mathrm i k z)\) is already "switched-out" from the wave, the propagation from one pinhole to another one is especially easy in the momentum representation:
\(\psi(p,0)=\mathrm{mori}(p )\)
becomes
\(\psi(p,t)=\mathrm{mori}(p ) \exp(- \mathrm i p^2 t)\)
where \(p\) has sense of the scaled transversal wavenumber, and \(t\) has sense of scaled (with another scaling factor) inverse of the distance between pinhoes. The recovery of dimensions requires certain efforts, but this recovery is not so difficult as driving, drawing and drowing of the dimensional parameters through the deduction. One of problems suggested by Makoto Morinaga is the accurate estimate of the loss of the guided mode at the propagation from one pinhole to the next one.
Assuming that the mode remains almost Besselian, the amplitude of the mode at the next pinhole is determined by the scalar product of the propagated mode to the initial mode. It is easier to calculate this scaling product in the momentum representation; id est, to deal with the Morinaga function mori rather than with propagated Bessel mode. The scalar produce of the transformed mode to the initial one is expressed with the transmittance function (or "transparency function")
\(\displaystyle T(t)=2 \int_0^\infty \mathrm{mori}(p )^2 \, \exp(-\mathrm i p^2 t) \, p\, \mathrm d p\)
Factor \(2\) appears as inverse of the squared norm of function mori.
At the strong guiding (\(t\rightarrow 0\)), the loss of the Bessel mode per one pinhole appear as \(1-|T(t)|^2\). In such a way, function \(T\) determines the asymptotic of loss per single pinhole at the strong guiding conditions. In such a way, the consideration of the Morinaga function should give at least the first non-trivial term in the asymptotic expansion of function \(T(t)\) at small \(t\).
The integral above happen to be a little bit slow to evaluate, and the plot of function \(T\) takes certain CPU time. In order to boost the calculus, the new variable of integration is suggested. Let \(p=\sqrt{q}\); then
\(T(t)=\displaystyle \int_0^\infty \mathrm{mori}\big(\sqrt{q}\big)^2\, \exp(- \mathrm i t q) \, \mathrm d q =\,\) \(\displaystyle \int_0^\infty \mathrm{mori}\big(\sqrt{q}\big)^2\, \cos( t\, q) \, \mathrm d q - \mathrm i \displaystyle \int_0^\infty \mathrm{mori}\big(\sqrt{q}\big)^2\, \sin( t\, q) \, \mathrm d q\)
In such a way, the result appears as linear combination of the CosFT and SinFT of function
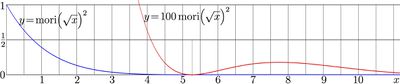
\(U(q )= \mathrm{mori}\big(\sqrt{q}\big)^2 \)
Function \(U\) is important in the application of the Zeno effect and it needs a special name. While this name is still in search, it appears as \(U\). The Explicit plot of function \(U\) is shown in figure at right, \(y\!=\!U(x)\), with blue curve. The plot makes the impression, that \(U(x)\) quickly decays to zero at \(x\approx 5\), and is just zero at the larger values. In order to show, that it is not really so, the additional red curve indicates the same function scaled with factor 100, id est, \(y=100\, U(x)\); then, at least first oscillation, revival of function \(U\) is seen. The additional vertical grid line indicates the first zero of function \(U\), id est, \(x=L_2^2/L_1^2\) \(\approx\) \( 5.2689404316052215\); it is local minimum and zero of function \(U\). The assertional of oscillations of function \(U(x)\) at \(x>5\) may be neglected, and the result may still provide good precision, but this approximation is not asymptotic; there is no small parameter, that would justify this approximation.
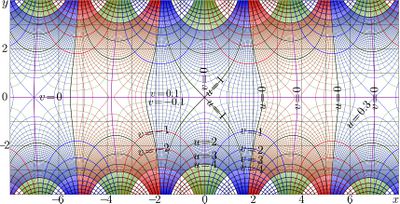
In the integral above, the integrand is quickly oscillating function; the straightforward numerical implementation is slow and not precise. In order to boost the performance, the contour integral may be considered. However, all the functions in the integrand should be implemented for the complex values of the argument. Complex map of function \(U\) is shown in figure at right. It may have sense to give is unique name; name nori should be considered;
\(\mathrm{nori}(z)=\mathrm{mori}\big(\sqrt{z}\big)^2\)
This function is shorn in the complex map at right with levels of constant \(u\) and levels of constant \(v\), for
\(u\!+\!\mathrm i v=\mathrm{mori}\big(\sqrt{x\!+\!\mathrm i y}\,\big)^2\) \(\,=\mathrm{nori}(x\!+\!\mathrm i y)\)
References
- ↑ http://www.academicjournals.org/app/webroot/ebook/journal1414510635_IJPS%20-%2030th%20Oct,%202014%20Issue.pdf#page=12 Makoto Morinaga. Guiding of light with pinholes. hysical Sciences Volume 9 Number 20 30 October, 2014 ISSN 1992-1950, pages 444-453
Keywords
Bessel transform, kori, maga, naga, nori