Yulya function
Yulya function is elementary function such that
- \(\displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\! (1) ~ ~ ~ ~ \mathrm{Yulya}_a(x)= \frac{a\!+\!x}{\sqrt{1-(a\!+\!x)^2}}-\frac{a\!-\!x}{\sqrt{1-(a\!-\!x)^2}} \)
where \(a\) is real parameter. In the simplest case, it is assumed that
- \( -1 < a+x < 1\)
- \( -1 < a-x < 1\)
At the edges of this range, the Yulya function becomes infinite.
The ArcYulya function is just inverse function of Yulya, id est, \(\mathrm{ArcYulya}_a=\mathrm{Yulya}_a^{-1}\) in such a way, that
- \( \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!(2) ~ ~ ~ ~ \mathrm{Yulya}_a\!\Big( \mathrm{ArcYulya}_a(z) \Big) = z\)
- \( \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!(3) ~ ~ ~ ~ \mathrm{ArcYulya}_a\!\Big( \mathrm{Yulya}_a(z) \Big) = z\)
at least for some ranges of \(z\) in vicinity of the real axis.
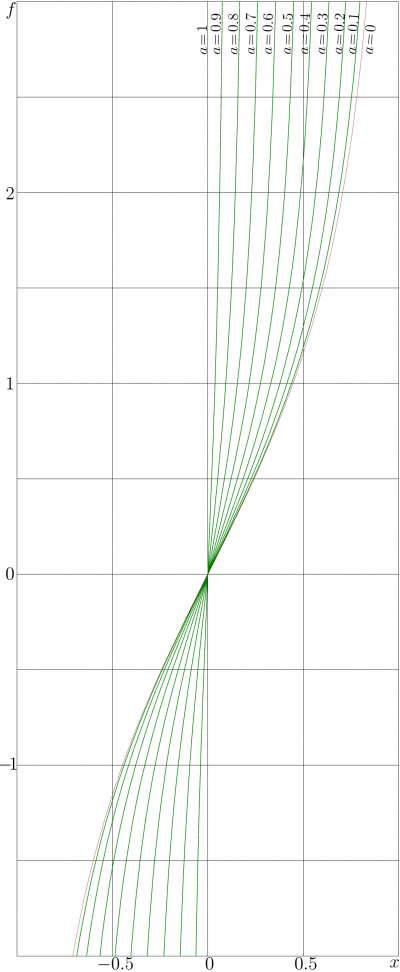
ArcYulya function is used to make plot of Yulya function, shown at right; while the parameter approaches unity, it is more convenient to use value of function as independent variable.
History and applications
The function \(F\) has been suggested in 2011 by Yulya Kuznetsova for planning and optimization of the inclinations of masks at the digital interferometric microscopy with combined aperture [1].
The name Yulya should not be confused with Julia; in particular, the Yulya function is not the same as Julia function and the Yulya set is not Julia set.
Properties of Yulya function
The contour plot of \(f=\mathrm{Yulya}_a(x)\) is shown in the figure at right with lines \(f\!=\!\rm const.\) in the \(x,a\) plane. At \(x\!+\!a=1\), the function becomes infinite. At \(x\!+\!a>1\), the function has complex values; at the figure this range is shaded.
For the analysis of the properties Yulya and the building up the efficient approximations for the inverse function, it may have sense to consider it as holomorphic function of the complex argument.
Being extended to the negative values of \(x\) asn \(a\) the Yulya function and its inverse have the symmetry
- \( \displaystyle \mathrm{Yulya}_a(-\!x)=-\mathrm{Yulya}_a(x)\)
- \( \displaystyle \mathrm{ArcYulya}_a(-\!x)=-\mathrm{ArcYulya}_a(x)\)
- \( \displaystyle \mathrm{Yulya}_{-a}(x)=\mathrm{Yulya}_a(x)\)
- \( \displaystyle \mathrm{ArcYulya}_{-a}(x)=\mathrm{ArcYulya}_a(x)\)
At the range \( -\! 1 \! + \!a < x < 1\!-\! a\), function \(\mathrm{yulya}_a(x)\) is monotonously increasing. Values \(x=\pm (1-a)\) are singular points; \(\mathrm{Yulya}_a(x) \rightarrow + \infty\) at \(x\rightarrow 1\!-\! a\).
Derivative of Yulya function
The straigh-forward use of the Mathematica gives
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\! (4) ~ ~ ~ \mathrm{Yulya}'_a (x)= \frac{(a-x)^2}{\left(1-(a-x)^2 \right)^{3/2}}+\frac{1}{\sqrt{1-(a-x)^2}}+\frac{1}{\sqrt{1-(a+x)^2}}+\frac{(a+x)^ 2}{\left(1-(a+x)^2\right)^{3/2}} \)
and there it is difficult to find any way to force Mathematica to convert is to the simpler expression
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\! (5) ~ ~ ~ \mathrm{Yulya}'_a (x) = \frac{1}{\left(1-(a+x)^2\right)^{3/2}}+\frac{1}{\left(1-(a-x)^2\right)^{3/2}} \)
In particular,
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\! ~ ~ ~ \mathrm{Yulya}'_a (0)= \frac{2}{(1\!-\!a^2)^{3/2}}\)
Expansion at small values of parameter
In the case of small \(|a|\ll 1\),
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\! (6) ~ ~ ~ \mathrm{Yulya}_a (0)= \frac{2x}{\sqrt{1-x^2}}+\frac{3 a^2 x}{\sqrt{1-x^2} \left(x^2-1\right)^2}+\frac{5 a^4 \left(4 x^3+3x\right)}{4 \sqrt{1-x^2} \left(x^2-1\right)^4}+O\left(a^6\right)\)
Yulya function at small values of the argument
Asymptotic expansion at small values of the argument has the form
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\! (7) ~ ~ ~ \mathrm{Yulya}_a(x)= \frac{2 x}{\left(1-a^2\right)^{3/2} }+\frac{\left(4 a^2+1\right) x^3}{\left(1-a^2\right)^{7/ 2}}+\frac{3 \left(8 a^4+12 a^2+1\right) x^5}{4 \left(1-a^2\right)^{11/2}}+ \mathcal O\left(x^7\right) \)
Yulya function at argument approaching the singularity
Another asymptotical expansion of \(\mathrm{Yulya}_a(x)\) can be simplified denoting the new small parameter \(y\) such that \(x=1\!-\!a\!-\!2y^2\). then,
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\! (8) ~ ~ ~ \mathrm{Yulya}_a(1\!-\!a\!-\!2y^2)= \frac{1}{2 y} +\frac{1-2 a}{2 ((1\!-\!a)a)^{1/2}} -\frac{3y}{4} -\frac{y^2}{4 ((1\!-\!a)a)^{3/2} } -\frac{5y^3}{16}+\mathcal{O}\left(y^4\right) \)
which can be expressed also as follows:
- \( \displaystyle \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! (9) ~ ~ ~ \mathrm{Yulya}_a(x)= \frac{1}{2}\Big(\!\frac{1\!-\!a\!-\!x}{2} \!\Big)^{\!\! -1/2} +\frac{1-2 a}{2 ((1\!-\!a)a)^{1/2}} -\frac{3y}{4}\Big(\!\frac{1\!-\!a\!-\!x}{2}\!\Big)^{\!\! 1/2} -\frac{1}{4 ((1\!-\!a)a)^{3/2} }\Big(\!\frac{1\!-\!a\!-\!x}{2}\!\Big) -\frac{5}{16}\Big(\!\frac{1\!-\!a\!-\!x}{2}\!\Big)^{\!\!3/2} +\mathcal{O}\!\Big(\Big(\!\frac{1\!-\!a\!-\!x}{2}\!\Big)^{\!2}\Big) \)
Inverse function, ArcYulya
The flipping of the top plot around the line \(x=f\) gives the graphics of the inverse function of Yulya, id est, \( \mathrm{ArcYulya}_a=\mathrm{ArcYulya}_a^{-1}\). The contour plot of \(f=\mathrm{ArcYulya}_a(x)\) is shown in the \(x,a\) plane in the figure at right with lines \(f=\mathrm{const}.\).
The expansions (7),(8),(9) above can be inverted, giving the asymptotical representation for the ArcYulya.
Small values of parameter
For small values \(|a|\ll 1\), the inversion of (6) gives the asymptotic of ArcYulya function:
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\!\!\!(31) ~ ~ ~ \mathrm{ArcYulya}_a(x)= \frac{x}{\sqrt{4\!+\! x^2}} -\frac{3}{8} a^2 x \sqrt{4\!+\! x^2} +\frac{1 }{128} a^4 x \left(x^2+4\right)^{3/2} \left(7 x^2+3\right) + \mathcal{O}(a^6) \)
Small values of the argument
For small value of the argument of ArcYulya, the inversion of series in (7) gives the espansion in the following form
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\!\!\!(32) ~ ~ ~ \mathrm{ArcYulya}_a(f)= \frac{1}{2}\left(1\!-\!a^2\right)^{\!\!3/2}f -\frac{1}{16} \left(1\!-\!a^2\right)^{\!\!5/2} \left(4 a^2\!+\!1\right) f^3 +\frac{3}{256} \left(1-a^2\right)^{\!\!7/2} \left(24 a^4\!+\!4 a^2\!+\!1\right)f^5 +\mathcal O\left(f^7\right) \)
This expansion can be used for evaluation of \(\mathrm{ArcYulya}_a(f)\) at \((1\!-\!a)f \ll 1\).
Large values of the argument
For positive \(а\), for large values of the argument of ArcYulya, the inversion of series in (8) gives the expansion in the following form:
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! (33) ~ ~ ~ \mathrm{ArcYulya}_a(f)= 1\!-\!a-\frac{1}{2 f^2}+\frac{2 a-1}{2 \sqrt{(1\!-\!a) a} f^3}+\frac{3 \left(5 a^2-5 a+1\right)}{8 (a-1) a f^4}+\frac{56 a^3-84 a^2+36 a-3}{16 ((1\!-\!a) a)^{3/2} f^5}-\frac{5 \left(21 a^3-42 a^2+28 a-6\right)}{16 \left((1\!-\!a)^2 a\right) f^6}+\mathcal O\Big(\Big(\frac{1}{ f}\Big)^7\Big) \)
Such an expansion can be used for the evaluation of \(\mathrm{ArcYulya}_a(f)\) at \(|(1\!-\!a)f^2| \gg 1\).
Fitting of ArcYulya
Some of the asymptotic properties of expansions (31) and (33) are combined in the fit
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! (35) ~ ~ ~ \mathrm{ArcYulya}_a(f)\approx \frac{(1-a)f} {\sqrt{\frac{4}{(1-a) (a+1)^3}+f^2}} \)
Fit (33) reproduces correct first and second derivatives of ArcYulya at zero, and it tends to the correct value \(1\!-\!a\) as the argument goes to infinity. For \(0\!<\!a\!<\!0.9~\), such a fit returns at least two significant decimal digits for any real \(f\).
The Matlab implementation of fit (35) may have the following form:
function x=arcyulya0(a,f) x=((1-a).*f) ./ sqrt( 4./((1-a).*(1+a).^3) + f.*f)
Such a text can be stored in file arcyulya0.m in the working matlab directory; then the rough approximation for the \(\mathrm{ArcYulya}_a(f)\) can be specifying with code arcyulya0(a,f) .
The fit (35) can be improved, adding more terms in the numerator and the argument of the radical in the denominator. Practically, the adjusting of the approximation with the straightforward Newton method described below seems to be more efficient
Iterations
The fit (35) gives the good approcimation, that can be used to get even more prefise estimate of \(x=\mathrm{ArcYulya}_a(f)\) iterating assignment
- \( \displaystyle \!\!\!\!\! \!\!\!\!\! \!\!\!\!\! \!\!\!\!\!(39) ~ ~ ~ x = x + \frac{f-\mathrm{Yulya}_a(x)}{\mathrm{Yulya}_a^\prime (x)}\)
Using the initial approximation (35), very few iterations are sufficient to get several correct digits in the resulting implementation of ArcYulya. Practically, to get the camera-ready quality of the pictures, two iterations are sufficient; and seven iterations give approximately 14 correct decimal digits.
Implementation of Yulya and ArcYulya
C++ implementation
The derivative of Yulya can be implemented as follows:
#define DB double
DB Yulyap(DB a, DB x){ DB p,m; p=a+x; m=a-x; p=1.-p*p; m=1.-m*m;
return 1./(p*sqrt(p))+1./(m*sqrt(m));}
Then, using the implementation of Yulya and Yulyap, the ArcYulya can be implemented as follows:
DB ArcYulya0(DB a, DB f){ DB m=1.-a; DB p=1.+a;
return m*f / sqrt( 4./(m*p*p*p) + f*f );}
DB ArcYulya7(DB a, DB f){ int n; DB y=ArcYulya0(a,f);
for(n=0;n<7;n++) y+=(f-Yulya(a,y))/Yulyap(a,y); return y;}
The figures above are generated with such codes; the codes are supplied also at the descriptions (the figures are clickable). The C++ implementations of Yulya and ArcYulya is simple; the conversion of the algorithms to other languages should not be difficult.
Matlab implementation
From the formulas above, one may construct the matlab implementation of Yulya and ArcYulya:
function f=yulya(a,x) f=(a+x)./sqrt(1-(a+x).^2) - (a-x)./sqrt(1-(a-x).^2) ;
function f=yulyap(a,x) f= (1-(a+x).^2).^(-3/2)+(1-(a-x).^2).^(-3/2);
function x=arcyulya(a,f) x=((1-a).*f) ./ sqrt( 4./((1-a).*(1+a).^3)+f.*f); x=x+(f-yulya(a,x))./yulyap(a,x); x=x+(f-yulya(a,x))./yulyap(a,x); x=x+(f-yulya(a,x))./yulyap(a,x); x=x+(f-yulya(a,x))./yulyap(a,x);
With these implementations one may plot
yulya(a,arcyulya(a,x))-x
and
arcyulya(a,yulya(a,x))-x
in the x,a coordinates and check that these quantities are really small.
Conclusion
The mathematica(software) is used to get the asympotical approximation.
The independent test and/or corrections of the matlab implementation should be greatly appreciated.
References
http://www.chtm.unm.edu/publications/pub280.pdf Yuliya Kuznetsova, Alexander Neumann, and S. R. J. Brueck. Solid-immersion imaging interferometric nanoscopy to the limits of available frequency space. Jour. Opt. Soc. Amer. A29, 772-781 (2012).