File:SuExp6termsTestQ2mapT.png

File
File history
File usage
Metadata

Size of this preview: 607 × 599 pixels. Other resolutions: 243 × 240 pixels | 1,544 × 1,524 pixels.

Original file ‎(1,544 × 1,524 pixels, file size: 191 KB, MIME type: image/png)

Summary

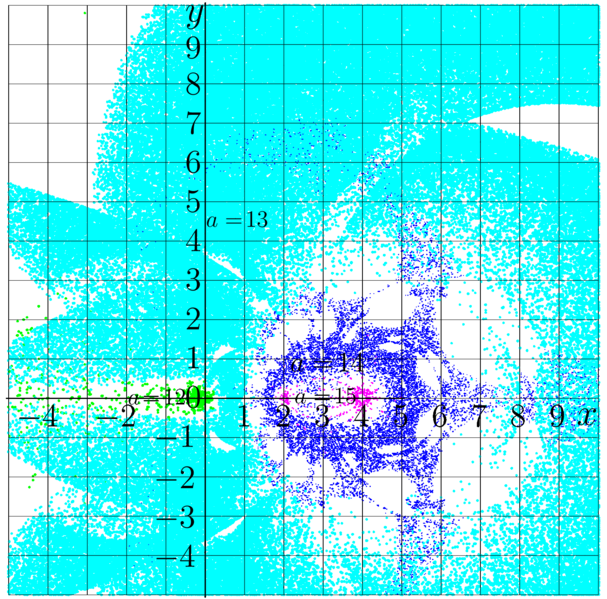
Testing of compatibility of the implementations of the infinitely growing SuperExponential \(F\) and the corresponding growing AbelExponential \(G\) for base \(b \in (1,\exp(1/\mathrm e))\).

For the first tests, value \(b=\sqrt{2} \) is chosen: for this specific value, the efficient implementations of the superfinctions and the abelfuncitons are aleady loaded, Sqrt2f21e.cin, Sqrt2f21l.cin, Sqrt2f23e.cin, Sqrt2f43e.cin, Sqrt2f45e.cin, Sqrt2f45l.cin.

They are described in book «Superfunctions»^[1], 2020.

The map shows agreement function \[ a(z)=- \Re\!\left(\lg\left( \frac {F(G(z))-z} {F(G(z))+z} \right) \right) \] in plane \(z=x+\mathrm i y\), where \(F\) and \(G\) are implemented using the asymptotic expansions with 6 terms taken into account.

The picture suggests, that with 6 terms taken into account in the asymptotics of the functions, of order of 13 significant figures can be calculated using the complex double variables.

C++

/* Routines from ado.cin, filog.cin, Conrec6.cin, Tania.cin should be also loaded.*/

// c++ -std=c++11 SuExp6termsTestQ2map.cc -O2 -o SuExp6termsTestQ2map
// c++ -std=c++11 18.cc -O2 -o 18
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
using namespace std;
#include <complex>
typedef complex<double> z_type;
#define Re(x) (x).real()
#define Im(x) (x).imag()
#define I z_type(0.,1.)
//#include "conto.cin"
#include "ado.cin"
#include "filog.cin"
#include "Conrec6.cin"
//	DB B=1.010;  // from 10 to 12 digits along the real axis.
//	DB B=1.050;  // still proivdes 12 digits along the real axis
//	DB B=1.10;  // still proivdes 12 digits along the real axis
//	DB B=1.1046;  // still proivdes 12 digits along the real axis
//	DB B=1.1048;  // still proivdes 12 digits along the real axis
//	DB B=1.105;  // still proivdes 12 digits along the real axis
//	DB B=1.106;  // still proivdes 12 digits along the real axis
//	DB B=1.108;  // still proivdes 12 digits along the real axis
//	DB B=1.11;  // still proivdes 12 digits along the real axis
//	DB B=1.12;  //  still proivdes 12 digits along the real axis
//	DB B=1.13;  //  still proivdes 12 digits along the real axis
//	DB B=1.2;  // 
//	DB B=1.3;  // 
//	DB B=1.4;  // 
//	DB B=1.42;  // almpst the same
  DB B=sqrt(2.); // 1.4142135623730951 13 digits for Re(z)>1)
//	DB B=1.413 ; //  still proivdes 12 digits along the real axis
//	DB B=1.414 ; //  still proivdes 12 digits along the real axis
//	DB B=1.44 ; //  11 digits for Re(z) > 4 ; loss of preciion
//	DB B=1.44444 ; //  still makes the comlex map
// Warning: B shoud be less than  exp(1/e) \approx 1.4446678610
DB S=log(B); 	//	Warning: many GLOBAL VARIABLES
DB Q=Re(Filog(S-I*1.e-14)); // in Book, it is fixed point  L
#define T(z) (exp(S*z))
#define Tm(z) (log(z)/S)
DB T0=T(Q); //Do not confuse T0 with function T; it is just test.
DB T1=S*T0; // T'(Q) 
DB T2=S*T1; // T''(Q) 
DB T3=S*T2; // T'''(Q) 
DB T4=S*T3; // T''''(Q) 
DB T5=S*T4; // T'''''(Q) 
DB T6=S*T5; // T''''''(Q) 
DB K=log(T1); // in Book, k by formula (6.9) // but here, the Global variables are UPPERCASE.
//DB Xmin=-8./K; // for 4 coefficienta, estimate: log(10^-15)/5/K; exp(5Kx)  should be ~ 10^-15 
//DB Xmin=-6./K; // empiric for 6 coefficients. 
DB Xmin=-5./K; // empiric for 6 coefficients. 
DB iP=2*M_PI/K; // in Book, (9.7), imahinary period.
//z_type e=exp(K*z) //in in Book, it is \varepsiolon by (6.3) .. oops.. I cannot assign it here, I do not know z. 
DB A0=Q;
DB A1=1.;
DB A2=.5*T2/(T1*(T1-1.));
DB A3=(T2*A2+T3/6.)/((T1*T1-1.)*T1);
DB A4 = ( T2*(A3+A2*A2/2.) + T3*A2/2. + T4/24. ) / ((T1*T1*T1-1.)*T1);
DB A5 = ( T2*(A4+A2*A3)+ T3*(A3+A2*A2)/2. + T4*A2/6. + T5/120.) / ((T1*T1*T1*T1-1.)*T1);
DB A6 = ( T2*(A5+A2*A4+A3*A3/2.)+ T3*(A4+2.*A2*A3)/2. + T4*(A3+A2*A2)/6. + T5*A2/24.+T6/720.) / ((T1*T1*T1*T1*T1-1.)*T1);
DB U0=Q;
DB U1=1.;
DB U2=-A2;
DB U3=2.*A2*A2-A3;;
DB U4=5.*A2*A3-A4-5.*A2*A2*A2;
DB U5=6.*A2*A4+3.*A3*A3+14*A2*A2*A2*A2-A1*A1*A1*A5-21.*A2*A2*A3;
DB U6=7.*A2*A5+7.*A3*A4+84*A2*A2*A2*A3-A6-28.*A2*A3*A3-42.*A2*A2*A2*A2*A2-28.*A2*A2*A4;

z_type F0(z_type z){ z_type e=exp(K*z);
return Q+e*(1.+e*(A2+e*(A3+e*(A4+e*(A5+e*A6)))));
}

z_type Fn(z_type z){ z_type c; DB x=Re(z); int n,N;
		N=int(x-Xmin); 
		if(N<1) return F0(z); 
		c= F0(z-double(N));
		for(n=0;n<N;n++) c=exp(S*c);
		return c;
		}

z_type G0(z_type z){ 
	z_type v=z-Q;
	z_type c = v*(1.+v*(U2+v*(U3+v*(U4+v*(U5+v*U6)))));
	return log(c)/K;
	}

z_type Gn(z_type z) // WARNING! Q is global; Tm is also just defined above..
{ int n;
for(n=0;n<31;n++)
		{ 
	//	if(abs(z-Q)<2.e-3) return G0(z)+(0.+n);
	//	if(abs(z-Q)<.005) return G0(z)+(0.+n);
		if(abs(z-Q)<.006) return G0(z)+(0.+n);
		z=Tm(z); 
		}
return G0(z)+(0.+n);
}

DB Xzero=Re(Gn(Q+1.));

z_type G(z_type z) {return Gn(z)-Xzero; }

z_type F(z_type z) {return Fn(z+Xzero); }

int main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d; 
printf("B, S, Q   : %18.16lf %18.16lf %19.16lf\n",B,S,Q); 
printf("T0,T1,K,IP: %18.16lf %18.16lf %19.16lf %19.16lf\n",T0,T1,K,iP); 
printf("T2,A2,U2  : %18.16lf %18.16lf %19.16lf\n",T2,A2,U2); 
printf("T3,A3,U3  : %18.16lf %18.16lf %19.16lf\n",T3,A3,U3); 
printf("T4,A4,U4  : %18.16lf %18.16lf %19.16lf\n",T4,A4,U4); 
printf("T5,A5,U5  : %18.16lf %18.16lf %19.16lf\n",T5,A5,U5); 
printf("T6,A6,U6  : %18.16lf %18.16lf %19.16lf\n",T6,A6,U6); 
// getchar();
int M=501,M1=M+1;
int N=751,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("SuExp6termsTestQ2map.eps","w");ado(o,1524,1520);
//FILE *o;o=fopen("SuExp4termsTestQ2map.eps","w");ado(o,1524,1520);
#define M(x,y)fprintf(o,"%9.6lf %9.6f M\n",0.+x, 0.+y);
#define L(x,y)fprintf(o,"%9.6lf %9.6f L\n",0.+x, 0.+y);
fprintf(o,"510 510 translate\n 100 100 scale 2 setlinecap 1 setlinejoin\n");
DO(m,M1) X[m]=-5.+.03*(m-.5);
DO(n,250)Y[n]=-5.+.02*(n-.1);
        Y[250]=-.00001;
        Y[251]= .00001;
for(n=252;n<N1;n++) Y[n]=-5.+.02*(n-1.);

DO(m,M1)DO(n,N1){g[m+M1*n]=9999; f[m+M1*n]=9999;}
DO(m,M1){x=X[m]; //printf("%5.2f\n",x);
DO(n,N1){y=Y[n]; z=z_type(x,y); 
// c=Tania(z_type(-1.,-M_PI)+log(z))/(-z); 
//c=Filog(z);
//c=exp(z);
//c=F(z);
//c=T(F(z-1.));
//c=Fn(z);
c=G(z);
//c=F(z);
//c=Gn(z);
c=F(c);
c=-log10((z-c)/(z+c));
p=Re(c);q=Im(c); 
if(p>-201. && p<201. && q>-201. && q<201. ){ g[m+M1*n]=p;f[m+M1*n]=q;}
       }}
fprintf(o,"1 setlinejoin 1 setlinecap\n"); p=5.;q=1;
/*
for(m=-10;m<10;m++)for(n=2;n<10;n+=2)Conrec6(o,f,X,Y,M1,N1,(m+.1*n), q); fprintf(o,".008 W 0 .6 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)Conrec6(o,g,X,Y,M1,N1,-(m+.1*n), q); fprintf(o,".008 W .9 0 0 RGB S\n");
for(m=0;m<10;m++) for(n=2;n<10;n+=2)Conrec6(o,g,X,Y,M1,N1, (m+.1*n), q); fprintf(o,".008 W 0 0 .9 RGB S\n");
for(m=1;m<21;m++) Conrec6(o,f,X,Y,M1,N1, (0.-m),p); fprintf(o,".02 W .9 0 0 RGB S\n");
for(m=1;m<21;m++) Conrec6(o,f,X,Y,M1,N1, (0.+m),p); fprintf(o,".02 W 0 0 .9 RGB S\n");
                  Conrec6(o,f,X,Y,M1,N1, (0. ),p); fprintf(o,".02 W .6 0 .6 RGB S\n");
for(m=-20;m<21;m++) Conrec6(o,g,X,Y,M1,N1, (0.+m),p); fprintf(o,".02 W 0 0 0 RGB S\n");
p=2;
Conrec6(o,g,X,Y,M1,N1, 30 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 40 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 50 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1,-30 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1,-40 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1,-50 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,f,X,Y,M1,N1,-30 ,p); fprintf(o,".02 W .9 0 0 RGB S\n");
Conrec6(o,f,X,Y,M1,N1,-40 ,p); fprintf(o,".02 W .9 0 0 RGB S\n");
Conrec6(o,f,X,Y,M1,N1,-50 ,p); fprintf(o,".02 W .9 0 0 RGB S\n");
Conrec6(o,f,X,Y,M1,N1, 30 ,p); fprintf(o,".02 W 0 0 .9 RGB S\n");
Conrec6(o,f,X,Y,M1,N1, 40 ,p); fprintf(o,".02 W 0 0 .9 RGB S\n");
Conrec6(o,f,X,Y,M1,N1, 50 ,p); fprintf(o,".02 W 0 0 .9 RGB S\n");
*/
p=1;
Conrec6(o,g,X,Y,M1,N1, 1 ,p); fprintf(o,".1 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 2 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 3 ,p); fprintf(o,".1 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 4 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 5 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 6 ,p); fprintf(o,".1 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 7 ,p); fprintf(o,".02 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 8 ,p); fprintf(o,".04 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 9 ,p); fprintf(o,".04 W 0 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 10 ,p); fprintf(o,".06 W 1 0 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 11 ,p); fprintf(o,".06 W .6 .6 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 12 ,p); fprintf(o,".06 W 0 1 0 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 13 ,p); fprintf(o,".06 W 0 1 1 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 14 ,p); fprintf(o,".02 W 0 0 1 RGB S\n");
Conrec6(o,g,X,Y,M1,N1, 15 ,p); fprintf(o,".03 W 1 0 1 RGB S\n");

for(m=-5;m<11;m++){M(m,-5)L(m,10)}
for(n=-5;n<11;n++){M( -5,n)L(10,n)}
fprintf(o,".01 W 0 0 0 RGB S\n");
M(-5.06,0) L(5.06,0)
M(0,-5.06) L(0,10.06) fprintf(o,".03 W 0 0 0 RGB S\n");

fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
     system("epstopdf SuExp6termsTestQ2map.eps"); 
     system(    "open SuExp6termsTestQ2map.pdf"); //for mac
}

Output

At the run, the code above produces the following output:

B, S, Q   : 1.4142135623730951 0.3465735902799727  3.9999999999999987
T0,T1,K,IP: 3.9999999999999991 1.3862943611198906  0.3266342599782809 19.2361490420428574
T2,A2,U2  : 0.4804530139182014 0.4485874311952613 -0.4485874311952613
T3,A3,U3  : 0.1665123259944648 0.1903722467978068  0.2120891200549198
T4,A4,U4  : 0.0577087746457709 0.0778295765369683 -0.1021843675069717
T5,A5,U5  : 0.0200003372196427 0.0309358603057080  0.0496986830373718
T6,A6,U6  : 0.0069315886770217 0.0114140886054668 -0.0236995531625204

The values above agree with those from Table 9.1 at page 107 of book «Superfunctions» ^[1], 2020.
Superexponentials to this base (\(b\!=\!\sqrt{2}\)) are considered also at Mathematics of Computations ^[2], 2010.

Latex

\documentclass[12pt]{article}
\paperwidth 1550pt
\paperheight 1530pt
\usepackage{graphicx}
\usepackage{rotating} 
\topmargin -100pt
\textheight 2750pt
\oddsidemargin -80pt
\textwidth 2512pt
\newcommand{\ing}{\includegraphics}
\newcommand{\sx}{\scalebox}
\newcommand{\rot}{\begin{rotate}}
\newcommand{\ero}{\end{rotate}}
\parindent 0px
\begin{document}
\sx{1}{\begin{picture}(1540,1540)
%\put(20,20){\ing{SuExp4termsTestQ2map}}
\put(20,20){\ing{SuExp6termsTestQ2map}}
\put(480,1494){\sx{8}{\(y\)}}
\put(480,1400){\sx{8}{\(9\)}}
\put(480,1308){\sx{8}{\(8\)}}
\put(480,1208){\sx{8}{\(7\)}}
\put(480,1108){\sx{8}{\(6\)}}
\put(480,1008){\sx{8}{\(5\)}}
\put(480, 908){\sx{8}{\(4\)}}
\put(480, 808){\sx{8}{\(3\)}}
\put(480,708){\sx{8}{\(2\)}}
\put(480,608){\sx{8}{\(1\)}}
\put(480,508){\sx{8}{\(0\)}}
\put(400,408){\sx{8}{\(-1\)}}
\put(400,302){\sx{8}{\(-2\)}}
\put(400,202){\sx{8}{\(-3\)}}
\put(400,102){\sx{8}{\(-4\)}}
\put( 50,460){\sx{8}{\(-4\)}}
\put(250,460){\sx{8}{\(-2\)}}
%\put(360,470){\sx{8}{\(-1\)}}
\put(610,460){\sx{8}{\(1\)}}
\put(710,460){\sx{8}{\(2\)}}
\put(810,460){\sx{8}{\(3\)}}
\put(910,460){\sx{8}{\(4\)}}
\put(1010,460){\sx{8}{\(5\)}}
\put(1110,460){\sx{8}{\(6\)}}
\put(1210,460){\sx{8}{\(7\)}}
\put(1310,460){\sx{8}{\(8\)}}
\put(1410,460){\sx{8}{\(9\)}}
\put(1480,464){\sx{9}{\(x\)}}

\put(84,540){\sx{13}{\(a\!=\!12\)}}
\put(740,1120){\sx{13}{\(\!a=\!13\)}}
\put(730,570){\sx{13}{\(\!a=\!14\)}}
\end{picture}}
\end{document}

References

↑ ^1.0 ^1.1 https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.
↑ https://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
https://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.

Keywords

[[]] «AbelExponential», «Abel function», «Abelfunction», «Agreement», «Base sqrt2», «Exponential», «PowerSeriesInversion», «SuperExponential», «Superfunction», «Superfunctions»,

File history

Click on a date/time to view the file as it appeared at that time.

	Date/Time	Thumbnail	Dimensions	User	Comment
current	09:38, 11 February 2026		1,544 × 1,524 (191 KB)	T (talk \| contribs)	Corrected misprints in the code of the main routine. Reduced number of iterates. Reduced font-size of the labels.
	04:09, 10 February 2026		1,544 × 1,524 (258 KB)	T (talk \| contribs)	{{oq\|SuExp6termsTestQ2mapT.png\|Original file ‎(1,544 × 1,524 pixels, file size: 258 KB, MIME type: image/png)\|400}} Testing of compatibility of the implementations of the infinitely growing SuperExponential \(F\) and the corresponding growing AbelExponential \(G\) for base \(b \in (1,\exp(1/\mathrm e))\). For the first tests, value \(b=\sqrt{2} \) is chosen: for this specific value, the efficient implementations of the superfinctions and the abelfuncitons are aleady loaded, [[Sqrt2...

You cannot overwrite this file.

File usage

There are no pages that use this file.

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

File change date and time	18:37, 10 February 2026

[book-1] 1.0 ^1.1 https://mizugadro.mydns.jp/BOOK/468.pdf D.Kouznetsov. Superfunctions. Lambert Academic Publishing, 2020.

[2] ttps://www.ams.org/journals/mcom/2010-79-271/S0025-5718-10-02342-2/home.html
https://mizugadro.mydns.jp/PAPERS/2010sqrt2.pdf D.Kouznetsov, H.Trappmann. Portrait of the four regular super-exponentials to base sqrt(2). Mathematics of Computation, 2010, v.79, p.1727-1756.

[1]

[2]