Модель коллапсирующей экономики
Модель коллапсирующей экономики, или "Простая модель коллапсирующей экономики", есть статья, ТОРИфицируемая из латексной версии [1] и загружаемая ниже для удобства цитирования.
Первая же ссылка выше изменает нумерацию упоминаемых линков, так что нумерация здесь отличается от оригинала. Есть и иные отличия; в частности, викилинки на другие статьи в ТОРИ, рисунок 0 справа, ключевые слова и категории.
Abstract
Рассмотрена временная эволюция стоимости российского рубля в 2014 году. Стоимость рубля в центах США выражена как функция времени. Предложены аппроксимации этой стоимости в терминах элементарных фунцкий. Описана простая экономическая модель, в которой одна из этих функций получается как решение дифференциального уравнения. Сингулярность решения указывает на естественную границу области применимости этой модели.
Introduction
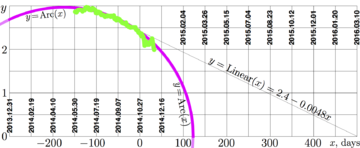
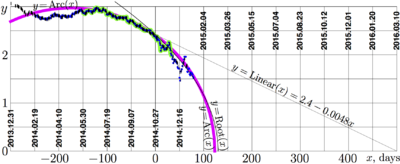
Fig.1: Value \(y\) of Russian rouble, measured in the USA cents, versus time \(x\): preliminary data and the approximations
Эта статья мотивирована наблюдением сильных колебаний стоимости российского рубля как функции времени в течение 2014 года. Эти колебания выглядят похоже, независимо от того, измеряется ли стоимость рубля в долларах США, в евро или в йенах (см.статью Approximations of ruble); поэтому здесь я ограничиваюсь анализом стоимости рубля только в одних единицах, а именно, в долларах США. С момента создания современного рубля в конце 20го века до 2014 года, рубль уже достаточно обесценился; поэтому, чтобы избежать лидирующих (и незначимых) нулей в оценках, стоимость здесь выражается не в самих долларах, а в центах. В частности, такие единицы измерения использованы в фигуре 1.
В 2014 году, стоимость рубля колеблется более чем вдвое; причем на масштабах порядка двух недель относительные колебания превышают 30 процентов. Эти колебания существенно превышают обычную "вилку", которая необходима обменникам валюты для рентабельности, и возникает вопрос о том, почему валютные спекулянты не могут сгладить такие быстрые и такие сильные колебания стоимости российской валюты.
Поведение курса рубля, представленное на рисунках, можно описать простыми элементарными функциями; причем на масштабах порядка месяца, удачные аппроксимации (и даже экстраполяции) дают примерно две значащие цифры. Вопрос о том, какие экономические модели могут стоять за этими функциями, представляет научный, академический интерес. Одна из таких моделей описана в этой статье.
Fitting of experimental data
Нет сомнения в том, что в 2014 году рубль быстро дешевеет: к концу 2014 года, его стоимость проваливается до половины от его стоимости в начале года [2][3].
Примерно к 2014.10.27, были загружены экспериментальные данные о стоимости рубля по отношению к доллару США от [2]. Эти данные представлены на рисунке 1 толстой зеленой кривой. На рисунке по оси абсцисс отложено время \(x\) измеряемое в днях с момента начала проекта, то есть с 2014.10.27; ось ординат \(y\) имеет смысл стоимости российского рубля, измеренной в центах США. Примерно через месяц, 2014.11.29, эти данные были слегка расширены; новые значения были загружены с того же сайта. Разумеется, 2014.10.27, только данные для \(x\le 0\) были доступны, и эти значения были аппроксимированы линейной функцией, которая здесь названа "Linear" и показана на рисунке 1 тонкой чёрной прямой:
\(y=\mathrm{Linear}(x)= 2.4-0.00048x\)
Дата изготовления этой аппроксимации, то есть 2014.10.27 выбрана как ноль на оси абсцисс. Эту дату следует считать датой начала научного проекта. Линейная (а не экспоненциальная) аппроксимация дешевеющей валюты оказалась удачной и держится в качестве верхней границы как для отрицательных значений координаты, так и для положительных. Это странное наблюдение сделало из эволюции рубля интересную научную проблему.
Вскоре, для линейной аппроксимации было предложено название "Программа 500 дней", и эта аппроксимация была раскритикована. Основной критики были заявления о том, что такой сложный процесс как инфляция не может следовать прямой линии (и навряд ли может быть описан двухпараметрической функцией).
Примерно через месяц после начала обсуждения линейной аппроксимации, а именно 2014.11.29, то есть при \(x=32\), эта критика была принята во внимание. Была предложена новая трехпараметрическая аппроксимация в виде эллипса:
\(y=\mathrm{Arc}(x)= c \sqrt{(a+x)(b-x)}\)
Значения параметров \(a\), \(b\) и \(c\) несkолько "гуляют" в зависимости от того, на каком интервале аппроксимируются экспериментальные данные. Наиболее устойчивой, стабильной (аппроксимация держится уже несколько месяцев) оказалась комбинация параметров, предложенная изначально, то есть 2014.11.29, а именно
\(~a\!=\!471~\), \(b\!=\!123~\), \(~c\!=\!0.01~\);
именно для этой комбинации функция Arc показана на рисунке 1 толстой розовой дугой. При выбранном отношении масштабов по осям абсцисс и ординат, для \(~c\!=\!0.01~\), этот эллипс выглядит как дуга окружности. Чтобы подчеркнуть этот факт, эта окружность слегка продолжена ниже оси абсцисс, в область "отрицательного" листа многолистной функции sqrt.
Возможно, имела место наблюдательная селекция: именно при этом отношении масштабов, эллипс выглядит как дуга окружности, и такую аппроксимацию легко угадать, глядя на график. Однако, раз уж такая дуга оказалась столь наглядной, этот масштаб здесь сохранен и для других рисунков.
При измерении в центах стоимости сторублевки, коэффициент \(c\) оказывается равным единице, создавая обманчивое впечатление, что использована двухпараметрическая (а не трехпараметрическая) фитирующая функция. Разумеется оси координат на рисунке 1 имеют разный смысл, и поэтому формально аппроксимирующая кривая должна считаться эллипсом, а не окружностью.
Согласие с экспериментом эллиптической аппроксимации Arc оказалось очень хорошим. Это согласие имеет место для гораздо более широкой области значений аргумента, чем область данных, показанных на рисунке 1. Область расширена как в сторону уменьшения значений аргумента, так и в сторону увеличения; с течением времени, всё новые и новые экспериментальные данные становится доступны. Эти новые данные показаны на рисунке 2.
Рисунок 2 является усложнением рисунка 1. К кривым и данным рисунка 1 добавлены данные с 2014.02.20 по 2015.01.14 включительно; эти данные показаны синими точками; они взяты с того же сайта [2].
Кроме того, в рисунке 2 использованы данные с сайта [3], эти данные показаны чёрными барами.
Кроме того, добавлена аппроксимация Root,
\(\mathrm{Root}(x)=0.01\sqrt{450(130-x)~}\)
Рисунок 2 показывает, что область применимости аппроксимации Arc оказалась существенно шире, чем область значений аргумента, для которой она предложена. Tакая неожиданная эффективность этой аппроксимации порождает искушение найти модель, которая, хотя бы асимптотически, воспроизводила корневую особенность фунkции Arc при \(x=b\), то есть при некоторых значениях параметров воспроизводила бы функцию Root как оценку стоимости рубля. Такая модель предложена в следующей секции.
Model
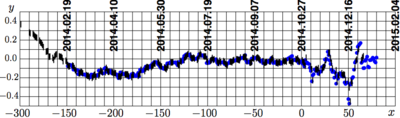
Отклонение экспериментальных данных от эллиптической аппроксимации Arc показано на рисунке 3. В левой части рисунка отклонение показывает вполне регулярный тренд, который можно интерпретировть в связи с историческими событиями вторжения в Украину и раздачи боевых наград За возвращение Крыма 20.02.14-18.03.14 (и соответствующими затратами, требовавшими значительной эмиссии национальной валюты). В правой части рисунка 3, отклонение носит нерегулярный характер, хотя в этом отклонении можно увидеть слабые квази-периодические колебания с периодами порядка месяца и ещё более слабые осцилляции с периодом порядка двух недель с амплитудой, сравнимой с погрешностью экспериментальных данных. Масштаб отклонений мал по сравнению с исследуемой величиной даже в области, куда приближение Arc экстраполируется. Малость этого отклонения указывает на то, что за корневой особенностью аппроксимации Arc может стоять простая экономическая модель коллапсирующей экономики. Такая модель предлагается ниже. Сперва перечисляются исходные допущения, а потом на основе этих допущений выводится уравнение.
1. Предположим, в некоторой стране коррупция приобрела не просто масштабные формы, но стала привычным, обыденным явлением, которое характеризует саму жизнь общества [4].
2. Предположим, что мафия стала настолько могущественной, что она имеет возможность приобрести полу-легальный печатный станок, производящий полулегальную национальную валюту. Термин "полулегальный" здесь указывает, что эмиссия осущетвляется неконтролируемо, в обход действующего законодательства, но ввиду коррупции, указанной в первом допущении, лица, ответственные за выпуск этой валюты, не могут быть привлечены к уголовной ответственности, как более мелкие фальшивомонетчики; то есть изготовляемая ими валюта принимается в магазинах, банках и обменниках наравне с легальной. Для модели не важно, как технически осуществляется эмиссия таких полулегальных денег; для экономики (и для этой модели) такая эмиссия эквивалентна тому, как если бы национальную валюту руководству мафии поставлял непосредственно Аллах [5].
3. Предположим, что выпуск полулегальной валюты определяется потребностями мафии в деньгах, и потребление этой мафии, будучи выражено в иностранной валюте, остается постоянным. С учетом инфляции, скорость увеличения количества национальной валюты можно аппроксимировать уравнением
\( N'=\frac{\alpha}{f} \)
где \(N\) есть количество полулегальной национальной валюты, для определенности, рублей, в обращении, \(f\) есть рыночная цена этой валюты, выраженная, например, в американских центах, а \(\alpha\) есть постоянный коэффициент пропорциональность, выражающий аппетиты мафии.
4. Предположим, что Центральный Банк, зная о выпуске полулегальных денег, пытается конкурировать с мафией, осуществляя собственную, чуть более легальную эмиссию денег так, чтобы скорость убывания стоимости \(f=f(x)\) рубля была пропорциональна скорости \(N'\) полулегальной эмиссии. Эта пропорциональность может быть выражена уравнением
\(f'(x) = - \beta N'\)
где \(\beta\) есть постоянный коэффициент, который выражает стремление Центрального Банка хоть как-то повлиять на полулегальную эмиссию денег.
На основе предположений 1-4, можно построить простую экономическую модель. Из уравнений выше я получаю, что
\( f'(x)=-\frac {\alpha \beta}{f(x)} \)
Это уравнение легко решается:
\(f(x)f'(x)=-\alpha \beta\)
\(\frac{ \mathrm d f(x)^2}{\mathrm d x}= - 2 \alpha \beta\)
\(f(x)^2=-2\alpha \beta x + \gamma\)
где \(\gamma\) есть постоянная интегрирования. Тогда
\( f(x)=\sqrt{\gamma-2\alpha \beta x} \)
сравнивая это решение с аппроксимацией
\(\mathrm{Root}(x)=0.01\sqrt{450(130-x)}\)
показанной тонкой черной кривой на рисунке 2, можно оценить параметры модели:
\(\gamma \approx .01^2\times 450\times 130/2 = 2.9\approx 3 ~\) , \(~ \alpha\beta \approx 450\) .
Отношение \(~\displaystyle \frac{\gamma}{2 \alpha \beta} \approx 130~ ~\) имеет смысл времени, измеренного в днях, от начала проекта (\(x=0\)) до того момента, когда модель перестает быть применимой. Это ограничение допускает простую интерпретацию: либо печатный станок не успеет произвести количество денег, предусмотренное моделью, или даваемые Аллахом деньги не поместятся в здание местного банка, контролируемого мафией, из-за обесценивания этих денег, или чиновники, понимают, что после краха финансовой системы, их могут пригласить на казнь, и чуть уменьшают свои аппетиты.
Таким образом, несложная модель всего с несколькими параметрами демонстрирует прекрасно согласие с экспериментом, по крайней мере для положительных значений \(x\), когда стоимость рубля уже вышла на асимптотику, определяемую функцией Root и показанную на рисунке 2 тонкой черной кривой.
Предлагаемая выше модель имеет ограниченную область применимости; она не ухватывает начальный период процесса для значений времени \(-250<x<-10~\), то есть примерно с начала российского вооруженного вторжения в Украину до того момента, когда влияние этого вторжения на экономику России стало возможно описать простой моделью и несложнными элементарными функциями. Учет начала и конца главного периода экспроприации собственности на оккупированных территориях [6] может объяснять широкий максимум функции Arc, который не ухватывается функцией Root.
Conclusion
В области применимости этой модели, получаемая теоретическая функция Root находится в хорошем согласии как с предложенной ранее аппроксимацией Arc, так и с экспериментальными данными. Это согласие существенно лучше, чем согласие с экспериментальными данными оценок, прогнозов и предсказаний "стабилизации" рубля, сделанных на основе иных моделей и доступных в публикациях [7][8][9][10][11][12][13].
Аналогичные прогнозы стабилизации предлагаются также для значений времени \(x>100\), для которых экспериментальные данные пока недоступны. [14].
В начале 2015 года, стабильность, декларируемая многими авторами, проявляется в том, что в течение примерно года курс рубля стабильно, многократно пересекает аппроксимацию Arc. В частности, хорошее согласие с экспериментом имеет место для времен \(x>32\), то есть после того, как эта аппроксимация была предложена. На момент загрузки первой версии этой статьи, аппроксимация держится уже в течение 50 дней, несмотря на относительно слабые квазипериодичные компоненты с периодами порядка двух недель и месяца, видные на рисунке 3. Для \(x>0\), наблюдается также хорошее согласие экспериментальных данных с теоретической кривой Root.
Будет интересно сравнить будущие данные с предсказаниями линейной аппроксимации (рисунок 1), эллиптической аппроксимации (рисунки 1 и 2) с асимптотикой Sqrt из модели выше (рисунок 2) и с результатами других авторов [14]. Такое сравнение может быть предметом будущего исследования.
P.S.:
Примерно весной 2015 года, через месяц после публикации [15], предложенные выше аппроксимации достигают границы областей их применимости. С тех пор, по крайней мере до 2023 года, рубль болтается между одним и двумя американскими центами, хотя многие авторы отмечают сильную инфляцию. При этом, наблюдаются сообщения о том, что рост дотаций одной из республик РФ опережает инфляцию
[16][17][18][19][20].
Такие сообщения хорошо согласуется с моделью коллапсирующей экономики, представленной выше.
Можно ожидать, что распад РФ случится до того, как доля дотаций в пользу одной республики в бюджете России достигнет ста процентов. Анализ детальной информации о распределении бюджета РФ и собственности российских чиновников, если такая информация появится в открытом доступе, позволил бы использовать более детальные модели и предложить более определенные количественные оценки, в каком именно году ожидается распад российской экономической системы.
Reference
- ↑ http://mizugadro.mydns.jp/PAPERS/2015ARC/r02.pdf Дмитрий Кузнецов (Dmitrii Kouznetsov). Простая модель коллапсирующей экономики. 2015, in Russian. (The English version is expected to be loaded soon.)
- ↑ 2.0 2.1 2.2 https://www.mataf.net/en/currency/converter-USD-RUB
- ↑ 3.0 3.1 www.cbr.ru/scripts/XML_dynamic.asp?date_req1=01/01/2014&date_req2=01/05/2015&VAL_NM_RQ=R01235
- ↑ http://www.rg.ru/2008/10/01/korruptciya.html Владимир Кузьмин. Дмитрий Медведев провел первое заседание Совета по противодействию коррупции. 01.10.2008, 09:00.
- ↑ http://top.rbc.ru/society/05/10/2011/618868.shtml Р.Кадыров: Деньги Чечне дает Аллах. 05.10.2011, 17:35. Глава Чеченской Республики Рамзан Кадыров заявил 5 октября на встрече с журналистами, что деньги Чечне "дает Аллах".
- ↑ http://www.nytimes.com/2015/01/11/world/seizing-assets-in-crimea-from-shipyard-to-film-studio.html NEIL MacFARQUHAR. Seizing Assets in Crimea, From Shipyard to Film Studio. JAN. 10, 2015.
- ↑ http://top.rbc.ru/economics/29/09/2014/5429653dcbb20fc4e33ff87d Владислав Гордеев. Помощник президента предсказал волну укрепления рубля. 29.09.2014, 18:34. Помощник президента России Андрей Белоусов считает, что падение курса рубля не продлится долго, он назвал российскую валюту «переослабленной» и предсказал, что в будущем ее ждет «волна укрепления». Об этом, по информации Интерфакса, чиновник заявил в понедельник, 29 сентября.
- ↑ http://www.exocur.ru/analitiki-ozhidayut-ukrepleniya-rossiyskoy-valyutyi-po-itogam-oktyabrya/ Аналитики ожидают укрепления российской валюты по итогам октября. Новости 6 октября 2014.
- ↑ 2014.10.10. http://www.aif.ru/money/economy/1358024 Елена Трегубова. Когда стабилизируется рубль? Прогнозы экспертов. 18:19 10/10/2014.
- ↑ 2014.10.17. http://www.interfax-russia.ru/Ural/comment.asp?id=550539 Большинство уральских аналитиков к ноябрю ожидают ослабления рубля к доллару и укрепления - к евро 17.10.14 14:07.
- ↑ 2014.11.10. http://www.vestifinance.ru/articles/49157 Рубль стабилизируется. Каковы перспективы? 10.11.2014 12:29
- ↑ 2014.12.23. http://ria.ru/economy/20141223/1039848717.html Дмитрий Майоров. Рубль стабилизируется после 50-процентного роста за неделю. 20:06 23.12.2014.
- ↑ 2014.12.26. http://ria.ru/economy/20141226/1040272446.html Рубль стабилизируется на фоне неопределенной динамики нефтяных цен. 13:11 26.12.2014.
- ↑ 14.0 14.1 http://lenta.ru/news/2015/01/14/udaeva/ Юдаева спрогнозировала стабилизацию курса рубля с весны. 18:14, 14 января 2015.
- ↑ http://www.m-hikari.com/ams/ams-2015/ams-17-20-2015/kouznetsovAMS17-20-2015.pdf D.Kouznetsov. Currency band and the approximations: Fitting of rouble with 3-parametric functions. Applied Mathematical Sciences, Vol. 9, 2015, no. 17, 831 - 838 // Received: January 11, 2015; Published: January 29, 2015
- ↑ 2022.01.04. https://www.gazeta.ru/social/2022/01/24/14455081.shtml Анна Громова. «Без России мы не сможем». Кадыров раскрыл, сколько денег Чечня получает от Москвы Кадыров заявил, что на месте президента России уже «забрал бы Украину». 4 января 2022, 23:07 Общество. // Глава Чечни Рамзан Кадыров заявил, что без помощи федерального центра его регион не продержится и месяца. .. Кадыров отметил, что сейчас у региона нет собственного большого дохода, потому что он не занимается нефтедобычей. Чечня, по его словам, готова добывать нефть и строить нефтеперерабатывающие заводы, однако не может найти инвесторов. // «Нет [сегодня] этого всего. Нет у нас ни газа, ни света, ни нефти. <...> Я ищу уже семь лет, но не могу найти ни одного инвестора, чтобы занимался нефтедобычей, переработкой. Без России мы никак не сможем. <...> Если нам что-то другое предлагают, пусть напишут нам экономическую модель, как они хотят содержать республику», — заявил Кадыров. // Он добавил, что раньше сам поддерживал независимость региона и его отделение от России. Однако сейчас понимает, насколько республика нуждается в федеральной поддержке. // «Я тоже думал, что нужна нам независимая Ичкерия <...>. Но, клянусь, мы не сможем продержаться и трех месяцев [без помощи России]. Даже месяц не сможем <...>. Представьте, Россия за год на республику, на содержание народа Чеченской Республики 300 млрд тратит», — уточнил Кадыров.
- ↑ 2022.01.24. https://www.mk.ru/politics/2022/01/24/kadyrov-rossiya-tratit-na-soderzhanie-respubliki-300-mlrd-rubley-v-god.html 24.01.2022 в 17:03. Кадыров: Россия тратит на содержание республики 300 млрд рублей в год.
- ↑ 2022.01.24. https://www.gazeta.ru/politics/news/2022/01/24/17187487.shtml Альфия Мясумова. 24 января 2022, 20:40 «Думаю, что больше 300 млрд»: депутат Госдумы оценил слова Кадырова о тратах России на Чечню. // Член комитета Госдумы по бюджету и налогам Евгений Федоров в беседе с «Газетой.Ru» прокомментировал высказывание главы Чечни Рамзана Кадырова о том, что ежегодно Россия тратит 300 млрд рублей на содержание республики. Депутат считает, что на помощь региону уходит больше денежных средств. ..
- ↑ 2022.01.24. https://www.bbc.com/russian/news-60117012 Кадыров рассказал о 300 млрд рублей на содержание Чечни. Ошибся на порядок? 24 января 2022. Уровень дотационности Чечни по постоянию на январь-ноябрь 2021 года экономист Наталья Зубаревич оценивала в 84%. За этот период, говорила она в эфире радио "Эхо Москвы", другим регионам суммарно сократили трансферты на 6%, а Чечне увеличили на 13%.
- ↑ 2022.01.26. https://tass.ru/obschestvo/13522881 26 янв, 01:27 Кадыров пояснил свои слова о 375 млрд рублей, выделяемых из госбюджета на содержание Чечни // По словам главы республики, в эту сумму входит содержание на территории региона всех ветвей власти, филиалов федеральных органов и фондов, и эту цифру нельзя назвать "космической" // ГРОЗНЫЙ, 25 января. /ТАСС/. Сумма 375 млрд рублей в год, которую Чечня получает из госбюджета, включает в себя содержание всех ветвей власти, филиалов федеральных органов и фондов на территории республики, она сопоставима с суммами в других регионах и не является "космической". Об этом написал глава Чечни Рамзан Кадыров в своем Telegram-канале, комментируя озвученные в прямом эфире суммы на содержание региона. // Ранее в прямом эфире Кадыров сообщил, что на содержание Чечни ежегодно направляется более 300 млрд рублей из федерального бюджета, без этих денег регион не продержится и "трех месяцев". // "Речь о 375 млрд рублей. ..", - написал Кадыров. ..
http://lib.misto.kiev.ua/SHEKLY/r_weter.txt РОБЕРТ ШЕКЛИ. ПОДНИМАЕТСЯ ВЕТЕР. Перевод Э. Кобалевской. ..- Он говорит, настоящий ветер только начинается.
2022.01.29. https://www.anekdot.ru/id/1290767/
Наш мир стал другим. Если раньше в угрожаемый период население активно скупало соль, мыло и спички, то сейчас - денежные знаки вероятного противника.
Keywords
«Approximations of ruble», «Corruption», «Designate Russia as state sponsor of terrorism», «Inflation», «Linear approximation», «Nam krysh», «Pahanat», «Rouble», «Ruble», «Russia», «Russian invasion into Ukraine», «Sanctions» «Stop Putin»,
«Аппроксимация», «Вертикаль власти», «Денег нет», «Деньги Чечне даёт Аллах», «Линейная аппроксимация», «Коррупция», «Инфляция», «Нам крыш», «Паханат», «Предсказания революций», «Россия», «Распад РФ», «Революция», «Российское вторжение в Украину», «Рубль», «Санкции», «[[]]»,