Advection in log coordinate
Advection in log coordinate refers to the specific consideration of advection, using the change of independent variable in the advection equation
\((1) ~ ~ ~ \dot F(r,t)= - V'(r) F(r,t) - V(r) F'(r,t)\)
where \(r\) has sense of the independent coordinate, for example, size of particles;
\(t\) has sense of time;
\(V(r)\) determines the velocity, speed, rate of advection at coordinate \(r\) and is assumed to be a given function,
\(F(r,t)\) is unknown function, that is supposed to be found as solution of equation (1), assuming some additional condition(s); for example \(F(r,0)=F_0(r)\), where \(F_0\) is given function.
Here and through TORI, by default, the prime after the name of function indicates its derivative with respect to its first argument, and dot above the name of the function indicates its derivative with respect to the last argument.
This article considers the special case of transformation of the independent variable, namely, change from variable \(r\) to variable \(x=\ln(r)\) in such a way that \(r=\exp(x)\).
In order to write equation of advection in new coordinate, let
\((2) ~ ~ ~ \rho(x,t)=F(\mathrm e^x,t)~ \mathrm e^x\)
The goal of this article is to write out the equation for function \(\rho\), that follows from equation (1). It is desirable, however to have the resulting equation, that also can be interpreted as advection in the new coordinate.
Deduction
From equation (2), the distribution \(F\) can be expressed through the new function \(\rho\) as follows:
\((3) ~ ~ ~ \displaystyle F(r,t)=\frac{1}{r} \rho\Big(\ln(r),t\Big)\)
Then, its derivative with respect to its first argument, that appears in the right hand side of equation (1), can be written as follows:
\((4) ~ ~ ~ \displaystyle F'(r,t)= \frac{-1}{r^2} \rho\Big(\ln(r),t\Big) + \frac{1}{r}\rho\Big(\ln(r),t\Big) \frac{1}{r}\)
Change of variable \(r \mapsto \exp(x)\) gives
\((5) ~ ~ ~ \displaystyle F'(\mathrm e^x,t)= - \mathrm e ^{-2x} \rho(x,t)+\mathrm e^{-2x} \rho'(x,t)\)
With this expression, from equation (1), the derivative of \(\rho\) with respect to the last argument can be written as follows:
\((6) ~ ~ ~ \displaystyle \dot \rho(x,t)= \dot F(\mathrm e^x,t) ~ \mathrm e^x\) \(= \Big( - V'(\mathrm e^x)\, F(\mathrm e^x,t) -V(\mathrm e^x)\, F'(\mathrm e^x,t) \Big)~ \mathrm e^x\) \(=-V'(\mathrm e^x)\, F(\mathrm e^x,t)\,\mathrm e^x - V(\mathrm e^x)\,\mathrm e^x\, F'(\mathrm e^x,t)\) \(= -V'(\mathrm e^x)\,\rho(x,t) - V(\mathrm e^x)\,\Big(- \mathrm e ^{-x} \rho(x,t)+\mathrm e^{-x} \rho'(x,t)\Big)\) \(= -\Big(V'(\mathrm e^x) - \mathrm e^{-x} V(\mathrm e^x)\Big)\, \rho(x) -V(\mathrm e^x)\, \mathrm e^{-x} \rho'(x,t)\)
In order to interpret equation (6) as the advection equation, we need to define a new function \(W\), that have sense of velocity of drift; let
\((7) ~ ~ ~ \displaystyle W(x)=V(\mathrm e^x) \, \mathrm e^{-x}\)
Then, its derivative
\((8) ~ ~ ~ \displaystyle W('x)=V'(\mathrm e^x) -V(\mathrm e^x)\, \mathrm e^{-x}\)
and this is coefficient at the first term in the right hand side of equation (6). With function \(W\), equation (6) can be rewritten as follows:
\((9) ~ ~ ~ \displaystyle \dot \rho(x,t)= W'(x)\, \rho(x,t) - W(x)\, \rho'(x,t) \)
This is also advection equation (without diffusion); and this article is loaded to TORI in order to simplify the search of the deduction of this equation. Equation (9) indicates, that \(W(x)\) can be interpreted as the drift rate at coordinate \(x\), while \(\rho(x,t)\) has sense of density of distribution of some quantity along this coordinate.
Lognormal distribution
Change of variable \(r \mapsto x=\ln(t)\) has sense in order to apply the Fourier methods for the advection with distribution similar to the lognormal distribution. This refers to the case, when the initial condition for \(\rho\) id Gaussian, for example,
\((10) ~ ~ ~ \displaystyle \rho(x,0)= \frac{1}{\sqrt{\pi}} \exp(-x^2)\)
This corresponds to the lognormal initial condition for the function \(F\). This can be seen from the deduction below. This deduction refers to \(t\!=\!0\), so, the last argument in the deduction is omitted. Let
\((11) ~ ~ ~ \rho(x)\, \mathrm dx = F(r)\, \mathrm d r= F(\mathrm e^x)\, \mathrm e^x\, \mathrm d x \)
Then
\((12) ~ ~ ~ \rho(x)=F(\mathrm e^x) \mathrm e^x\)
\((13) ~ ~ ~ \rho\big(\ln(r)\big)=F(r) r\)
\((14) ~ ~ ~ \displaystyle F(r)=\frac{1}{r} \rho\big(\ln(r)\Big)\)
For the Gaussian (10), one this gives the initial lognormal function
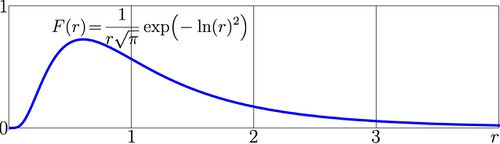
\((14) ~ ~ ~ \displaystyle F(r)=\frac{1}{r \sqrt{\pi}} \exp\Big(-\ln(r)^2\Big)\)
This function is shown in the Figure at right. Similar (a little bit more general) form of this lognormal distribution appears at Wikipedia, http://en.wikipedia.org/wiki/Log-normal_distribution
Discussion
Conclusion
Keywords
Advection, Derivative, Equation in partial derivatives, Exp, Log, Lognormal distribution
References
http://en.wikipedia.org/wiki/Log-normal_distribution
Deduction in this article is copied from Dima2014, page 115.