ArcCosqq

ArcCosqq is holomorphic function defined with

\(\text{acosqq}(z)=\text{acosq}(z)\, \tan\!\!\big( \text{acosq}(z) \big)\)

through functions acosq (or ArcCosq) expressed with

\(\text{acosq}(z)=\text{acosq}\big( \mathrm e ^{\mathrm i \pi /4}\, z \big)\)

which is ArcCosc of argument rotated for the phase quarter of \(\pi\). Namely this phase appears in the application for the atom optics, for channelling of particle between absorbing walls.

acosc or ArcCosc is inverse function of cosc,

\(\displaystyle \text{cosc}(z)=\frac{\cos(z)}{z}\)

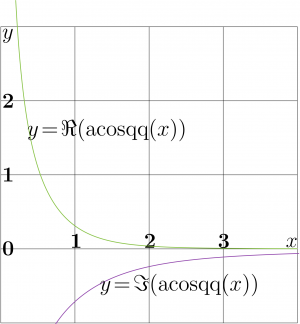
Graphic of the real part and that of the imaginary part of the function ArcCosqq of real argument are shown in the figure. While the argument approaches zero, functions ArcCosc and ArcCosq approach \(\pi/2\), and the Tangent in definition of ArcCosqq provides the singularity; so, the real part at zero becomes infinite.

Application

Function ArcCosqq expresses the decay of the atomic mode outside the channel, while function ArcCosq expresses the transversal wavenumber of this mode inside the channel. The argument of these functions has sense of the normalized damping of the atomic wave in the absorbing region.

Keywords

ArcCosc, Channeling of waves by absorbing walls, Makoto Morinaga