ArcTra
ArcTra is inverse of the Trappmann function; \(\mathrm{ArcTra}=\mathrm{tra}^{-1}\), where
(1)\(~ ~ ~ \mathrm{tra}(z)=z+\exp(z)\)
ArcTra can be expressed through the Tania function as follows:
(2) \(~ ~ ~ \mathrm{ArcTra}(z)=z-\mathrm{Tania}(z-1)\)
However the independent implementation of ArcTra can be arranged using its asymptotic properties.
Expansion at unity
\( \mathrm{ArcTra}(1+z)=\frac{z}{2}-\frac{z^2}{16}\) \( +\frac{z^3}{192}\) \( +\frac{z^4}{3072}\) \( -\frac{13 z^5}{61440}\) \( +\frac{47 z^6}{1474560}\) \( +\frac{73 z^7}{41287680}\) \( -\frac{2447 z^8}{1321205760}\) \( +\frac{16811 z^9}{47563407360}\) \( +\frac{15551 z^{10}}{1902536294400}\) \( -\frac{1726511 z^{11}}{83711596953600}\) \( +\frac{18994849 z^{12}}{4018156653772800}\) \( -\frac{10979677 z^{13}}{208944145996185600}\) \( -\frac{2983409137 z^{14}}{11700872175786393600}\) \( +\frac{48421103257 z^{15}}{702052330547183616000}\) \( -\frac{135002366063 z^{16}}{44931349155019751424000}\) \( -\frac{778870772857 z^{17}}{235025518657026392064000}\) \( +\frac{232033147779359 z^{18}}{219983885462976702971904000}\) \( -\frac{1305952009204319 z^{19}}{16718775295186229425864704000}\) \( -\frac{58740282660173759 z^{20}}{1337502023614898354069176320000}\) \( +\frac{1862057132555380307 z^{21}}{112350169983651461741810810880000}\) \( +O\left(z^{22}\right)\)
The approximation can written as follows:
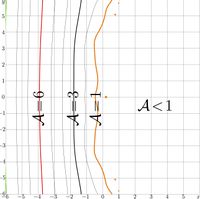
\(\displaystyle \mathrm{ArcTra}(z) \approx \mathrm{app1}(z) =\sum_{n=1}^M c_n (z-1)^n\)
This approximation returns at least 12 signifivant figures while \(|z-1|<1\). The precision can be characterised with the agreement
\(\displaystyle \mathcal A(z)= \) \(\displaystyle -\lg \left( \frac{ |\mathrm{tra}(\mathrm{app1}(z))-z| } { |\mathrm{tra}(\mathrm{app1}(z))| + |z|} \right)\)
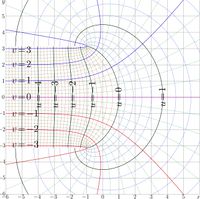
For \(M=21\), this agreement is shown in figure at right.
Expansion at \(-1-\mathrm i \pi\)
\( \mathrm{ArcTra}(z)=\) \( -\mathrm i \pi\) \( +\mathrm i \sqrt{2} \sqrt{z+\mathrm i \pi +1}\) \( +\frac{1}{3} (z+\mathrm i \pi +1)\) \( -\frac{\mathrm i (z+\mathrm i \pi +1)^{3/2}}{9 \sqrt{2}}\) \( -\frac{2}{135} (z+\mathrm i \pi +1)^2\) \( +\frac{\mathrm i (z+\mathrm i \pi +1)^{5/2}}{540 \sqrt{2}}\) \( -\frac{4 (z+\mathrm i \pi +1)^3}{8505}\) \( +\frac{139 \mathrm i (z+\mathrm i \pi +1)^{7/2}}{340200 \sqrt{2}}\) \( +\frac{2 (z+\mathrm i \pi +1)^4}{25515}\) \( -\frac{571 \mathrm i (z+\mathrm i \pi +1)^{9/2}}{73483200 \sqrt{2}}\) \( +\frac{1124 (z+\mathrm i \pi +1)^5}{189448875}\) \( +O\left((z+\mathrm i \pi +1)^{11/2}\right)\)
The same expansion van be written in more compact (and suitable for the implementation) form:
\( \mathrm{ArcTra}( -1 -\mathrm i \pi + 2 t^2)=\) \( -\mathrm i \pi\) \( +2 \mathrm i t\) \( +\frac{2 t^2}{3}\) \( -\frac{2 \mathrm i t^3}{9}\) \( -\frac{8 t^4}{135}\) \( +\frac{\mathrm i t^5}{135}\) \( -\frac{32 t^6}{8505}\) \( +\frac{139 \mathrm i t^7}{42525}\) \( +\frac{32 t^8}{25515}\) \( -\frac{571 \mathrm i t^9}{4592700}\) \( +\frac{35968 t^{10}}{189448875}\) \( + O(t^{11})\)
Expansion at \(-1+\mathrm i \pi\)
\( \mathrm{ArcTra}( -1 +\mathrm i \pi + 2 t^2)=\) \( \displaystyle \mathrm i \pi \) \(\displaystyle -2 \mathrm i t\) \(\displaystyle +\frac{2 t^2}{3}\) \(\displaystyle +\frac{2 \mathrm i t^3}{9}\) \(\displaystyle -\frac{8 t^4}{135}\) \(\displaystyle -\frac{\mathrm i t^5}{135}\) \(\displaystyle -\frac{32 t^6}{8505}\) \(\displaystyle -\frac{139 \mathrm i t^7}{42525}\) \(\displaystyle +\frac{32 t^8}{25515}\) \(\displaystyle +\frac{571 \mathrm i t^9}{4592700}\) \(\displaystyle +\frac{35968 t^{10}}{189448875}\) \(\displaystyle + O(t^{11})\)
The approximation with \(M\) terms can be written as follows:
\(\displaystyle \mathrm{ArcTra}(z)\approx \mathrm{app2}(z) \) \(\displaystyle = \) \(\displaystyle\sum_{n=1}^M c_n \left( \sqrt{\frac{z+1-\mathrm i \pi}{2}} \right)^n\)
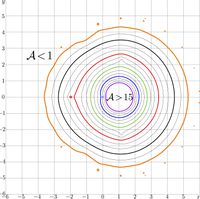
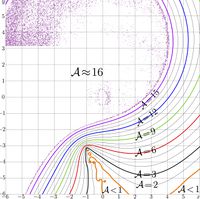
For \(m=10\), the agreement is shown in figure at right;
\(\displaystyle \mathcal A_2(z)= \) \(\displaystyle -\lg \left( \frac{ |\mathrm{tra}(\mathrm{app2}(z))-z| } { |\mathrm{tra}(\mathrm{app2}(z))| + |z|} \right)\)
The approximation \(\mathrm{app2}(z)\) reproduces one of the branch points of function ArcTra and corresponding cut line \(\Re(z)\le -1\), \(\Im(z)=\pi\).
Expansions at infinity, logarithmic growth
\(\mathrm{ArcTra}(z)=\) \(L\,\left( 1 +\frac{-1}{z} +\frac{1-L/2}{z^2} +\frac{-1+3 L/2 -L^2/3}{z^3} +\frac{1-3L+11L^2/6-L^3/4}{z^4} +\frac{-1+5L-35L^2/6+25L^3/12-L^4/5}{z^5} \right)\) \(+O(L/z)^5\)
where \(L=\ln(z)\). The expansion is valid fof \(z\in \mathbb C \) \(\backslash (\mathrm{strip} \cup \partial\, \mathrm{strip})\), where
\(\mathrm{strip}= \{ z \in \mathbb C: \Re(z)\!<\!0, |\Im(z)|<\pi \}\).
This expansion indicates the primary approximation
\(\mathrm{ArcTra}(z)\approx \) \(\mathrm{app3}(z)=\) \( \displaystyle \ln(z) \left(1+ \frac{1}{z} \sum_{m=0}^M \frac{P_m(\ln(z))}{z^m}\right)\)
where \(P_m\) is polynomial of \(m\)th order. In particular,
\(P_0(L)=-1\)
\(P_1(L)=1-L/2\)
\(P_2(L)=-1+3 L/2 -L^2/3\)
\(P_3(L)=1-3L+11L^2/6-L^3/4\)
\(P_4(L)=-1+5L-35L^2/6+25L^3/12-L^4/5\)
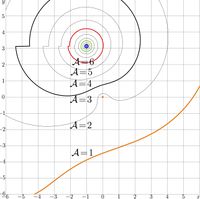
For \(M=4\), the agreement is shown in the picture;
\(\displaystyle \mathcal A_3(z)= \) \(\displaystyle -\lg \left( \frac{ |\mathrm{tra}(\mathrm{app3}(z))-z| } { |\mathrm{tra}(\mathrm{app3}(z))| + |z|} \right)\)
While \(|z|<5\), the primary approximation app3 provides at least 2 correct signifivant figures; however, it is assumed that \(\Re(z)\!>\!0\) \(\Cup\) \(|\Im(x)| \!>\!\pi\).
The primary approximation for \(\Re(z)\!<\!0\) , \(|\Im(x)| \!<\!\pi\) is considered in the next section.
Expansions at infinity, linear asumptotics
For the strip
\(\mathrm{strip}= \{ z \in \mathbb C: \Re(z)\!<\!0, |\Im(z)|<\pi \}\), there is special expansion:
\(\mathrm{ArcTra}(z)=\) \( z-\mathrm e^z\) \( +\mathrm e^{2z}\) \( -\frac{1}{2}\mathrm e^{3z}\) \( + O(\mathrm e^{4z})\)
\(\mathrm{app4}(z)=z-\mathrm e^z\) \( +\mathrm e^{2z}\) \( -\frac{1}{2}\mathrm e^{3z}\)
\(\displaystyle \mathcal A_4(z)= \) \(\displaystyle -\lg \left( \frac{ |\mathrm{tra}(\mathrm{app4}(z))-z| } { |\mathrm{tra}(\mathrm{app4}(z))| + |z|} \right)\)
Cutlines
Together, the expansions above cover with primary approximations all the complex plane \(z=z+\mathrm i y\) except two halflines
\(x\! \le \! -1\) , \(|y|\!=\!\pi\)
The precise numerical implementation of function ArcTra can be arranged adjusting the primary approximations, using the Newton method of adjusting of approximation of solution of algebraic equation with differentiable functions:
\(\displaystyle g_{n+1}(z)=g_n(z)+ \frac{ z-\mathrm{tra}(g_n(z))}{\mathrm{tra}^{\prime}(g_n(z))} \)
where \(g_0\) is one of the truncated series of the previous sections;
\( \mathrm{tra}^{\prime}(z) =1+\mathrm e^z \)
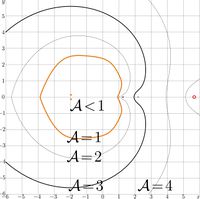
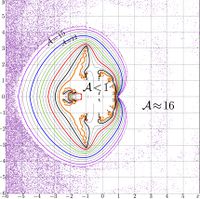
The agreement functions for the primary approximations app1, app2, app3, app4 described above and followed 3 adjustments with the Newton method are shown in the pictures below:
Let arctra1, arctra2, arctra3, arctra4 be routines implement the app1, app2, app3, app4, above together with 3 adjustments by the Newton method; then simple (although, perhaps, not optimal) choice of the approximation can be expressed with the following code:
z_type arctran(z_type z) { DB x=Re(z), y=Im(z);
if( x>2.) return arctra3(z);
DB Y=fabs(y);
if(Y<M_PI){ if(x<-1.5) return arctra4(z);
if(Y<2.) return arctra1(z); }
if( Y>5. || x<-4. ) return arctra3(z);
if( y>0. ) return arctra2(z);
return conj( arctra2(conj(z)) );
}
where DB means double and z_type means complex double. This implementation seems to provide at least 15 significant figures; it is best precision that can be achieved with complex double variables.
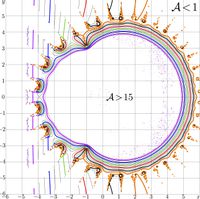
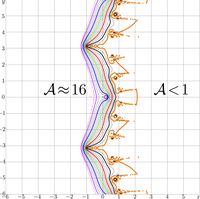
The choice of the primary approximation \(g_0\), dependently on the argument, determines the position of cut lines. They are chosen as continuation of the cut lines of functions
\(z \rightarrow \mathrm{app2}(z)~\) and
\(z \rightarrow \mathrm{app2}(z^*)^*\)
These cut lines are shown in the upper figure.
Application of ArcTra
The careful numerical implementation of function ArcTra described above have several goals.
The variety of expansions, that appear to be useful in the theory of superfunctions, seem to be not described in the literature. On the other hand, the strange expansions with inverse powers and logarithm, are not specific for superfunction, and function ArcTra is good example to practice in the implementation. It shows some feature, that appear with superfunctions, but easier to evaluate.
The function SuTra is interesting example of entire function with logarithmic asymptotic; it is superfunction of the Trappmann function tra\((z)=z+\mathrm e^z\). The inverse function AuTra, id est, the Abel function for Trappmann function, requires the ArcTra. For some values of the argument evaluation of AuTra requires several evaluations of function ArcTra. In order to perform the numerical check of the conjectures about AuTra, the efficient (fast, robust and precise) implementation of ArcTra is required.
In principle, the AuTra can be implemented through function AuZex, that is Abel function of \(\mathrm{zex}(z)=z \exp(z)\). However, the direct implementation through its asymptotic expansion and function ArcTra seems to be simpler, faster, preciser and easier to explain to colleagues. In such a way, function ArcTra provides the short way of construction, implementation and description of function AuTra.
The efficient implementation of function ArcTra, as the efficient implementations of SuTra, AuTra and and other superfunctions and Abel functions greatly extend the arsenal of functions, available for the description of non-trivial physical processes.