Lof

\(y\!=\)Factorial\((x)\) and \(y\!=\)Lof\((x)\)

\(u\!+\!\mathrm i v=\mathrm{Lof}(x\!+\!\mathrm i y)\)

Lof (or lof) is analytic extension of function \(~z\! \mapsto\! \ln\!\big(\)Factorial\((z)\big)~\) , that is holomorphic in the most of the complex \(z\) plane (except \(z\!\le\!-1\)).

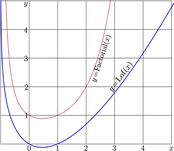
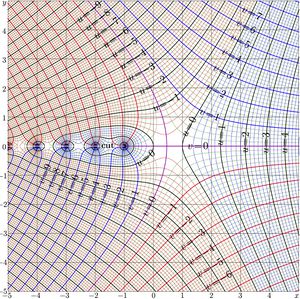
Complex map of function lof is shown in figure at right with lines \(u\!+\!\mathrm i v=\mathrm{Lof}(x\!+\!\mathrm i y)\) in the \(x\),\(y\) plane.

Terminology and apology

Name Lof is created from the beginning of names Logarithm and Factorial. In vicinity of positive part of the real axis, (for moderate imaginary part of the argument, it is, indeed, just combination of these two functions.

Properties of function Lof

Properties of function Lof follow from those of Factorial.

While the real part of the argument \(z\) dominates,

\(\mathrm{Lof}(z) = \) \(\displaystyle \ln\!\left( \int_0^\infty t^z \exp(-t)\, \mathrm{d}t \right)\)

For other values of the argument, appropriate integer factor of \(2\pi\mathrm i\) should be added to the right hand side of the integral representation in order to get the correct branch of Lof.

The correct branch can be achieved with formula of translation

\(\mathrm{Lof}(x\!+\!1)=\mathrm{Lof}(x)+\ln(x)\)

Behaviour of Factorial at large positive part of the argument (Stirling formula) Determines the asymptotic expansion

\(\displaystyle \mathrm{Lof}(x) \approx \) \(\displaystyle \big(\ln(x)-1\big) x\) \(\displaystyle +\frac{\ln(2\pi x)}{2}\) \(\displaystyle +\frac{1}{12 x}\) \(\displaystyle -\frac{1}{360 x^3}\) \(\displaystyle +\frac{1}{1260 x^5}\) \(\displaystyle -\frac{1}{1680 x^7}\) \(\displaystyle +O\!\left(\frac{1}{x^{9}}\right)\)

Applications

Lof happened to be useful for the analysis and debugging of implementations of various functions.

Factorial and its iterates (including non-integer and even not real iterates) are implemented using function lof.

Lof happened to be useful for the analysis of the asymptotic behaviour of the Hermite Gauss modes, oscillator functions, and in particular, the Amplitude of oscillator function.

Keywords

Factorial, Hermite Gauss mode, Hermite number, Oscillator function,,