Natural pentation

\(y=\mathrm{pen}(x)\) and related functions.

\(u\!+\!\mathrm i v=\mathrm{pen}(x\!+\!\mathrm i y )\)

\(u\!+\!\mathrm i v=\mathrm{pen}(x\!+\!\mathrm i y )~ ~\), zoomin

Natural pentation is pentation to base \(\mathrm e\!=\!\exp(1)\!\approx\!2.71\); it is holomorpic function in the range that includes the real axis.

Natural pentation is denoted with symbol pen; it is assumed that \(\mathrm{pen}=\mathrm{pen}_\mathrm e\).

Natural pentation is firth asckermann to base e, id est, \(\mathrm{pen}=A_{\mathrm e,5}\)

Natural pentation is supefrunction of natural tetration tet; natural pentation satisfies the transfer equation

\(\mathrm{pen}(z\!+\!1)=\mathrm{tet}\Big(\mathrm{pen}(z) \Big)\)

In this equation, the tetration \(\mathrm{tet}\) appears as the transfer function.

In addition, it is assumed, that \(\mathrm {pen}(1)=\mathrm e\).

Uniqueness

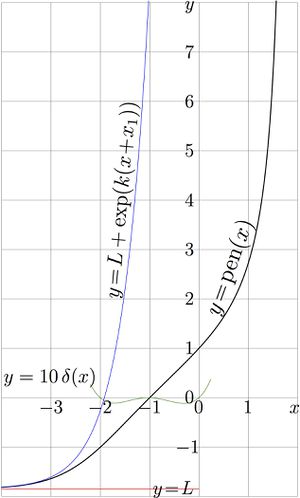
In order to provide the uniqueness, it is assumed, that pentation is constructed with the regular iteration at the lowest real fixed point of natural tetration, which is solution \(L=L_0\approx -1.8503545290271812\) of equation \(\mathrm{tet}(L)=L\). This level is shown in figure at right with red horizontal line.

Linear approximation

In vicinity of the real values of the argument, pentation can be approximated with linear function,

\(\mathrm{pen}(x) \approx 1+x\)

At \(-2.1<x<0.1\), this approximation provides at least 2 significant figures. Let \(\delta\) be he deviation,

\(\delta(x)=\mathrm{pen}(x)- (x+1)\)

In order to make this deviation visible, in the figure at right, graphic \(y\!=\! 10 \, \delta(x)\) is shown with thin green curve.

Asymptotic behavior and implementaiton

In order to make the solution of the transver equation unique, it is assumed the specific behavior of pentation at minus infinity,

\(\displaystyle \mathrm{pen}(z)= \sum_{m=0}^{M-1} \alpha_m \mathrm e^{mkz} + O(\mathrm e^{Mkz})\)

where \(k\approx 1.86573322821\) is real constant increment and \(\alpha\) are real constant coefficients;

\(\alpha_0 =L_0\approx −1.8503545290271812\)

It is convenenient to espress these coefficients as follows:

\(\displaystyle \alpha_m=\exp(m k x_1) a_m\)

where \(x_1\) is specific real constant, which is chosen in such a way, that the expansion can be written as follows:

\(\displaystyle \mathrm {tet}(z)=L_0 + \varepsilon + \sum_{m=2}^{M-1} a_m \varepsilon^m +O(\varepsilon^M)\)

where \(\varepsilon=\exp(k(x+x_1))\).

Then, \(a_1\) can be interpreted as unity.

Substitution of expanion into the transfer equation determines the coefficients \(a\); in particular,

\(a_2\approx -0.6263241\)

\(a_2 \approx 0.4827\)

For some fixed natural number \(M\!>\!1\), the primary approximation of superfunction \(f\) can be defined with

\(\displaystyle f(z)=L_0+\exp(kz)+\sum_{m=2}^{M-1} \exp(k z)\)

Then this approximation can be extended with

\(\displaystyle F_n(z)=\mathrm{tet}^n\Big( f(z\!-\!n)\Big)\)

Then, superfunction \(F\) appears as limit,

\(\displaystyle F(z)=\lim_{n\rightarrow \infty} F_n(z)=\lim_{n\rightarrow \infty} \mathrm{tet}^n f(z\!-\!n)\)

The pentation is expressed through this \(F\) as follows:

\(\mathrm{pen}(z)=F(x_1+z)\)

where \(x_1\) is solution of equation \(F(x_1)\!=\!1\).

This representation gives the straightforward way of evaluation of pentation. This procedure is just application of the general method of construction of superfunction with the regular iteration at the given fixed point \(L_0\) of the transfer function tet. As the numerical implementation of tetration is available, see fsexp.cin, the implementation of pentation does no bring serious problems; this representation is used to plot figures at the top. The primary approximation with \(M\!=\!1\) corresponds to the thin blue curve at the left side of the figure.

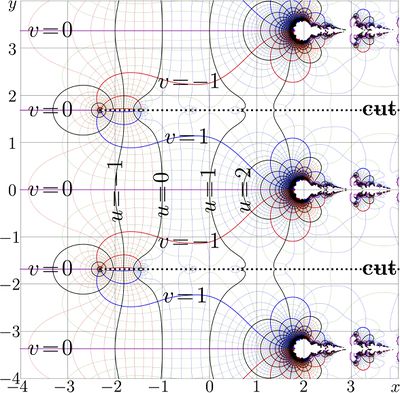
Periodicity and the cut lines

Pentation is periodic function, the period \(P\) is determined by the increment \(k\) above. This period is pure imaginary,

\(\displaystyle P= \frac{2\,\pi}{\mathrm i\, k} \approx 3.36767615657879 \, \mathrm i \)

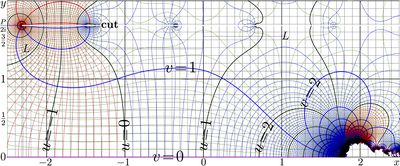
Correspondently, function pen has set of branchpoints and cutlines at the distance \(\pi/k\) from each other, parallel to the real axis. The cuts are directed along the real axis; it is not possible to rotate them to the left, because there is also countable set of singularities along each of these cut lines.

In addition, there are other branch points and the cut lines, displaced to unity from the solutions of equation \(\mathrm{pen}(z)=-2\) and from solutions of equations \(\mathrm{pen}(z)\le -2\). The last equation implies that \(\Im(\mathrm{pen}(z))=0\).

Fixed points of pentation and its superpentation

Natural pentation has set of fixed points, id est, solutions of equations \(L=\mathrm{pen}(L)\) Among others, from the map, one can measure "with finger" the following solutions:

\(L_{\mathrm e,5,1} \approx -2.260 \pm 1.384\, \mathrm i\)

\(L_{\mathrm e,5,3} \approx 1.057 \pm 1.546\, \mathrm i\)

These fixed points can be used to construct the superfunction of pentation, superpentation, and, in particular, the 6th Ackermann function, that can be called also hexation. The fixed points of pentation are complex, so, for the real–holomorphic superpentation, the method of the Cauchi integral can be applied, the same, used to construct and evaluate the natural tetration .

Perhaps, there exist at least two pretty different superpentations; one of them approaches \(L_{\mathrm e,5,1}\) and another approaches \(L_{\mathrm e,5,3}\) at \(\mathrm i \infty\). In such a way, the definition of the 6th ackermann may be not so straightforward as that of tetration and pentation; the appropriate choice of the asymptotic behaviour should be based on the intentional application. Up to year 2014, no application of pentation and hexation for physics is suggesed. Perhaps, the exp and tetration cover the needs of expression of fast growth in century 21, in the similar way, as the power function and exponential had covered these needs in centuries 18 and 19.

References

https://www.morebooks.de/store/ru/book/Суперфункции/isbn/978-3-659-56202-0
http://www.ils.uec.ac.jp/~dima/BOOK/202.pdf
http://mizugadro.mydns.jp/BOOK/202.pdf Д.Кузнецов. Суперфункции. Lambert Academic Publishing, 2014, In Russian.

http://www.ils.uec.ac.jp/~dima/PAPERS/2014acker.pdf
http://mizugadro.mydns.jp/PAPERS/2014acker.pdf D.Kouznetsov. Holomorphic ackermanns. 2014, under consideration

Keywords

Ackermann function, Holomorphic function, Natural tetration, Pentation, Superfunction, Tetration,