PGM

PGM is format of representation of the bitmap graphical information, oriented to the reading by the user-made programs.

The name is abbreviation of the portable Graymap Format

The standard extension of the PGM file is .pgm ; the PGM file can be created from the GIF file with the convert command:

Command line prompt> convert filename.gif filename.pgm

Syntaxis of the PGM file

The PGM file begins with the sequence of ascii characters that can b einterepreted as three lines.

The first line contains the two character word P5 .

Letter P indicates that the data are represented as pixmap.

Number 5 indicates that the fifth of the possible possible pixmaps is used. In general, there are more options; some of them are listed in table below:

first word	Type	Encoding
P1	Portable bitmap	ASCII
P2	Portable graymap	ASCII
P3	Portable pixmap	ASCII
P4	Portable bitmap	Binary
P5	Portable graymap	Binary
P6	Portable pixmap	Binary

(The ASCII based formats simplifies human-readability (and the most of operational systems, even "windows", recognize ascii);howeve, the binary formats are more efficient in the sense of speed of the reading by a user-written program and the size of the file.) The fifth option is used for the PGM files.

The Second line of the PGM file contains two natural in the decimal ascii. These numbers indicate size of the grid, at which the

Usage of PGM

The PGM can be used in the following scheme of storage and recovery of the graphical information. Some array calculated in the user-wtitten program can be stored as *.gif file:

Array in the user program \(\rightarrow\) EPSfile \(\rightarrow\) GIFfile

The GIF format allows the efficient compression of information. In addition, this format is recognized by the most of viewers, including the web browsers. Some of *.gif files are allowed and correctly interpreted by in the wiki sites, and, in particular, in TORI. (Id est, no special conversion should be specified to view the data stored.)

For the use in calculations, the *.gif files can converted to the PGM format, easy readable by the user-written programs.

Deal with the Bongard problem

Image p003 by

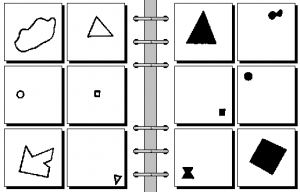
As the example of the use of the PGM, the initial stage of the algorithm for the solving of the Bongard problems is described here, namely, the the downloading of files and the extraction of the initial data from the original pictures .

Getting of files from the web

The pictures from the original site can be downloaded with the wget command

Command line prompt> <b> wget -r -np http://www.foundalis.com/res/bps/bpidx.htm </b>

Such a command makes the tree of directories which reproduces the structure original site and fills it with the content; in particular, all the *.gif figures of the Bongard problems are loaded.

The algorithm for the authomatic dealing with the huge numbers of pictures is not yet optimized and therefore not loaded. Below, the example of dealing with a single picture from the Third of the Bongard problems is described.

Below, it is assumed that the file www.foundalis.com/res/bps/bongard/p003.gif' is somehow copied or moved to p003.gif in the working directory.

Stripping of the pictures

First, the file should be converter to the PGM format:

Command line prompt> convert p003.gif p003.pgm

The resulting p003.pgm begins with

P5
516 330
255

The continunation is matrix of bytes, that vary from zero (hexagonal 00) to 255 (hexagonal FF) and represent the gray density that may have values from zero to 255.

The First picture of the Third Bongard problem

Such a file can be read with the C++ program; the file ado.cin also should be loaded to the working directory for the successful compilation of the code below; its output is shown in figure at right.

#include<math.h>
#include<stdio.h>
#include <stdlib.h>
using namespace std; 
#define DB double
#include "ado.cin"
#define DO(x,y) for(x=0;x<y;x++)
main(){ int j,k,K, m,M, n,N, u,U,v,V; DB s,t; 
char c1,c2,d;
FILE *i;
i=fopen("p003.pgm","r");
j=fscanf(i,"%c%c",&c1,&c2);    printf("%2d %c%c ",j,c1,c2);
j=fscanf(i,"%d%d%d",&M,&N,&K); printf("j=%2d M=%3d N=%3d K=%3d\n",j,M,N,K);
unsigned char  *a; a=(unsigned char *)malloc((size_t)((M*N)*sizeof(unsigned char)));
for(n=N-1; n>=0; n--){ //printf("%2d ",n);
	 DO(m,M) { j=fscanf(i,"%c",&d); a[M*n+m]=d;		}}
U=100; V=100;
FILE *o; o=fopen("fig1.eps","w"); ado(o, U+2, V+2);
fprintf(o,"1 1 translate\n");
unsigned char  *b; b=(unsigned char *)malloc((size_t)((U*V)*sizeof(unsigned char)));
//	DO(u,U) DO(v,V){ b[U*v+u]=a[M*(v+  9)+u+8];}  //fig3
//	DO(u,U) DO(v,V){ b[U*v+u]=a[M*(v+117)+u+8];}//fig2
	DO(u,U) DO(v,V){ b[U*v+u]=a[M*(v+225)+u+8];}//fig1
fprintf(o,"gsave\n");
fprintf(o,"%2d %2d scale\n",U,V);
fprintf(o,"%2d %2d 4 [%2d 0 0 %2d 0 %2d]\n<", U,V,U,-V,V);
s=0; DO(u,U)  DO(v,V){ t=0.+b[U*v+u]; if(t>s) s=t; }
s=15./s;
for(v=V-1;v>=0;v--) { fprintf(o,"\n");
DO(u,U){ fprintf(o,"%1x",int(s*b[U*v+u]+.6) );
     }}
fprintf(o,"\n>\n");
fprintf(o,"image\n");
free(a); free(b);
fprintf(o,"grestore\n");
fprintf(o,"showpage\n%c%cTrailer\n",'%','%'); fclose(o); 
system("epstopdf fig1.eps");
system(   "open fig1.pdf");
}

The program above reads the pictures of the Third Bongard problem in the PGM format, stores it in the array a. Then, it extracts the first picture as array b and writes it in the EPS format in the file fig1.eps .

Packing of the stripped pictures into the GIF format

From the methodological point of view, it is important that the program-solver "does not know" the origin of the files it deals with. Therefore, the extracted pictures should be stored in some portable format; the GIF is good choice, because it allows both: the viewing by a human and the easy conversion to the PGM format and reading by the Solver. This can be performed with the command

Command line prompt> convert fig1.eps fig1.gif

In such a GIF files, there is no extra information that could be used as a hint by a buggy (or on–honest) realization of the Bongard problem Solver. This is important to check the Axioms of TORI and verify that the algorithm of the Solver satisfies all the criteria of the Scientific knowledge.

The pictures stored in such a way can be used as the input files for the testing of the Bongard problem Solver. The solver converts each picture to the PGM format, reads it in a way, similar to that in the code above, but instead of writing the EPS file, the solver tries to determine, which class foes it belong to, and returns (or store) the answer.

The description of the solver of the Bongard problems falls out from the scope of the article about PGM and will be loaded as a separate article.

Postscriptum

In general, some of algorithms, suggested in TORI, for a narrow–profile specialist may look as an answer to the question

What scissors are better to use in order to hammer the screw into a wall?

If some specialists know, that instead of scissors, for the hammering, it is better to use the special instrument called hammer; or that in the case of a screw, the special tool called screw-driver is better than a scissors or a hammer, their comments and corrections should be greatly appreciated.