Difference between revisions of "Iterate of linear fraction"
(→Non-integer iterate: R->r) |
|||
| Line 70: | Line 70: | ||
(18) $~ ~ ~ \displaystyle v_n=\frac{1}{2} \left(r |
(18) $~ ~ ~ \displaystyle v_n=\frac{1}{2} \left(r |
||
| − | \left(\frac{2^{n+2}}{2^n-\left(-\frac{-2 |
+ | \left(\frac{2^{n+2}}{2^n-\left(-\frac{-2 r (v+w)+2 |
u+v^2+w^2}{u-v w}\right)^n}-2\right)+v-w\right)$ |
u+v^2+w^2}{u-v w}\right)^n}-2\right)+v-w\right)$ |
||
(19) $~ ~ ~ \displaystyle w_n= |
(19) $~ ~ ~ \displaystyle w_n= |
||
\frac{1}{2} \left(r |
\frac{1}{2} \left(r |
||
| − | \left(\frac{2^{n+2}}{2^n-\left(\frac{-2 |
+ | \left(\frac{2^{n+2}}{2^n-\left(\frac{-2 r (v+w)+2 |
u+v^2+w^2}{v w-u}\right)^n}-2\right)-v+w\right) |
u+v^2+w^2}{v w-u}\right)^n}-2\right)-v+w\right) |
||
$ |
$ |
||
Revision as of 12:35, 19 August 2013
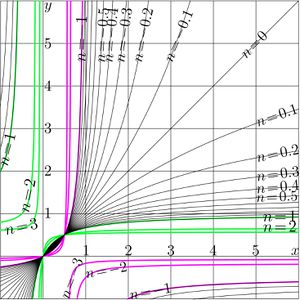
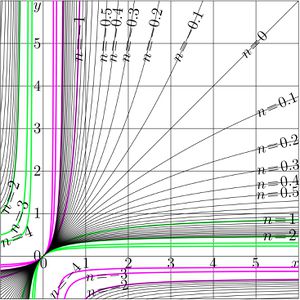
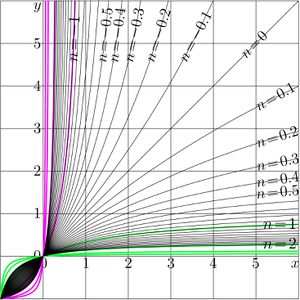
Iterate of linear fraction (or iteration of linnet friaciton) refers to function
(01)$~ ~ ~ \displaystyle T(z)=\frac{u+vz}{w+z}$
Iterate of a linear fraction can be expressed with also some linear fraction. This article describes this expression.
Special case
First, consider the special case when the iterated function has only single parameter. Let
(02) $~ ~ ~ \displaystyle t(z)=\frac{z}{c+z}$
where $c\ne 0$ is constant; for example, the real or complex number.
The iterate $t^n$ should satisfy the following equations:
$t^1(z)=t(z)$
$t^{m+n}(z)=t^m(t^n(z))$
For $c\ne 1$, the simple solution can be written as follows:
(03) $~ ~ ~ \displaystyle t^n(z)=\frac{z}{c^n+ \frac{1-c^n}{1-c} z }$
Limiting case
At $c=1$. The expression of the previous section cannot be applied as is. For this case, the $n$ th iteration of function $t(z)=\frac{z}{1+z}$ can be written as follows:
(04) $~ ~ ~ \displaystyle t^n(z)= $ $\displaystyle\lim_{c\rightarrow 1} $ $\displaystyle\frac{z}{c^n+ \frac{1-c^n}{1-c} z }=$ $\displaystyle\frac{z}{\displaystyle\lim_{s\rightarrow 0}\left( (1\!-\!s)^n + \frac{1-(1-s)^n}{s} z \right)}=$ $\displaystyle\frac{z}{1+nz}$
One can see that this expression satisfies equations
$ t^{n+1}(z)=t(t^n(z))=t^n(t(z))$
Generalization
Consider linear function $P$, let
(05) $~ ~ ~ \displaystyle P(z)=A + B z$
The inverse function can be written as follows:
(06) $~ ~ ~ \displaystyle Q(z)=P^{-1}(z)=\frac{x-A}{B}$
One can easy check that $P(Q(z))=Q(P(z))=z$. Let
(07) $~ ~ ~ \displaystyle T(z)=P(t(Q(z)))= \frac{ABc - AB - A^2 ~+~ (A\!+\!B)z}{Bc-A+z}$
This agree with equation (01) at
(08) $~ ~ ~ \displaystyle u=ABc-AB-A^2$ (09) $~ ~ ~ \displaystyle v=A+B$ (10) $~ ~ ~ \displaystyle w=Bc-A$
It is possible to express $A,B,c$ in terms of $u,v,w$:
(11) $~ ~ ~ \displaystyle A=\frac{v-w}{2} - r$
(12) $~ ~ ~ \displaystyle B=\frac{v+w}{2}+r$
(13) $~ ~ ~\displaystyle c=\frac{-2 u - v^2 - w^2 +(v+w) 2r}{2(u-vw)}$
where
(14) $~ ~ ~ \displaystyle r=\sqrt{u+\left(\frac{v-w}{2}\right)^2}$
In principle, it is possible to choose $R$ to be negative of the square root above. However, for the application in evaluation of the non-integer iterate, it is convenient to keep the coefficient $B$ positive, at least for positive $u,v,w$, in a wide range of their variation. In particular, the interpretation of transform $P$ is easier, while $P'(z)>0$.
Non-integer iterate
As function $g$ is expressed through conjugation of function $f$, the iteration can be expressed as follows:
(15) $~ ~ ~ \displaystyle T^n(z)=P(t^n(Q(z))$
All functions $P$, $t^n$ and $Q$ are defined above, and $f^n$ is expressed in a way, that does not require the number $n$ of iteration to be integer.
However, the $n$th iteration of function $T$ can be written also in a way, that explicitly shows that it is also linear fraction;
(16) $~ ~ ~ \displaystyle T^n(z)=\frac{u_n+v_n z}{w_n+z}$
Evaluation through equation ( 03), (15), (05),(06), and comparison to (01) give the coefficients:
(17) $~ ~ ~ \displaystyle u_n=u$
(18) $~ ~ ~ \displaystyle v_n=\frac{1}{2} \left(r
\left(\frac{2^{n+2}}{2^n-\left(-\frac{-2 r (v+w)+2
u+v^2+w^2}{u-v w}\right)^n}-2\right)+v-w\right)$
(19) $~ ~ ~ \displaystyle w_n= \frac{1}{2} \left(r
\left(\frac{2^{n+2}}{2^n-\left(\frac{-2 r (v+w)+2
u+v^2+w^2}{v w-u}\right)^n}-2\right)-v+w\right)
$
It looks strange, that $ u_n=u$, but the revision through Mathematica says, that it is really so.
In such a way, the linear fraction can be iterated any number of times, the halfiteration and the complex iterations are straightforward. In Mathematica, this could be expressed with the built-in function Nest, but, up to year 2013, the software does not yet allow to use it for non-integer number of iterate; if the number of iterations cannot be expressed with some positive integer constant, Mathematica generates the error message instead of to evaluate the expression.
Superfunction
The nth iteration of function $f$ can be used to express the superfunction for the linear fraction; if $f$ is declared as transfer function, then, for some constant $t$, the superfunciton $F$ can be written as follows:
$ F(z)=f^z(t)$
and the interse function $G=F^-1$ appears as the Abel function.
Linear fraction is one of transfer functions, for which the superfunction and the Abel function can be expressed in terms of elementary functions. For many cases, instead of to express the superfunction through the iterate of the transfer function, function, contrary, the iterate of the transfer function is experessed through the superfunction $F$ and the Abel function $G$ with
$f^n(z)=F(n+G(z))$
References
http://www.ams.org/journals/bull/1993-29-02/S0273-0979-1993-00432-4/S0273-0979-1993-00432-4.pdf Walter Bergweiler. Iteration of meromorphic functions. Bull. Amer. Math. Soc. 29 (1993), 151-188.
http://www.ams.org/mcom/2009-78-267/S0025-5718-09-02188-7/home.html
http://www.ils.uec.ac.jp/~dima/PAPERS/2009analuxpRepri.pdf
http://mizugadro.mydns.jp/PAPERS/2009analuxpRepri.pdf
D. Kouznetsov. Solution of F(x+1)=exp(F(x)) in complex z-plane. 78, (2009), 1647-1670
http://www.ils.uec.ac.jp.jp/~dima/PAPERS/2009vladie.pdf (English)
http://mizugadro.mydns.jp/PAPERS/2010vladie.pdf (English)
http://mizugadro.mydns.jp/PAPERS/2009vladir.pdf (Russian version)
D.Kouznetsov. Superexponential as special function. Vladikavkaz Mathematical Journal, 2010, v.12, issue 2, p.31-45.
http://reference.wolfram.com/mathematica/ref/Nest.html Nest, Wolfram Mathematica 9 Documentation center, 2013.