Difference between revisions of "ArcLambertW"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
| − | [[File:ArcLambertWplot.png|160px|thumb|Fig.1. |
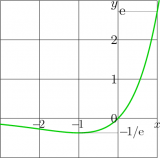
+ | [[File:ArcLambertWplot.png|160px|thumb|Fig.1. \(y\!=\!\mathrm{zex}(x)~\)]] |
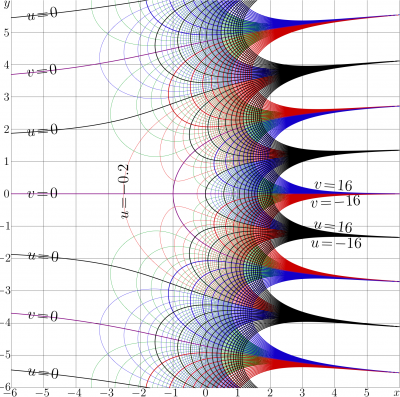
| − | [[File:ZexD6mapT100.png|400px|thumb|Fig.2. [[Complex map]], |
+ | [[File:ZexD6mapT100.png|400px|thumb|Fig.2. [[Complex map]], \(u\!+\!\mathrm i v\!=\!\mathrm{zex}(x\!+\!\mathrm i y)\)]] |
[[ArcLambertW]], called for simplicity '''zex''', is [[elementary function]] defined with |
[[ArcLambertW]], called for simplicity '''zex''', is [[elementary function]] defined with |
||
| − | (1) |
+ | (1) \(~ ~ ~ \mathrm{ArcLambertW}(z) = \mathrm{zex}(z) = z \exp(z) \) |
One of the inverse function of [[ArcLambertW]] is called [[LambertW]] |
One of the inverse function of [[ArcLambertW]] is called [[LambertW]] |
||
| Line 11: | Line 11: | ||
<ref>http://mathworld.wolfram.com/LambertW-Function.html |
<ref>http://mathworld.wolfram.com/LambertW-Function.html |
||
</ref>. |
</ref>. |
||
| − | In wide ranges of values of |
+ | In wide ranges of values of \(z\), the relations |
| − | (2) |
+ | (2) \(~ ~ ~ \mathrm{LambertW}\Big(\mathrm{zex}(z)\Big) = z \) |
and |
and |
||
| − | (3) |
+ | (3) \(~ ~ ~ \mathrm{zex}\Big(\mathrm{LambertW}(z)\Big) = z \) |
hold. |
hold. |
||
| − | For shortness, in expressions, name |
+ | For shortness, in expressions, name \(\mathrm{zex}\) is used instead of \(\mathrm {ArcLambertW}\). |
==[[SuZex]] and [[AuZex]]== |
==[[SuZex]] and [[AuZex]]== |
||
[[ArcLambertW]] can be treated as a [[transfer function]]. Its [[superfunction]] is denoted as [[SuZex]]. This function satisfies the [[transfer equation]] |
[[ArcLambertW]] can be treated as a [[transfer function]]. Its [[superfunction]] is denoted as [[SuZex]]. This function satisfies the [[transfer equation]] |
||
| − | (4) |
+ | (4) \(~ ~ ~ \mathrm{zex}\Big( \mathrm{SuZex}(z) \Big)=\mathrm{SuZex}(z\!+\!1)\) |
The complex map of [[SuZex]] is available in the category '''zex''' below. |
The complex map of [[SuZex]] is available in the category '''zex''' below. |
||
| − | The [[Abel function]] of [[ArcLambertW]] is named [[AuZex]]; |
+ | The [[Abel function]] of [[ArcLambertW]] is named [[AuZex]]; \(\mathrm{AuZex}=\mathrm{SuZex}^{-1}\). This function satisfies the [[Abel equation]] |
| − | (5) |
+ | (5) \(~ ~ ~ \mathrm{AuZex}\Big( \mathrm{zex}(z) \Big)=\mathrm{AuZex}(z)+1\) |
==Iterations of zex== |
==Iterations of zex== |
||
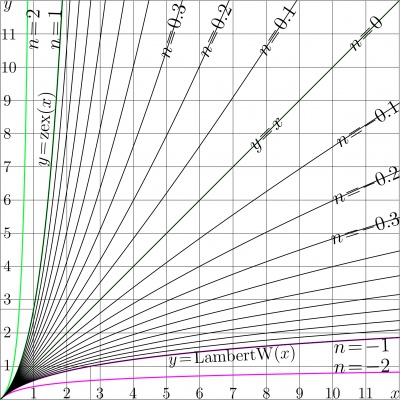
| − | [[File:ZexIteT.jpg|400px|thumb|Fig.3. Iterates |
+ | [[File:ZexIteT.jpg|400px|thumb|Fig.3. Iterates \(~y\!=\!\mathrm{zex}^n(x)~\) for various values of \(n\)]] |
With [[superfunction]] of [[zex]], called [[SuZex]], and the [[Abel function]], called [[AuZex]], the [[iterations]] of [[zex]] can be expressed as follows: |
With [[superfunction]] of [[zex]], called [[SuZex]], and the [[Abel function]], called [[AuZex]], the [[iterations]] of [[zex]] can be expressed as follows: |
||
| − | (8) |
+ | (8) \(~ ~ ~\mathrm{zex}^n(z)=\mathrm{SuZex}\Big( n+ \mathrm{AuZex}(z)\Big)\) |
| − | The number |
+ | The number \(n\) of iteration hax no need to be integer. For several real values of \(n\), the \(n\)th iteration of [[zex]] by (8) is plotted in figure at right, |
| − | (9) |
+ | (9) \(~ ~ ~y=\mathrm{zex}^c(x)\) |
| − | At |
+ | At \(n\!=\!2\), this gives \(y\!=\!\mathrm{zex}^2(x)\!=\!\mathrm{zex}\Big( \mathrm{zex}(x)\Big)\)<br> |
| − | at |
+ | at \(n\!=\!1\), this gives \(y\!=\!\mathrm{zex}(x)\!=\! x \exp(x)\)<br> |
| − | at |
+ | at \(n\!=\!0\), this gives identity function \(y\!=\!\mathrm{zex}^0(x)\!=\! x\)<br> |
| − | at |
+ | at \(n\!=\!-1\), this gives function \(y\!=\!\mathrm{zex}^{-1}(x)\!=\!\mathrm{LambertW}(x) ~ \), and so on. |
Figure 3 looks pretty similar to the plots of iterates of other functions with fast growth along the real axis. |
Figure 3 looks pretty similar to the plots of iterates of other functions with fast growth along the real axis. |
||
| Line 53: | Line 53: | ||
Expression (8) can be used for evaluation of funtion [[LambertW]]; however, such an evaluation is neither faster, nor preciser that that by the direct implementation of [[LambertW]] suggested in [[LambertW.cin]]. |
Expression (8) can be used for evaluation of funtion [[LambertW]]; however, such an evaluation is neither faster, nor preciser that that by the direct implementation of [[LambertW]] suggested in [[LambertW.cin]]. |
||
| − | The implementation of [[SuZex]] and [[AuZex]] is pretty similar to that of [[tetration]] to base |
+ | The implementation of [[SuZex]] and [[AuZex]] is pretty similar to that of [[tetration]] to base \(\exp^2(-1)\) |
<ref> |
<ref> |
||
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf |
http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf |
||
Latest revision as of 18:25, 30 July 2019
ArcLambertW, called for simplicity zex, is elementary function defined with
(1) \(~ ~ ~ \mathrm{ArcLambertW}(z) = \mathrm{zex}(z) = z \exp(z) \)
One of the inverse function of ArcLambertW is called LambertW [1][2] or also ProductLog [3]. In wide ranges of values of \(z\), the relations
(2) \(~ ~ ~ \mathrm{LambertW}\Big(\mathrm{zex}(z)\Big) = z \)
and
(3) \(~ ~ ~ \mathrm{zex}\Big(\mathrm{LambertW}(z)\Big) = z \)
hold.
For shortness, in expressions, name \(\mathrm{zex}\) is used instead of \(\mathrm {ArcLambertW}\).
SuZex and AuZex
ArcLambertW can be treated as a transfer function. Its superfunction is denoted as SuZex. This function satisfies the transfer equation
(4) \(~ ~ ~ \mathrm{zex}\Big( \mathrm{SuZex}(z) \Big)=\mathrm{SuZex}(z\!+\!1)\)
The complex map of SuZex is available in the category zex below.
The Abel function of ArcLambertW is named AuZex; \(\mathrm{AuZex}=\mathrm{SuZex}^{-1}\). This function satisfies the Abel equation
(5) \(~ ~ ~ \mathrm{AuZex}\Big( \mathrm{zex}(z) \Big)=\mathrm{AuZex}(z)+1\)
Iterations of zex
With superfunction of zex, called SuZex, and the Abel function, called AuZex, the iterations of zex can be expressed as follows:
(8) \(~ ~ ~\mathrm{zex}^n(z)=\mathrm{SuZex}\Big( n+ \mathrm{AuZex}(z)\Big)\)
The number \(n\) of iteration hax no need to be integer. For several real values of \(n\), the \(n\)th iteration of zex by (8) is plotted in figure at right,
(9) \(~ ~ ~y=\mathrm{zex}^c(x)\)
At \(n\!=\!2\), this gives \(y\!=\!\mathrm{zex}^2(x)\!=\!\mathrm{zex}\Big( \mathrm{zex}(x)\Big)\)
at \(n\!=\!1\), this gives \(y\!=\!\mathrm{zex}(x)\!=\! x \exp(x)\)
at \(n\!=\!0\), this gives identity function \(y\!=\!\mathrm{zex}^0(x)\!=\! x\)
at \(n\!=\!-1\), this gives function \(y\!=\!\mathrm{zex}^{-1}(x)\!=\!\mathrm{LambertW}(x) ~ \), and so on.
Figure 3 looks pretty similar to the plots of iterates of other functions with fast growth along the real axis.
Expression (8) can be used for evaluation of funtion LambertW; however, such an evaluation is neither faster, nor preciser that that by the direct implementation of LambertW suggested in LambertW.cin.
The implementation of SuZex and AuZex is pretty similar to that of tetration to base \(\exp^2(-1)\) [4].
Keywords
elementary function, Transfer function, LambertW, SuZex, AuZex, Inverse function
References
- ↑ http://en.wikipedia.org/wiki/Lambert_W_function
- ↑ http://www.maplesoft.com/support/help/Maple/view.aspx?path=LambertW
- ↑ http://mathworld.wolfram.com/LambertW-Function.html
- ↑ http://www.ams.org/journals/mcom/0000-000-00/S0025-5718-2012-02590-7/S0025-5718-2012-02590-7.pdf http://www.ils.uec.ac.jp/~dima/PAPERS/2011e1e.pdf H.Trappmann, D.Kouznetsov. Computation of the Two Regular Super-Exponentials to base exp(1/e). Mathematics of computation, 2012 February 8. ISSN 1088-6842(e) ISSN 0025-5718(p)