Difference between revisions of "Superpower"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
[[File:Superpower2plot.jpg|300px|thumb|Fig.1. Quadratic function (black curve) and two its superfunctions]] |
[[File:Superpower2plot.jpg|300px|thumb|Fig.1. Quadratic function (black curve) and two its superfunctions]] |
||
| − | [[Superpower]] or '''superpower function''' is [[superfunction]] for [[power function]] |
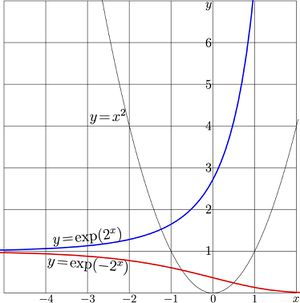
+ | [[Superpower]] or '''superpower function''' is [[superfunction]] for [[power function]] \(T(z)=z^a\) where \(a\) is parameter; often it is assumed, that \(a\!>\!1\). |
[[File:Superpower2map.jpg|300px|thumb|Fig.2. |
[[File:Superpower2map.jpg|300px|thumb|Fig.2. |
||
| − | + | \(u\!+\!\mathrm i v \!=\! \mathrm{SuPow}_2(x\!+\!\mathrm i y)\) ]] |
|
[[File:SdPow2map.jpg|300px|thumb|Fig.3. |
[[File:SdPow2map.jpg|300px|thumb|Fig.3. |
||
| − | + | \(u\!+\!\mathrm i v \!=\! \mathrm{SdPow}_2(x\!+\!\mathrm i y)\) ]] |
|
The two real-holomorphic superpower functions are considered here: |
The two real-holomorphic superpower functions are considered here: |
||
| − | + | \(\mathrm{SuPow}_a(z)=\exp(a^z)\) |
|
and |
and |
||
| − | + | \(\mathrm{SdPow}_a(z)=\exp(-a^z)\) |
|
| − | For |
+ | For \(a\!=\!2\), the explicit plots of these two functions are shown in figure 1 at right. |
==Transfer equation== |
==Transfer equation== |
||
| − | Functions [[SuPow]] and [[SdPow]] are solutions of the transfer equations for the superfunction |
+ | Functions [[SuPow]] and [[SdPow]] are solutions of the transfer equations for the superfunction \(F\) with function \(T\) as [[transfer function]], |
| − | + | \(F(z\!+\!1)=T(F(z))\) |
|
Finctions |
Finctions |
||
| − | + | \(F\!=\!\mathrm{SuPow}_a\) and |
|
| − | + | \(F\!=\!\mathrm{SdPow}_a\) and the modifications with displaced argument seems to be the only real-holomorphic solutions of the transfer equation with power function \(T\) as transfer function. |
|
==Periodicity== |
==Periodicity== |
||
| − | Complex map of function [[SuPow]] for the same value |
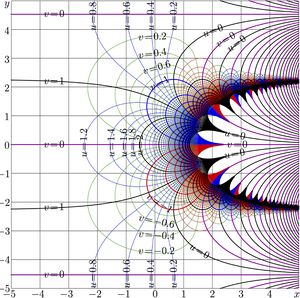
+ | Complex map of function [[SuPow]] for the same value \(a\!=\!2\) is shown in Figure 2. |
| − | Functions |
+ | Functions \(\mathrm{SuPow}_a\) and \(\mathrm{SdPow}_a\) are periodic; the period is |
| − | + | \(P= \mathrm i 2 \pi/\ln(a )\) |
|
| − | For positive |
+ | For positive \(a\), the period is pure imaginary. At \(a\!=\!2\), for the case shown in figure 2, the period |
| − | + | \(P=2\pi / \ln(2) \approx 9.06472028365\) |
|
| − | The map in Fig.2 is reproduced at the translations for, roughly, |
+ | The map in Fig.2 is reproduced at the translations for, roughly, \(~\pm 9.06472028365 ~\) |
along the Imaginary axis. The range of FIg.2 covers a little bit more that one period of the function. |
along the Imaginary axis. The range of FIg.2 covers a little bit more that one period of the function. |
||
| − | Functions |
+ | Functions \(\mathrm{SuPow}_a\) and \(\mathrm{SdPow}_a\) can be expressed through each other, |
| − | + | \(\mathrm{SdPow}_a(z)=\mathrm{SuPow}_a\big(z\!+\mathrm i \pi/\ln(a) \big)\) |
|
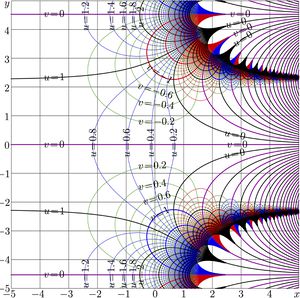
| − | In particular, map of function |
+ | In particular, map of function \(\mathrm{SdPow}_2\) shown in Fig.3, appears as displacement of map of \(\mathrm{SdPow}_2\), |
| − | shown in Fig.2, for |
+ | shown in Fig.2, for \(P/2\), id est, as translation for, roughly, 4.53236014183 along the imaginary axis. |
There is another relation between these two superfunctions: |
There is another relation between these two superfunctions: |
||
| − | + | \(\mathrm{SdPow}_a(z)=1/\mathrm{SuPow}_a(z)=\mathrm{SuPow}_a(z)^{-1}=\displaystyle\frac{1}{\mathrm{SuPow}_a(z)}\) |
|
==Inverse functions== |
==Inverse functions== |
||
[[File:Aupower2map.jpg|300px|thumb| |
[[File:Aupower2map.jpg|300px|thumb| |
||
| − | + | \(u\!+\!\mathrm i v\!=\!\mathrm{AuPow}_2(x\!+\!\mathrm i y)\)]] |
|
[[File:Adpow2map.jpg|300px|thumb| |
[[File:Adpow2map.jpg|300px|thumb| |
||
| − | + | \(u\!+\!\mathrm i v\!=\!\mathrm{AdPow}_2(x\!+\!\mathrm i y)\)]] |
|
Here, the inverse functions for superpower functions are denoted with [[AuPow]] and [[AdPow]]: |
Here, the inverse functions for superpower functions are denoted with [[AuPow]] and [[AdPow]]: |
||
| − | + | \(G=\mathrm{AuPow}_a=\mathrm{SuPow}_a^{-1}\) |
|
and |
and |
||
| − | + | \(G=\mathrm{AdPow}_a=\mathrm{SdPow}_a^{-1}\) |
|
These functions are [[Abel function]]s of the [[power function]] and they satisfy the [[Abel equation]]. |
These functions are [[Abel function]]s of the [[power function]] and they satisfy the [[Abel equation]]. |
||
| − | + | \(G(T(z))=G(z)+1\) |
|
| − | Solution |
+ | Solution \(G\) of this equation for \(~T(z)\!=\!z^a~\) can be referred as [[Abelpower]] function |
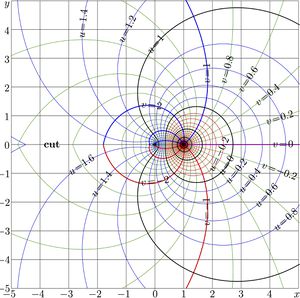
| − | For |
+ | For \(a\!=\!2\), [[complex map]] of function \(\mathrm{AuPow}_a\) is shown in figure at right. |
These functions differ for a constant, |
These functions differ for a constant, |
||
| − | + | \(\mathrm{AdPow}_a=\mathrm{AdPow}_a \pm P/2\) |
|
| − | where |
+ | where \(P\) is period of the [[superpower]] function defined above. Sign in this formula changes at the cut lines of functions |
| − | + | \(\mathrm{AuPow}_a\) and |
|
| − | + | \(\mathrm{AdPow}_a\); the sets of cut lines are different for these two functions. |
|
==Application of [[Superpower]]== |
==Application of [[Superpower]]== |
||
| Line 100: | Line 100: | ||
Terms [[power]] and [[superpower]] can be used also in a non-mathematical meaning. In this case, it does not denote a class of special (elementary) functions. |
Terms [[power]] and [[superpower]] can be used also in a non-mathematical meaning. In this case, it does not denote a class of special (elementary) functions. |
||
| − | In [[Physics]], term [[power]] denotes transfer of energy, refers to [[energy]] per [[time]] and can be measured in [[Watt]] |
+ | In [[Physics]], term [[power]] denotes transfer of energy, refers to [[energy]] per [[time]] and can be measured in [[Watt]]\(=\)[[Joule]]/[[second]]\(=\mathrm{ Kg\, m^2/sec^3}\). In this sense, [[power]] is main parameter of an engine, of an electric plant, of an electric cable, of a source of waves (highball mixer, laser, acoustic emitter, wave machine, etc.). |
Terms [[power]] and [[superpower]] may refer to big, enormous ability of some creature, subject, man or even countries. |
Terms [[power]] and [[superpower]] may refer to big, enormous ability of some creature, subject, man or even countries. |
||
| Line 126: | Line 126: | ||
==Keywords== |
==Keywords== |
||
[[Abelpower]], |
[[Abelpower]], |
||
| + | [[Iterate]], |
||
[[Power function]], |
[[Power function]], |
||
[[Superfunction]], |
[[Superfunction]], |
||
Latest revision as of 18:44, 30 July 2019
Superpower or superpower function is superfunction for power function \(T(z)=z^a\) where \(a\) is parameter; often it is assumed, that \(a\!>\!1\).
The two real-holomorphic superpower functions are considered here:
\(\mathrm{SuPow}_a(z)=\exp(a^z)\)
and
\(\mathrm{SdPow}_a(z)=\exp(-a^z)\)
For \(a\!=\!2\), the explicit plots of these two functions are shown in figure 1 at right.
Transfer equation
Functions SuPow and SdPow are solutions of the transfer equations for the superfunction \(F\) with function \(T\) as transfer function,
\(F(z\!+\!1)=T(F(z))\)
Finctions \(F\!=\!\mathrm{SuPow}_a\) and \(F\!=\!\mathrm{SdPow}_a\) and the modifications with displaced argument seems to be the only real-holomorphic solutions of the transfer equation with power function \(T\) as transfer function.
Periodicity
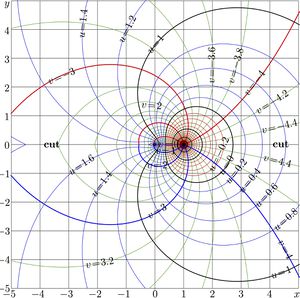
Complex map of function SuPow for the same value \(a\!=\!2\) is shown in Figure 2.
Functions \(\mathrm{SuPow}_a\) and \(\mathrm{SdPow}_a\) are periodic; the period is
\(P= \mathrm i 2 \pi/\ln(a )\)
For positive \(a\), the period is pure imaginary. At \(a\!=\!2\), for the case shown in figure 2, the period
\(P=2\pi / \ln(2) \approx 9.06472028365\)
The map in Fig.2 is reproduced at the translations for, roughly, \(~\pm 9.06472028365 ~\) along the Imaginary axis. The range of FIg.2 covers a little bit more that one period of the function.
Functions \(\mathrm{SuPow}_a\) and \(\mathrm{SdPow}_a\) can be expressed through each other,
\(\mathrm{SdPow}_a(z)=\mathrm{SuPow}_a\big(z\!+\mathrm i \pi/\ln(a) \big)\)
In particular, map of function \(\mathrm{SdPow}_2\) shown in Fig.3, appears as displacement of map of \(\mathrm{SdPow}_2\), shown in Fig.2, for \(P/2\), id est, as translation for, roughly, 4.53236014183 along the imaginary axis.
There is another relation between these two superfunctions:
\(\mathrm{SdPow}_a(z)=1/\mathrm{SuPow}_a(z)=\mathrm{SuPow}_a(z)^{-1}=\displaystyle\frac{1}{\mathrm{SuPow}_a(z)}\)
Inverse functions
Here, the inverse functions for superpower functions are denoted with AuPow and AdPow:
\(G=\mathrm{AuPow}_a=\mathrm{SuPow}_a^{-1}\)
and
\(G=\mathrm{AdPow}_a=\mathrm{SdPow}_a^{-1}\)
These functions are Abel functions of the power function and they satisfy the Abel equation.
\(G(T(z))=G(z)+1\)
Solution \(G\) of this equation for \(~T(z)\!=\!z^a~\) can be referred as Abelpower function
For \(a\!=\!2\), complex map of function \(\mathrm{AuPow}_a\) is shown in figure at right.
These functions differ for a constant,
\(\mathrm{AdPow}_a=\mathrm{AdPow}_a \pm P/2\)
where \(P\) is period of the superpower function defined above. Sign in this formula changes at the cut lines of functions \(\mathrm{AuPow}_a\) and \(\mathrm{AdPow}_a\); the sets of cut lines are different for these two functions.
Application of Superpower
Superpower function is important example to illustrate properties of superfunctions.
Other superfunctions mentioned in Table of superfunctions show properties, similar to those of functions SuPow and SdPow. This applies also to superfunctions, that cannot be expressed through the elementary functions.
Funcitons SuPow and SdPow, as they are elementary functions, are good to see, what can be expected from superfuncitons of other transfer function, more complicated than just a quadratic function.
It should be interesting to construct a proof, that for the power function, the SuPow and SdPow are the only non–trivial superfunctions with simple asymptotic behaviour, and other periodic superfunctions appear at the displacement of the argument for a constant.
Other meanings of term superpower
Terms power and superpower can be used also in a non-mathematical meaning. In this case, it does not denote a class of special (elementary) functions.
In Physics, term power denotes transfer of energy, refers to energy per time and can be measured in Watt\(=\)Joule/second\(=\mathrm{ Kg\, m^2/sec^3}\). In this sense, power is main parameter of an engine, of an electric plant, of an electric cable, of a source of waves (highball mixer, laser, acoustic emitter, wave machine, etc.).
Terms power and superpower may refer to big, enormous ability of some creature, subject, man or even countries.
In some context, words "power" and superpower are difficult to interpret in any of meanings mentioned above. [1]
For this reason, in TORI, the only meaning mentioned in the previous sections is supposed to used.
References
- ↑
http://www.dosguys.com/JCS/Jesus_Christ_Superstar_-_Chords_&_Lyrics_(by_RA).htm
JESUS CHRIST SUPERSTAR by Andrew Lloyd Webber & Tim Rice. 7/7/2007. 2-3 Poor Jerusalem:
Neither you Simon, nor the fifty thousand
Nor the Romans, nor the Jews,
Nor Judas, nor the Twelve, nor the Priests, nor the Scribes,
Nor doomed Jerusalem itself
Understand what power is ..
Keywords
Abelpower, Iterate, Power function, Superfunction, Superfunctions, SdPow, SuPow, Table of superfunctions