Difference between revisions of "File:Norifit76plot.jpg"

From TORI
Jump to navigation Jump to search
(Importing image file)
 
 
Line 1: Line 1:
  +
Analysis of the approximation of [[nori function]] through function [[korifit76]],
−
Importing image file
  
  +
  +
[[nori]]$(x)=\, $[[kori]]$(x)^2\approx\, $[[korifit76]]$(x)^2$
  +
  +
The free agreements are shown:
  +
  +
$\mathrm{agreeA}(x)= - \lg\! \Big( \big|\mathrm{korifit76}(x)^2-\mathrm{nori}(x)\big|\Big)$
  +
  +
$\mathrm{agreeB}(x)= - \lg\! \Big( \big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big| \Big)$
  +
  +
$\displaystyle
  +
\mathrm{agreeC}(x)= - \lg \left(\frac {\big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big|}{\big|\mathrm{korifit76}(x)\big| + \big|\mathrm{kori}(x)\big|}\,\right)$
  +
  +
where functions nori and kori are evaluated through the straightforward definitions using the [[C++]] built-in [[Bessel function]] double [[j0]](double ).
  +
  +
[[kori]]$(x) =\,$[[mori]]$\big(\sqrt{x}\big)$ $\,= \displaystyle \frac{ J_0\big(L_1 \sqrt{x} \big)}{1-x}$
  +
  +
where $L_n =\,$[[BesselJZero]]$[0,n]~$ is $n$th zero of function [[BesselJ0]].
  +
  +
For reference, at the bottom, functions [[nori]] and [[kori]], scaled with factor 10, are shown with green and red curves.
  +
  +
The additional vertical grid lines show abscissas
  +
$\displaystyle
  +
M_n=\left(\frac{L_n}{L_1}\right)^2~ $ for $~n=2\,..\,5$
  +
  +
==[[korifit76]]==
  +
  +
Function [[korifit76]] is defined in the following way:
  +
  +
$\mathrm{kori76fit}= \displaystyle
  +
\prod_{n=2}^7\! \left(1-\frac{L_1^2}{L_n^2}x\right)~ \frac{1+\sum_{n=1}^6 a_n x^n}{1+\sum_{n=1}^6 b_n x^n}
  +
$
  +
  +
where $L_n=\mathrm{BesselJZero}[0,n]$ and coefficients $a$ and $b$ are:
  +
  +
$\begin{array}{l}
  +
a_1=-0.04844698269548584 \\
  +
a_2= 0.0010028289633265202 \\
  +
a_3= -0.000011428855401098336\\
  +
a_4= 7.61813379974462\times 10^{-8}\\
  +
a_5= -2.8376606186641804\!\times\! 10^{-10}~\\
  +
a_6= 4.651275051439759\times 10^{-13}
  +
\end{array}$
  +
$\begin{array}{l}
  +
b_1= 0.03223483760044156\\
  +
b_2= 0.0004974915308429358\\
  +
b_3= 4.7768603073237505\times 10^{-6}\\
  +
b_4= 3.071615607112112\times 10^{-8}\\
  +
b_5= 1.292095753771865\times 10^{-10}\\
  +
b_6= 2.925186494186955\times 10^{-13}
  +
\end{array}
  +
$
  +
  +
==[[C++]] generator of curves==
  +
  +
<poem><nomathjax><nowiki>
  +
#include <stdio.h>
  +
#include <stdlib.h>
  +
#define DB double
  +
#define DO(x,y) for(x=0;x<y;x++)
  +
//using namespace std;
  +
#include <complex>
  +
typedef std::complex<double> z_type;
  +
#define Re(x) x.real()
  +
#define Im(x) x.imag()
  +
#define I z_type(0.,1.)
  +
#define M(x,y) fprintf(o,"%6.4lf %6.4lf M\n",0.+x,0.+y);
  +
#define L(x,y) fprintf(o,"%6.4lf %6.4lf L\n",0.+x,0.+y);
  +
  +
#include "korifit76.cin"
  +
#include "ado.cin"
  +
  +
DB L1=2.404825557695773;
  +
DB L2=5.5200781102863115;
  +
DB L3=8.653727912911013;
  +
DB L4=11.791534439014281;
  +
DB L5=14.930917708487787;
  +
DB L6=18.071063967910924;
  +
DB L7=21.21163662987926;
  +
DB L8=24.352471530749302;
  +
  +
DB LN[9]={ 0., 2.404825557695773, 5.5200781102863115,
  +
8.653727912911013,11.791534439014281,14.930917708487787,
  +
18.071063967910924,21.21163662987926, 24.352471530749302};
  +
  +
int main(){int m,n,i; double x,y,z,t,u; FILE *o;
  +
  +
o=fopen("norifit76plo.eps","w");
  +
ado(o,520,220);
  +
fprintf(o,"10 10 translate 10 10 scale 2 setlinecap 1 setlinejoin\n");
  +
  +
for(m=0;m<51;m+=1) {M(m,0)L(m,15)}
  +
for(n=0;n<16;n+=1){M(0,n)L(50,n)}
  +
fprintf(o,"0.04 W S\n");
  +
  +
for(m=2;m<6;m++){ x=LN[m]/LN[1]; x*=x; M(x,0)L(x,20) }
  +
fprintf(o,"0.03 W 1 0 1 RGB S\n");
  +
  +
for(n=1;n<5001;n+=5){ x=.01*n;
  +
y=j0(L1*sqrt(x))/(1.-x); y*=y;
  +
z=Re(korifit76(x)); z*=z;
  +
t=y-z;
  +
u=-log(fabs(t))/log(10);
  +
printf("%6.2lf %19.16lf %19.16lf %19.16lf %8.2lf\n",x,y,z,t,u);
  +
if(n==1) M(x,u) else if(u>0 && u <20)L(x,u)
  +
}
  +
fprintf(o,"0 .7 0 RGB .1 W S\n");
  +
  +
for(n=1;n<5001;n+=5){ x=.01*n;
  +
y=j0(L1*sqrt(x))/(1.-x);
  +
z=Re(korifit76(x));
  +
t=y-z;
  +
u=-log(fabs(t))/log(10);
  +
printf("%6.2lf %19.16lf %19.16lf %19.16lf %8.2lf\n",x,y,z,t,u);
  +
if(n==1) M(x,u) else if(u>0 && u <20)L(x,u)
  +
}
  +
fprintf(o,"1 0 0 RGB .1 W S\n");
  +
  +
for(n=1;n<5001;n+=5){ x=.01*n;
  +
y=j0(L1*sqrt(x))/(1.-x); y*=y;
  +
z=Re(korifit76(x)); z*=z;
  +
t=y-z;
  +
u=-log(fabs(t)/(fabs(y)+fabs(z)))/log(10);
  +
printf("%6.2lf %19.16lf %19.16lf %19.16lf %8.2lf\n",x,y,z,t,u);
  +
if(n==1) M(x,u) else if(u>0 && u <20)L(x,u)
  +
}
  +
fprintf(o,"0 0 0 RGB .1 W S\n");
  +
  +
for(n=1;n<5001;n+=5){ x=.01*n;
  +
y=j0(L1*sqrt(x))/(1.-x);
  +
if(n==1) M(x,10*y) else if(y>-1 && y <2)L(x,10*y) }
  +
fprintf(o,"1 0 0 RGB .1 W S\n");
  +
  +
for(n=1;n<5001;n+=5){ x=.01*n;
  +
y=j0(L1*sqrt(x))/(1.-x); y*=y;
  +
if(n==1) M(x,10*y) else if(y>-1 && y <2)L(x,10*y) }
  +
fprintf(o,"0 .6 0 RGB .1 W S\n");
  +
  +
fprintf(o,"showpage\n%c%cTrailer\n",'%','%'); fclose(o);
  +
system("epstopdf norifit76plo.eps");
  +
system( "open norifit76plo.pdf");
  +
return 0;}
  +
</nowiki></nomathjax></poem>
  +
  +
  +
==[[Latex]] generator of labels==
  +
  +
<poem><nomathjax><nowiki>
  +
\documentclass[12pt]{article}
  +
\usepackage{geometry}
  +
\usepackage{graphics}
  +
\usepackage{rotating}
  +
\paperwidth 516pt
  +
\paperheight 216pt
  +
\textwidth 420pt
  +
\textheight 300pt
  +
\topmargin -108pt
  +
\oddsidemargin -73pt
  +
\newcommand \ds {\displaystyle}
  +
\newcommand \sx {\scalebox}
  +
\newcommand \rme {\mathrm{e}}
  +
\newcommand \rot {\begin{rotate}}
  +
\newcommand \ero {\end{rotate}}
  +
\newcommand \ing {\includegraphics}
  +
\pagestyle{empty}
  +
\parindent 0pt
  +
\begin{document}
  +
%\begin{picture}(410,126)
  +
\begin{picture}(614,212)
  +
%\put(0,0){\ing{moriplo}}
  +
%\put(0,0){\ing{23}}
  +
%\put(0,0){\ing{korifit76plo}}
  +
\put(4,0){\ing{norifit76plo}}
  +
\put(6,200){\sx{1.1}{$y$}}
  +
\put(0,156){\sx{1.1}{$15$}}
  +
\put(0,106){\sx{1.1}{$10$}}
  +
\put(0, 56){\sx{1.1}{$~5$}}
  +
\put(0, 6){\sx{1.1}{$~0$}}
  +
\put(11,-1){\sx{1.1}{$0$}}
  +
%\put(43,-2){\sx{1.}{$(L_2/L_1)^2$}}
  +
\put(60,0){\sx{1.}{$M_2$}}
  +
\put(107,-1){\sx{1.1}{$10$}}
  +
\put(137,0){\sx{1.}{$M_3$}}
  +
%\put(159,-1){\sx{1.1}{$15$}}
  +
\put(208,-1){\sx{1.1}{$20$}}
  +
\put(248,0){\sx{1.}{$M_4$}}
  +
\put(309,-1){\sx{1.1}{$30$}}
  +
\put(393,0){\sx{1.}{$M_5$}}
  +
\put(410,-2){\sx{1.1}{$40$}}
  +
\put(509,-2){\sx{1.1}{$x$}}
  +
\put(24,82){\rot{-65}\sx{.9}{$y\!=\! 10\, \mathrm{kori}(x)$}\ero}
  +
\put(12,52){\rot{-65}\sx{.9}{$y\!=\! 10 \mathrm{nori}(x)$}\ero}
  +
%
  +
\put(440,162){\rot{-20}\sx{1.1}{$y\!=\! \mathrm{agreeA}(x)$}\ero}
  +
\put(432,132){\rot{-25}\sx{1.1}{$y\!=\! \mathrm{agreeB}(x)$}\ero}
  +
\put(426,110){\rot{-25}\sx{1.1}{$y\!=\! \mathrm{agreeC}(x)$}\ero}
  +
%\put(576,60){\rot{-16}\sx{1.3}{$y\!=\! 10 \mathrm{agreeC}(x)}(x)$}\ero}
  +
\end{picture}\end{document}
  +
</nowiki></nomathjax></poem>

Latest revision as of 08:44, 1 December 2018

Analysis of the approximation of nori function through function korifit76,

nori$(x)=\, $kori$(x)^2\approx\, $korifit76$(x)^2$

The free agreements are shown:

$\mathrm{agreeA}(x)= - \lg\! \Big( \big|\mathrm{korifit76}(x)^2-\mathrm{nori}(x)\big|\Big)$

$\mathrm{agreeB}(x)= - \lg\! \Big( \big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big| \Big)$

$\displaystyle \mathrm{agreeC}(x)= - \lg \left(\frac {\big|\mathrm{korifit76}(x)-\mathrm{kori}(x)\big|}{\big|\mathrm{korifit76}(x)\big| + \big|\mathrm{kori}(x)\big|}\,\right)$

where functions nori and kori are evaluated through the straightforward definitions using the C++ built-in Bessel function double j0(double ).

kori$(x) =\,$mori$\big(\sqrt{x}\big)$ $\,= \displaystyle \frac{ J_0\big(L_1 \sqrt{x} \big)}{1-x}$

where $L_n =\,$BesselJZero$[0,n]~$ is $n$th zero of function BesselJ0.

For reference, at the bottom, functions nori and kori, scaled with factor 10, are shown with green and red curves.

The additional vertical grid lines show abscissas $\displaystyle M_n=\left(\frac{L_n}{L_1}\right)^2~ $ for $~n=2\,..\,5$

korifit76

Function korifit76 is defined in the following way:

$\mathrm{kori76fit}= \displaystyle \prod_{n=2}^7\! \left(1-\frac{L_1^2}{L_n^2}x\right)~ \frac{1+\sum_{n=1}^6 a_n x^n}{1+\sum_{n=1}^6 b_n x^n} $

where $L_n=\mathrm{BesselJZero}[0,n]$ and coefficients $a$ and $b$ are:

$\begin{array}{l} a_1=-0.04844698269548584 \\ a_2= 0.0010028289633265202 \\ a_3= -0.000011428855401098336\\ a_4= 7.61813379974462\times 10^{-8}\\ a_5= -2.8376606186641804\!\times\! 10^{-10}~\\ a_6= 4.651275051439759\times 10^{-13} \end{array}$ $\begin{array}{l} b_1= 0.03223483760044156\\ b_2= 0.0004974915308429358\\ b_3= 4.7768603073237505\times 10^{-6}\\ b_4= 3.071615607112112\times 10^{-8}\\ b_5= 1.292095753771865\times 10^{-10}\\ b_6= 2.925186494186955\times 10^{-13} \end{array} $

C++ generator of curves


#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
//using namespace std;
#include <complex>
typedef std::complex<double> z_type;
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#define M(x,y) fprintf(o,"%6.4lf %6.4lf M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.4lf %6.4lf L\n",0.+x,0.+y);

#include "korifit76.cin"
#include "ado.cin"

DB L1=2.404825557695773;
DB L2=5.5200781102863115;
DB L3=8.653727912911013;
DB L4=11.791534439014281;
DB L5=14.930917708487787;
DB L6=18.071063967910924;
DB L7=21.21163662987926;
DB L8=24.352471530749302;

DB LN[9]={ 0., 2.404825557695773, 5.5200781102863115,
 8.653727912911013,11.791534439014281,14.930917708487787,
18.071063967910924,21.21163662987926, 24.352471530749302};

int main(){int m,n,i; double x,y,z,t,u; FILE *o;

o=fopen("norifit76plo.eps","w");
ado(o,520,220);
fprintf(o,"10 10 translate 10 10 scale 2 setlinecap 1 setlinejoin\n");

for(m=0;m<51;m+=1) {M(m,0)L(m,15)}
for(n=0;n<16;n+=1){M(0,n)L(50,n)}
fprintf(o,"0.04 W S\n");

for(m=2;m<6;m++){ x=LN[m]/LN[1]; x*=x; M(x,0)L(x,20) }
fprintf(o,"0.03 W 1 0 1 RGB S\n");

for(n=1;n<5001;n+=5){ x=.01*n;
        y=j0(L1*sqrt(x))/(1.-x); y*=y;
        z=Re(korifit76(x)); z*=z;
        t=y-z;
        u=-log(fabs(t))/log(10);
        printf("%6.2lf %19.16lf %19.16lf %19.16lf %8.2lf\n",x,y,z,t,u);
        if(n==1) M(x,u) else if(u>0 && u <20)L(x,u)
}
fprintf(o,"0 .7 0 RGB .1 W S\n");

for(n=1;n<5001;n+=5){ x=.01*n;
        y=j0(L1*sqrt(x))/(1.-x);
        z=Re(korifit76(x));
        t=y-z;
        u=-log(fabs(t))/log(10);
        printf("%6.2lf %19.16lf %19.16lf %19.16lf %8.2lf\n",x,y,z,t,u);
        if(n==1) M(x,u) else if(u>0 && u <20)L(x,u)
}
fprintf(o,"1 0 0 RGB .1 W S\n");

for(n=1;n<5001;n+=5){ x=.01*n;
        y=j0(L1*sqrt(x))/(1.-x); y*=y;
        z=Re(korifit76(x)); z*=z;
        t=y-z;
        u=-log(fabs(t)/(fabs(y)+fabs(z)))/log(10);
        printf("%6.2lf %19.16lf %19.16lf %19.16lf %8.2lf\n",x,y,z,t,u);
        if(n==1) M(x,u) else if(u>0 && u <20)L(x,u)
}
fprintf(o,"0 0 0 RGB .1 W S\n");

for(n=1;n<5001;n+=5){ x=.01*n;
        y=j0(L1*sqrt(x))/(1.-x);
        if(n==1) M(x,10*y) else if(y>-1 && y <2)L(x,10*y) }
fprintf(o,"1 0 0 RGB .1 W S\n");

for(n=1;n<5001;n+=5){ x=.01*n;
        y=j0(L1*sqrt(x))/(1.-x); y*=y;
        if(n==1) M(x,10*y) else if(y>-1 && y <2)L(x,10*y) }
fprintf(o,"0 .6 0 RGB .1 W S\n");

fprintf(o,"showpage\n%c%cTrailer\n",'%','%'); fclose(o);
system("epstopdf norifit76plo.eps");
system( "open norifit76plo.pdf");
return 0;}


Latex generator of labels


\documentclass[12pt]{article}
\usepackage{geometry}
\usepackage{graphics}
\usepackage{rotating}
\paperwidth 516pt
\paperheight 216pt
\textwidth 420pt
\textheight 300pt
\topmargin -108pt
\oddsidemargin -73pt
\newcommand \ds {\displaystyle}
\newcommand \sx {\scalebox}
\newcommand \rme {\mathrm{e}}
\newcommand \rot {\begin{rotate}}
\newcommand \ero {\end{rotate}}
\newcommand \ing {\includegraphics}
\pagestyle{empty}
\parindent 0pt
\begin{document}
%\begin{picture}(410,126)
\begin{picture}(614,212)
%\put(0,0){\ing{moriplo}}
%\put(0,0){\ing{23}}
%\put(0,0){\ing{korifit76plo}}
\put(4,0){\ing{norifit76plo}}
\put(6,200){\sx{1.1}{$y$}}
\put(0,156){\sx{1.1}{$15$}}
\put(0,106){\sx{1.1}{$10$}}
\put(0, 56){\sx{1.1}{$~5$}}
\put(0, 6){\sx{1.1}{$~0$}}
\put(11,-1){\sx{1.1}{$0$}}
%\put(43,-2){\sx{1.}{$(L_2/L_1)^2$}}
\put(60,0){\sx{1.}{$M_2$}}
\put(107,-1){\sx{1.1}{$10$}}
\put(137,0){\sx{1.}{$M_3$}}
%\put(159,-1){\sx{1.1}{$15$}}
\put(208,-1){\sx{1.1}{$20$}}
\put(248,0){\sx{1.}{$M_4$}}
\put(309,-1){\sx{1.1}{$30$}}
\put(393,0){\sx{1.}{$M_5$}}
\put(410,-2){\sx{1.1}{$40$}}
\put(509,-2){\sx{1.1}{$x$}}
\put(24,82){\rot{-65}\sx{.9}{$y\!=\! 10\, \mathrm{kori}(x)$}\ero}
\put(12,52){\rot{-65}\sx{.9}{$y\!=\! 10 \mathrm{nori}(x)$}\ero}
%
\put(440,162){\rot{-20}\sx{1.1}{$y\!=\! \mathrm{agreeA}(x)$}\ero}
\put(432,132){\rot{-25}\sx{1.1}{$y\!=\! \mathrm{agreeB}(x)$}\ero}
\put(426,110){\rot{-25}\sx{1.1}{$y\!=\! \mathrm{agreeC}(x)$}\ero}
%\put(576,60){\rot{-16}\sx{1.3}{$y\!=\! 10 \mathrm{agreeC}(x)}(x)$}\ero}
\end{picture}\end{document}

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current06:13, 1 December 2018Thumbnail for version as of 06:13, 1 December 2018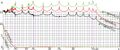1,070 × 448 (168 KB)Maintenance script (talk | contribs)Importing image file

You cannot overwrite this file.

The following page uses this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://mizugadro.mydns.jp/t/index.php?title=File:Norifit76plot.jpg&oldid=20463"