Difference between revisions of "ArcCosqq"
m (Text replacement - "\$([^\$]+)\$" to "\\(\1\\)") |
|||
| Line 1: | Line 1: | ||
[[File:AcosqqplotT.png|right|300px]] |
[[File:AcosqqplotT.png|right|300px]] |
||
'''ArcCosqq''' is holomorphic function defined with |
'''ArcCosqq''' is holomorphic function defined with |
||
| − | : |
+ | : \(\text{acosqq}(z)=\text{acosq}(z)\, \tan\!\!\big( \text{acosq}(z) \big)\) |
through functions [[acosq]] (or [[ArcCosq]]) expressed with |
through functions [[acosq]] (or [[ArcCosq]]) expressed with |
||
| − | : |
+ | : \(\text{acosq}(z)=\text{acosq}\big( \mathrm e ^{\mathrm i \pi /4}\, z \big)\) |
| − | which is [[ArcCosc]] of argument rotated for the phase '''q'''uarter of |
+ | which is [[ArcCosc]] of argument rotated for the phase '''q'''uarter of \(\pi\). Namely this phase appears in the application for the [[atom optics]], for [[channelling of particle between absorbing walls]]. |
[[acosc]] or [[ArcCosc]] is inverse function of [[cosc]], |
[[acosc]] or [[ArcCosc]] is inverse function of [[cosc]], |
||
| − | : |
+ | : \(\displaystyle \text{cosc}(z)=\frac{\cos(z)}{z}\) |
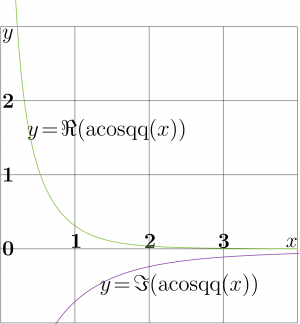
Graphic of the real part and that of the imaginary part of the function [[ArcCosqq]] of real argument are shown in the figure. |
Graphic of the real part and that of the imaginary part of the function [[ArcCosqq]] of real argument are shown in the figure. |
||
| − | While the argument approaches zero, functions [[ArcCosc]] and [[ArcCosq]] approach |
+ | While the argument approaches zero, functions [[ArcCosc]] and [[ArcCosq]] approach \(\pi/2\), and the [[Tangent]] in definition of [[ArcCosqq]] provides the singularity; so, the real part at zero becomes infinite. |
==Application== |
==Application== |
||
Latest revision as of 18:26, 30 July 2019
ArcCosqq is holomorphic function defined with
- \(\text{acosqq}(z)=\text{acosq}(z)\, \tan\!\!\big( \text{acosq}(z) \big)\)
through functions acosq (or ArcCosq) expressed with
- \(\text{acosq}(z)=\text{acosq}\big( \mathrm e ^{\mathrm i \pi /4}\, z \big)\)
which is ArcCosc of argument rotated for the phase quarter of \(\pi\). Namely this phase appears in the application for the atom optics, for channelling of particle between absorbing walls.
acosc or ArcCosc is inverse function of cosc,
- \(\displaystyle \text{cosc}(z)=\frac{\cos(z)}{z}\)
Graphic of the real part and that of the imaginary part of the function ArcCosqq of real argument are shown in the figure. While the argument approaches zero, functions ArcCosc and ArcCosq approach \(\pi/2\), and the Tangent in definition of ArcCosqq provides the singularity; so, the real part at zero becomes infinite.
Application
Function ArcCosqq expresses the decay of the atomic mode outside the channel, while function ArcCosq expresses the transversal wavenumber of this mode inside the channel. The argument of these functions has sense of the normalized damping of the atomic wave in the absorbing region.
Keywords
ArcCosc, Channeling of waves by absorbing walls, Makoto Morinaga