Difference between revisions of "File:AcosqqplotT.png"
(Importing image file) |
|||
| Line 1: | Line 1: | ||
| + | Graphic of function [[ArcCosqq]] (or acosqq) defined with |
||
| − | Importing image file |
||
| + | : $\text{acosqq}(z)=\text{acosq}(z)\, \tan\!\!\big( \text{acosq}(z) \big)$ |
||
| + | through functions [[acosq]] (or [[ArcCosq]]); it is expressed as; |
||
| + | : $\text{acosq}(z)=\text{acosq}\big( \mathrm e ^{\mathrm i \pi /4}\, z \big)$ |
||
| + | which is [[ArcCosc]] of argument rotated for the phase '''q'''uarter of $\pi$. Namely this phase appear in the application for the [[atom optics]], |
||
| + | for [[channelling of particle between absorbing walls]]. |
||
| + | |||
| + | [[acosc]] or [[ArcCosc]] is inverse funciotn of [[cosc]], |
||
| + | : $\displaystyle \text{cosc}(z)=\frac{\cos(z)}{z}$ |
||
| + | |||
| + | ==Use of function acosqq== |
||
| + | [[acoscqq]] expresses the decay constant of mode guided between absorbing waves, see the special article |
||
| + | [[Absorbing Schroedinger]] for the details. |
||
| + | |||
| + | ==C++ generator of curves== |
||
| + | Files [[ado.cin]] and [[acosc.cin]] should be loaded into the working directory in order to compile the [[C++]] |
||
| + | |||
| + | #include <math.h> |
||
| + | #include <stdio.h> |
||
| + | #include <stdlib.h> |
||
| + | #define DB double |
||
| + | #define DO(x,y) for(x=0;x<y;x++) |
||
| + | using namespace std; |
||
| + | #include <complex> |
||
| + | typedef complex<double> z_type; |
||
| + | #define Re(x) x.real() |
||
| + | #define Im(x) x.imag() |
||
| + | #define I z_type(0.,1.) |
||
| + | |||
| + | #include "ado.cin" |
||
| + | |||
| + | #include "acosc.cin" |
||
| + | |||
| + | z_type acosq(z_type z){ z_type c=z*exp(I*M_PI/4.); c=acosc(c); return c;} |
||
| + | |||
| + | z_type acosqq(z_type z){ z_type c=z*exp(I*M_PI/4.); c=acosc(c); return c*tan(c);} |
||
| + | |||
| + | #define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y); |
||
| + | #define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y); |
||
| + | #define S(x,y) fprintf(o,"S\n",); |
||
| + | main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d; |
||
| + | DB Sazae= 2.798386045783887; // H |
||
| + | DB Tarao= -0.33650841691839534; // J |
||
| + | FILE *o;o=fopen("acosqqplot.eps","w");ado(o,420,460); |
||
| + | fprintf(o,"10 110 translate\n 100 100 scale\n"); |
||
| + | for(m=0;m<5;m++){M(m,-1)L(m,3)} |
||
| + | for(n=-1;n<4;n++){M(0,n)L(4,n)} |
||
| + | fprintf(o,"2 setlinecap .005 W 0 0 0 RGB S\n"); |
||
| + | /* |
||
| + | for(m=-4;m<3;m++){M(.5+m,-1)L(.5+m,3)} |
||
| + | for(n=-1;n<3;n++){M(-4,n+.5)L(4,n+.5)} |
||
| + | fprintf(o,"2 setlinecap .003 W 0 0 0 RGB S\n"); |
||
| + | */ |
||
| + | DO(m,381){x=0.198+.01*m; y=Re(acosqq(x)); if(m==0)M(x,y)else L(x,y); |
||
| + | printf("%6.3f %6.3f\n",x,y); } |
||
| + | fprintf(o,"1 setlinejoin 1 setlinecap .011 W 0 .6 0 RGB S\n"); |
||
| + | DO(m,330){x=0.73+.01*m; y=Im(acosqq(x)); if(m==0)M(x,y)else L(x,y) } |
||
| + | fprintf(o,"1 setlinejoin 1 setlinecap .01 W .7 0 .7 RGB S\n"); |
||
| + | // M(-.1,M_PI/2)L( .1,M_PI/2) fprintf(o,".004 W 0 0 0 RGB S\n"); |
||
| + | fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o); |
||
| + | system("epstopdf acosqqplot.eps"); |
||
| + | system( "open acosqqplot.pdf"); |
||
| + | getchar(); system("killall Preview");//for mac |
||
| + | } |
||
| + | |||
| + | ==Latex generator of labels== |
||
| + | File [[acosqqplot.pdf]] should be generated with the code above in order to compile the [[Latex]] document below. |
||
| + | |||
| + | %<nowiki><br> |
||
| + | % Copyleft 2012 by Dmitrii Kouznetsov %<br> |
||
| + | \documentclass[12pt]{article} %<br> |
||
| + | \usepackage{geometry} %<br> |
||
| + | \usepackage{graphicx} %<br> |
||
| + | \usepackage{rotating} %<br> |
||
| + | \paperwidth 812pt %<br> |
||
| + | \paperheight 878pt %<br> |
||
| + | \topmargin -90pt %<br> |
||
| + | \oddsidemargin -106pt %<br> |
||
| + | \textwidth 900pt %<br> |
||
| + | \textheight 900pt %<br> |
||
| + | \pagestyle {empty} %<br> |
||
| + | \newcommand \sx {\scalebox} %<br> |
||
| + | \newcommand \rot {\begin{rotate}} %<br> |
||
| + | \newcommand \ero {\end{rotate}} %<br> |
||
| + | \newcommand \ing {\includegraphics} %<br> |
||
| + | \begin{document} %<br> |
||
| + | \parindent 0pt |
||
| + | \sx{2}{ \begin{picture}(140,444) %<br> |
||
| + | %\put(4,6){\ing{sazaecon}} %<br> |
||
| + | \put(16,402){\sx{2.5}{$y$}} %<br> |
||
| + | \put(16,308){\sx{2.4}{\bf 2}} %<br> |
||
| + | %\put(422,269){\sx{2.4}{$\pi/2$}} %<br> |
||
| + | \put(16,208){\sx{2.4}{\bf 1}} %<br> |
||
| + | %\put(16, 262){\sx{2.2}{Wakame}} %<br> |
||
| + | \put(16,108){\sx{2.4}{\bf 0}} %<br> |
||
| + | %\put(16, 75){\sx{2.4}{Tarao}} %<br> |
||
| + | %\put(200, 118){\sx{2.4}{\bf -2}} %<br> |
||
| + | %\put(300, 118){\sx{2.4}{\bf -1}} %<br> |
||
| + | \put(108, 118){\sx{2.4}{\bf 1}} %<br> |
||
| + | %\put(142,120){\sx{2.4}{\rot{90}Fune\ero}} %<br> |
||
| + | \put(208, 118){\sx{2.4}{\bf 2}} %<br> |
||
| + | %\put(302,118){\sx{2.5}{\rot{90}Sazae\ero}} %<br> |
||
| + | \put(308, 118){\sx{2.4}{\bf 3}} %<br> |
||
| + | %\put(807, 120){\sx{2.2}{\bf 4}} %<br> |
||
| + | %\put(161, 132){\sx{2.8}{$\frac{\pi}{2}$}} %<br> |
||
| + | %\put(471, 130){\sx{2.6}{$\frac{3\pi}{2}$}} %<br> |
||
| + | \put(400, 119){\sx{2.4}{$x$}} %<br> |
||
| + | \put(4,6){\ing{acosqqplot}} %<br> |
||
| + | \put(50,270){\sx{2.52}{\rot{0}$y\!=\!\Re(\mathrm{acosqq}(x))$\ero}} %<br> |
||
| + | \put(148, 60){\sx{2.52}{\rot{0}$y\!=\!\Im(\mathrm{acosqq}(x))$\ero}} %<br> |
||
| + | \end{picture} %<br> |
||
| + | } %<br> |
||
| + | \end{document} |
||
| + | %</nowiki> |
||
| + | |||
| + | [[Category:ArcCosqq]] |
||
| + | [[Category:ArcCosq]] |
||
| + | [[Category:ArcCosc]] |
||
| + | [[Category:Explicit plot]] |
||
| + | [[Category:C++]] |
||
| + | [[Category:Latex]] |
||
| + | [[Category:Guiding of waves between absorbing walls]] |
||
Latest revision as of 09:41, 21 June 2013
Graphic of function ArcCosqq (or acosqq) defined with
- $\text{acosqq}(z)=\text{acosq}(z)\, \tan\!\!\big( \text{acosq}(z) \big)$
through functions acosq (or ArcCosq); it is expressed as;
- $\text{acosq}(z)=\text{acosq}\big( \mathrm e ^{\mathrm i \pi /4}\, z \big)$
which is ArcCosc of argument rotated for the phase quarter of $\pi$. Namely this phase appear in the application for the atom optics, for channelling of particle between absorbing walls.
acosc or ArcCosc is inverse funciotn of cosc,
- $\displaystyle \text{cosc}(z)=\frac{\cos(z)}{z}$
Use of function acosqq
acoscqq expresses the decay constant of mode guided between absorbing waves, see the special article Absorbing Schroedinger for the details.
C++ generator of curves
Files ado.cin and acosc.cin should be loaded into the working directory in order to compile the C++
#include <math.h> #include <stdio.h> #include <stdlib.h> #define DB double #define DO(x,y) for(x=0;x<y;x++) using namespace std; #include <complex> typedef complex<double> z_type; #define Re(x) x.real() #define Im(x) x.imag() #define I z_type(0.,1.)
#include "ado.cin"
#include "acosc.cin"
z_type acosq(z_type z){ z_type c=z*exp(I*M_PI/4.); c=acosc(c); return c;}
z_type acosqq(z_type z){ z_type c=z*exp(I*M_PI/4.); c=acosc(c); return c*tan(c);}
#define M(x,y) fprintf(o,"%6.4f %6.4f M\n",0.+x,0.+y);
#define L(x,y) fprintf(o,"%6.4f %6.4f L\n",0.+x,0.+y);
#define S(x,y) fprintf(o,"S\n",);
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d;
DB Sazae= 2.798386045783887; // H
DB Tarao= -0.33650841691839534; // J
FILE *o;o=fopen("acosqqplot.eps","w");ado(o,420,460);
fprintf(o,"10 110 translate\n 100 100 scale\n");
for(m=0;m<5;m++){M(m,-1)L(m,3)}
for(n=-1;n<4;n++){M(0,n)L(4,n)}
fprintf(o,"2 setlinecap .005 W 0 0 0 RGB S\n");
/*
for(m=-4;m<3;m++){M(.5+m,-1)L(.5+m,3)}
for(n=-1;n<3;n++){M(-4,n+.5)L(4,n+.5)}
fprintf(o,"2 setlinecap .003 W 0 0 0 RGB S\n");
*/
DO(m,381){x=0.198+.01*m; y=Re(acosqq(x)); if(m==0)M(x,y)else L(x,y);
printf("%6.3f %6.3f\n",x,y); }
fprintf(o,"1 setlinejoin 1 setlinecap .011 W 0 .6 0 RGB S\n");
DO(m,330){x=0.73+.01*m; y=Im(acosqq(x)); if(m==0)M(x,y)else L(x,y) }
fprintf(o,"1 setlinejoin 1 setlinecap .01 W .7 0 .7 RGB S\n");
// M(-.1,M_PI/2)L( .1,M_PI/2) fprintf(o,".004 W 0 0 0 RGB S\n");
fprintf(o,"showpage\n%c%cTrailer",'%','%'); fclose(o);
system("epstopdf acosqqplot.eps");
system( "open acosqqplot.pdf");
getchar(); system("killall Preview");//for mac
}
Latex generator of labels
File acosqqplot.pdf should be generated with the code above in order to compile the Latex document below.
%<br> % Copyleft 2012 by Dmitrii Kouznetsov %<br> \documentclass[12pt]{article} %<br> \usepackage{geometry} %<br> \usepackage{graphicx} %<br> \usepackage{rotating} %<br> \paperwidth 812pt %<br> \paperheight 878pt %<br> \topmargin -90pt %<br> \oddsidemargin -106pt %<br> \textwidth 900pt %<br> \textheight 900pt %<br> \pagestyle {empty} %<br> \newcommand \sx {\scalebox} %<br> \newcommand \rot {\begin{rotate}} %<br> \newcommand \ero {\end{rotate}} %<br> \newcommand \ing {\includegraphics} %<br> \begin{document} %<br> \parindent 0pt \sx{2}{ \begin{picture}(140,444) %<br> %\put(4,6){\ing{sazaecon}} %<br> \put(16,402){\sx{2.5}{$y$}} %<br> \put(16,308){\sx{2.4}{\bf 2}} %<br> %\put(422,269){\sx{2.4}{$\pi/2$}} %<br> \put(16,208){\sx{2.4}{\bf 1}} %<br> %\put(16, 262){\sx{2.2}{Wakame}} %<br> \put(16,108){\sx{2.4}{\bf 0}} %<br> %\put(16, 75){\sx{2.4}{Tarao}} %<br> %\put(200, 118){\sx{2.4}{\bf -2}} %<br> %\put(300, 118){\sx{2.4}{\bf -1}} %<br> \put(108, 118){\sx{2.4}{\bf 1}} %<br> %\put(142,120){\sx{2.4}{\rot{90}Fune\ero}} %<br> \put(208, 118){\sx{2.4}{\bf 2}} %<br> %\put(302,118){\sx{2.5}{\rot{90}Sazae\ero}} %<br> \put(308, 118){\sx{2.4}{\bf 3}} %<br> %\put(807, 120){\sx{2.2}{\bf 4}} %<br> %\put(161, 132){\sx{2.8}{$\frac{\pi}{2}$}} %<br> %\put(471, 130){\sx{2.6}{$\frac{3\pi}{2}$}} %<br> \put(400, 119){\sx{2.4}{$x$}} %<br> \put(4,6){\ing{acosqqplot}} %<br> \put(50,270){\sx{2.52}{\rot{0}$y\!=\!\Re(\mathrm{acosqq}(x))$\ero}} %<br> \put(148, 60){\sx{2.52}{\rot{0}$y\!=\!\Im(\mathrm{acosqq}(x))$\ero}} %<br> \end{picture} %<br> } %<br> \end{document} %
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 17:50, 20 June 2013 | 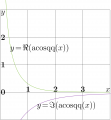 | 1,686 × 1,823 (148 KB) | Maintenance script (talk | contribs) | Importing image file |
You cannot overwrite this file.
File usage
The following page uses this file: