Search results
Create the page "Mathematics of computation" on this wiki! See also the search results found.
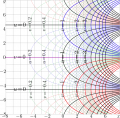
File:ExpQ2mapT.png [[Complex map]] of [[exponential]] to [[base sqrt2]], id est, $b=\sqrt{2}$; ...ion to base sqrt(2)]] in the illustration of the application of the method of [[regular iteration]] to construct the [[superfunction]](1,765 × 1,729 (1.15 MB)) - 08:35, 1 December 2018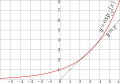
File:ExpQ2plotT.png [[Explicit plot]] of [[exponential]] to base $b\!=\!\sqrt{2} \approx 1.414213562373095$ The [[fixed point]]s $L\!=\!2$ and $L\!=\!4$ are solutions of the equation(2,512 × 1,744 (175 KB)) - 08:35, 1 December 2018
File:Filogbigmap100.png [[File:Filogmap300.png|right|300px|thumb|The zoom-in of the central part of the map]] [[Complex map]] of function [[Filog]].(2,870 × 2,851 (847 KB)) - 08:36, 1 December 2018
File:Filogmap300.png [[Complex map]] of function [[Filog]]. ==Semantics of Filog==(893 × 897 (292 KB)) - 09:40, 21 June 2013
File:IterEq2plotU.png ...f [[exponential]] to [[base sqrt(2)]] for various values of the number $c$ of iterations. ...ion, the plotter uses the implementation through the [[superfunction]] $F$ of the exponential to base $\sqrt{2}$, constructed at the fixed point $L\!=\!4(2,944 × 2,944 (986 KB)) - 21:42, 27 September 2013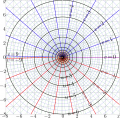
File:LogQ2mapT2.png [[Complex map]] of [[logarithm]] to base $b\!=\!\sqrt{2}$; The cut of the range of holomorphism is marked with dashed line. Lines $u\!=\!1$, $u\!=\!2$, $u\!=\(1,765 × 1,729 (1.43 MB)) - 09:43, 21 June 2013
File:SqrtExpZ.jpg [[Complex map]]s of function <math>f=\exp^c(z)</math> in the <math>z</math> plane for some real values of <math>c=\pm 1, \pm 0.9, \pm 0.5, \pm 0.1</math>.(842 × 953 (83 KB)) - 11:56, 21 June 2013
File:Sqrt2figf45bT.png [[Complex map]] of the primary expansion of the growing [[superexponential]] to base $b\!=\!\sqrt{2}$ built up at the [ :$a_0=L=4$ is fixed point of the exponential transfer function $T$,(2,180 × 2,159 (1.01 MB)) - 08:52, 1 December 2018
File:Sqrt2figf45eT.png [[Complex map]] of the real-holomorphic [[superfunction]] $F$ of the [[exponential]] to base $b\!=\!\sqrt{2}$ built up at its fixed point $L ...is almost Figure 2 (left at the bottom) of publication in [[Mathematics of Computation]](2,180 × 2,159 (1.18 MB)) - 08:52, 1 December 2018
File:Sqrt2figL45eT.png [[Complex map]] of the [[Abel function]] $G$ of the [[exponential]] to base $b\!=\!\sqrt{2}$ constructed at the fixed point In the [[Mathematics of computation]](2,180 × 2,159 (1.07 MB)) - 12:53, 20 July 2020
File:TetSheldonImaT.png The holomorphic solution $F$ of equation where [[Filog]] is [[fixed point]] of the [[logarithm]].(4,359 × 980 (598 KB)) - 09:40, 21 June 2013- ...e [[complex map]]s of [[tetration]] \(\mathrm{tet}_b\) to different values of base \(b\). For real values of base \(b\), the real-real plots \(y\!=\!\mathrm{tet}_b(x)\) are shown in th5 KB (761 words) - 12:00, 21 July 2020
- ...2009). Solutions of F(z+1)=exp(F(z)) in the complex plane.. Mathematics of Computation, 78: 1647-1670. While Russian version of that article, id est, [[Тетрация]] is not loaded, the English vers16 KB (821 words) - 14:42, 21 July 2020
- ...function \(f(z)=\exp^n(z)\), where upper superscript indicates the number of iteration. ...the number in superscript after a name of any function denotes the number of iteration. This notation is neither new, nor original;7 KB (1,161 words) - 18:43, 30 July 2019
- [[Iterate_of_linear_fraction]] (or [[iteration of linnet friaction]]) refers to function [[Iterate]] of a [[linear fraction]] can be expressed with also some linear fraction. This13 KB (2,088 words) - 06:43, 20 July 2020
- ...of [[abelfunction]]s, [[superfunction]]s, and the non-integer [[iterate]]s of holomorphic functions. In particular, results for [[tetration]], [[arctetration]] and [[iterate]]s of [[exponential]] are presented.15 KB (2,166 words) - 20:33, 16 July 2023

File:IterEq2plotT.jpg ...f [[exponential]] to [[base sqrt(2)]] for various values of the number $c$ of iterations. ...ion, the plotter uses the implementation through the [[superfunction]] $F$ of the exponential to base $\sqrt{2}$, constructed at the fixed point $L\!=\!4(2,922 × 2,922 (1.35 MB)) - 08:38, 1 December 2018
File:Ack3a600.jpg [[Complex map]] of [[tetration]] to base $b\!=\!\sqrt{2}\!\approx\!1.41$ ==[[C++]] Generator of map]==(5,130 × 1,793 (1.09 MB)) - 08:28, 1 December 2018
File:Ack3b600.jpg [[Complex map]] of [[tetration]] to base $b\!=\!\exp(1/\mathrm e)\!\approx\!1.44$ ==[[C++]] Generator of map]==(5,130 × 1,776 (1 MB)) - 08:28, 1 December 2018
File:Ack3c600.jpg [[Complex map]] of [[tetration]] to base $b\!=\!3/2\!=1.5$ ==[[C++]] Generator of map]==(5,130 × 1,776 (1.5 MB)) - 08:28, 1 December 2018